
2.复数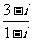 等于( ).
等于( ).
A. B.
B. C.
C. D.
D.
1.集合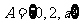 ,
, ,若
,若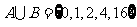 ,则
,则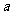 的值为( )
的值为( )
A.0 B.1 C.2 D.4
[解析]:∵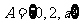 ,
, ,
,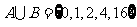 ∴
∴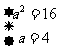 ∴
∴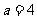 ,故选D.
,故选D.
答案:D
[命题立意]:本题考查了集合的并集运算,并用观察法得到相对应的元素,从而求得答案,本题属于容易题.
21、解:(I)已知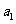 是奇数,假设
是奇数,假设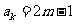 是奇数,其中
是奇数,其中 为正整数,
为正整数,
则由递推关系得 是奇数。
是奇数。 

根据数学归纳法,对任何 ,
,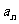 都是奇数。
都是奇数。
(II)(方法一)由 知,
知,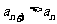 当且仅当
当且仅当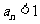 或
或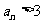 。
。
另一方面,若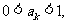 则
则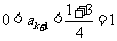 ;若
;若 ,则
,则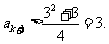
根据数学归纳法,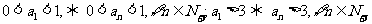
综合所述,对一切 都有
都有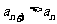 的充要条件是
的充要条件是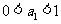 或
或 。
。
(方法二)由 得
得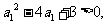 于是
于是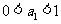 或
或 。
。



因为 所以所有的
所以所有的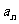 均大于0,因此
均大于0,因此 与
与 同号。
同号。
根据数学归纳法, ,
, 与
与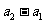 同号。
同号。
因此,对一切 都有
都有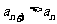 的充要条件是
的充要条件是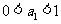 或
或 。
。


20、解:本小题主要考查直线和椭圆的标准方程和参数方程,直线和曲线的几何性质,等比数列等基础知识。考查综合运用知识分析问题、解决问题的能力。本小题满分13分。
解:(I)(方法一)由 得
得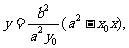 代入椭圆
代入椭圆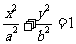 ,
,
得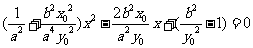 .
.
将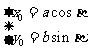 代入上式,得
代入上式,得 从而
从而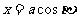
因此,方程组 有唯一解
有唯一解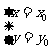 ,即直线
,即直线 与椭圆有唯一交点P.
与椭圆有唯一交点P. 

(方法二)显然P是椭圆与 的交点,若Q
的交点,若Q 是椭圆与
是椭圆与 的交点,代入
的交点,代入 的方程
的方程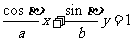 ,得
,得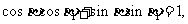
即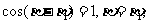 故P与Q重合。
故P与Q重合。
(方法三)在第一象限内,由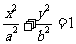 可得
可得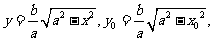
椭圆在点P处的切线斜率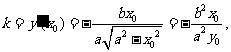
切线方程为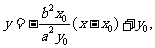 即
即 。
。
因此, 就是椭圆在点P处的切线。
就是椭圆在点P处的切线。
根据椭圆切线的性质,P是椭圆与直线 的唯一交点。
的唯一交点。
(II)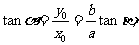
 的斜率为
的斜率为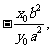
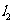 的斜率为
的斜率为
由此得
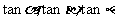 构成等比数列。
构成等比数列。
19、解: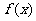 的定义域是(0,+
的定义域是(0,+ ),
),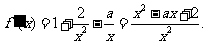
设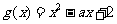 ,二次方程
,二次方程 的判别式
的判别式 .
.
①
当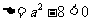 ,即
,即 时,对一切
时,对一切 都有
都有 ,此时
,此时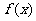 在
在 上是增函数。
上是增函数。
②
当 ,即
,即 时,仅对
时,仅对 有
有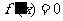 ,对其余的
,对其余的 都有
都有 ,此时
,此时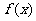 在
在 上也是增函数。
上也是增函数。
③
当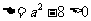 ,即
,即 时,
时, 

方程 有两个不同的实根
有两个不同的实根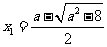 ,
,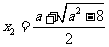 ,
,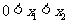 .
.
 |
 |
 |
 |
 |
 |
 |
+ |
0 |
_ |
0 |
+ |
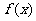 |
单调递增 |
极大 |
单调递减 |
极小 |
单调递增 |
此时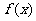 在
在 上单调递增, 在
上单调递增, 在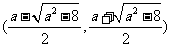 是上单调递减, 在
是上单调递减, 在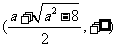 上单调递增.
上单调递增.
18、解:(I)(综合法)连接AC、BD交于菱形的中心O,过O作OG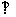 AF,
AF,
G为垂足。连接BG、DG。由BD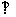 AC,BD
AC,BD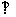 CF得BD
CF得BD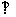 平面ACF,故BD
平面ACF,故BD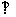 AF。
AF。
于是AF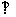 平面BGD,所以BG
平面BGD,所以BG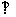 AF,DG
AF,DG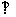 AF,
AF, BGD为二面角B-AF-D 的平面角。
BGD为二面角B-AF-D 的平面角。
由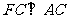 ,
, 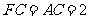 ,得
,得 ,
,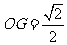
由 ,得
,得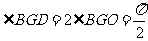


(向量法)以A为坐标原点,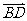 、
、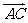 、
、 方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系(如图)
方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系(如图)
设平面ABF的法向量 ,则由
,则由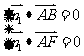 得
得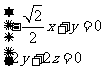
令 ,得
,得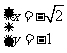 ,
,
同理,可求得平面ADF的法向量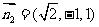 。
。 

由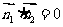 知,平面ABF与平面ADF垂直,
知,平面ABF与平面ADF垂直,
二面角B-AF-D的大小等于 。
。
(II)连EB、EC、ED,设直线AF与直线CE相交于点H,则四棱锥E-ABCD与四棱锥F-ABCD的公共部分为四棱锥H-ABCD。
过H作HP⊥平面ABCD,P为垂足。
因为EA⊥平面ABCD,FC⊥平面ABCD,,所以平面ACFE⊥平面ABCD,从而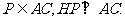
由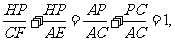 得
得 。
。
又因为
故四棱锥H-ABCD的体积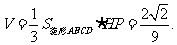


17、解:随机变量X的分布列是
|
X |
1 |
2 |
3 |
|
P |
 |
 |
 |
X的均值为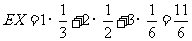


附:X的分布列的一种求法
共有如下6种不同的可能情形,每种情形发生的概率都是 :
:
|
① |
② |
③ |
④ |
⑤ |
⑥ |
|
A-B-C-D |
A-B-C └D |
A-B-C └D |
A-B-D └C |
A-C-D └B |
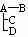 |
在情形①和②之下,A直接感染了一个人;在情形③、④、⑤之下,A直接感染了两个人;在情形⑥之下,A直接感染了三个人。
16、解:(Ⅰ)由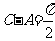 ,且
,且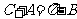 ,∴
,∴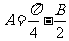 ,∴
,∴ ,
,
 ∴
∴ ,又
,又 ,∴
,∴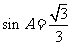
(Ⅱ)如图,由正弦定理得
∴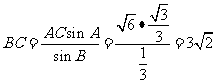 ,又
,又
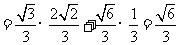
∴
15、[解析]①④⑤
14、[解析]设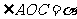
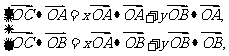 ,即
,即
∴
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com