
8.函数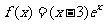 的单调递增区间是
的单调递增区间是
A.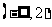 B.(0,3) C.(1,4) D.
B.(0,3) C.(1,4) D.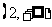
7.已知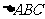 中,
中,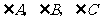 的对边分别为
的对边分别为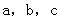 。若
。若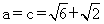 ,且
,且 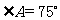 ,则
,则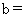
A.2
B.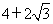 C.
C. 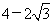 D.
D.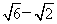
6.给定下列四个命题:
①若一个平面内的两条直线与另外一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直。
其中,为真命题的是
A.①和② B.②和③ C.③和④ D.②和④
5.已知等比数列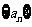 的公比为正数,且
的公比为正数,且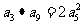 ,
,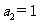 ,则
,则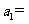
A.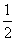 B.
B.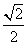 C.
C. 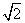 D.
D.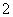
4.若函数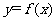 是函数
是函数 的反函数,且
的反函数,且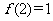 ,则
,则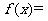
A.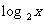 B.
B.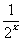 C.
C.
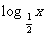 D.
D.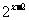
3.已知平面向量a =(x,1),b =(-x,x2 ),则向量a+b
A.平行于x轴 B.平行于第一、三象限的角平分线
C.平行于y轴 D.平行于第二、四象限的角平分线
2.下列n的取值中,使in =1(i是虚数单位)的是
A.n=2 B.n=3 C.n=4 D.n=5
1.已知全集U=R,则正确表示集合M={-1,0,1}和N={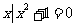 }关系的韦恩(Venn)图是
}关系的韦恩(Venn)图是

22. (本小题满分14分)
设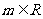 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量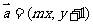 ,向量
,向量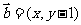 ,
,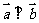 ,动点
,动点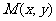 的轨迹为E.
的轨迹为E.
(1)求轨迹E的方程,并说明该方程所表示曲线的形状;
(2)已知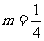 ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且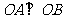 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;
(3)已知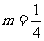 ,设直线
,设直线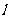 与圆C:
与圆C: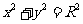 (1<R<2)相切于A1,且
(1<R<2)相切于A1,且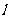 与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
解:(1)因为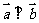 ,
,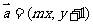 ,
,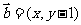 ,
,
所以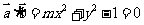 , 即
, 即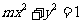 .
.
当m=0时,方程表示两直线,方程为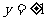 ;
;
当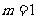 时, 方程表示的是圆
时, 方程表示的是圆
当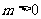 且
且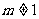 时,方程表示的是椭圆;
时,方程表示的是椭圆;
当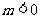 时,方程表示的是双曲线.
时,方程表示的是双曲线.
(2).当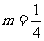 时, 轨迹E的方程为
时, 轨迹E的方程为 ,设圆心在原点的圆的一条切线为
,设圆心在原点的圆的一条切线为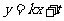 ,解方程组
,解方程组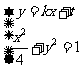 得
得 ,即
,即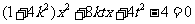 ,
,
要使切线与轨迹E恒有两个交点A,B,
则使△=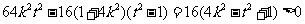 ,
,
即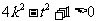 ,即
,即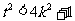 ,
且
,
且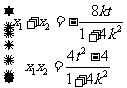
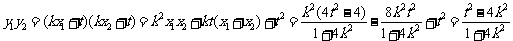 ,
,
要使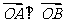 , 需使
, 需使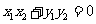 ,即
,即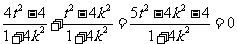 ,
,
所以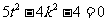 , 即
, 即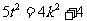 且
且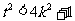 , 即
, 即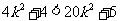 恒成立.
恒成立.
所以又因为直线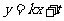 为圆心在原点的圆的一条切线,
为圆心在原点的圆的一条切线,
所以圆的半径为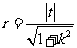 ,
,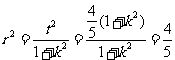 , 所求的圆为
, 所求的圆为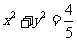 .
.
当切线的斜率不存在时,切线为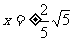 ,与
,与 交于点
交于点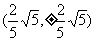 或
或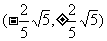 也满足
也满足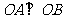 .
.
综上, 存在圆心在原点的圆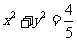 ,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且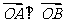 .
.
(3)当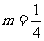 时,轨迹E的方程为
时,轨迹E的方程为 ,设直线
,设直线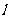 的方程为
的方程为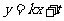 ,因为直线
,因为直线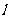 与圆C:
与圆C: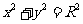 (1<R<2)相切于A1, 由(2)知
(1<R<2)相切于A1, 由(2)知 , 即
, 即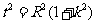 ①,
①,
因为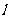 与轨迹E只有一个公共点B1,
与轨迹E只有一个公共点B1,
由(2)知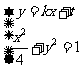 得
得 ,
,
即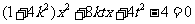 有唯一解
有唯一解
则△=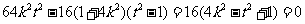 , 即
, 即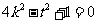 ,
②
,
②
由①②得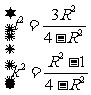 , 此时A,B重合为B1(x1,y1)点,
, 此时A,B重合为B1(x1,y1)点,
由 中
中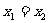 ,所以,
,所以, ,
,
B1(x1,y1)点在椭圆上,所以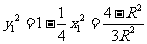 ,所以
,所以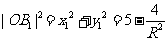 ,
,
在直角三角形OA1B1中,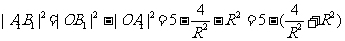 因为
因为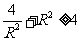 当且仅当
当且仅当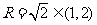 时取等号,所以
时取等号,所以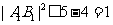 ,即
,即
当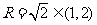 时|A1B1|取得最大值,最大值为1.
时|A1B1|取得最大值,最大值为1.
[命题立意]:本题主要考查了直线与圆的方程和位置关系,以及直线与椭圆的位置关系,可以通过解方程组法研究有没有交点问题,有几个交点的问题.
徐洪艳制作
21.(本小题满分12分)
已知函数 ,其中
,其中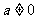


(1) 当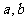 满足什么条件时,
满足什么条件时,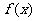 取得极值?
取得极值?
(2) 已知 ,且
,且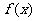 在区间
在区间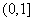 上单调递增,试用
上单调递增,试用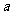 表示出
表示出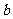 的取值范围.
的取值范围.
解: (1)由已知得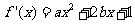 ,令
,令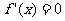 ,得
,得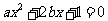 ,
,
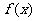 要取得极值,方程
要取得极值,方程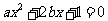 必须有解,
必须有解,
所以△ ,即
,即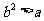 , 此时方程
, 此时方程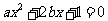 的根为
的根为
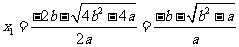 ,
,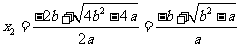 ,
,
所以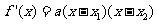


当 时,
时,
|
x |
(-∞,x1) |
x 1 |
(x1,x2) |
x2 |
(x2,+∞) |
|
f’(x) |
+ |
0 |
- |
0 |
+ |
|
f (x) |
增函数 |
极大值 |
减函数 |
极小值 |
增函数 |
所以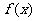 在x 1,
x2处分别取得极大值和极小值.
在x 1,
x2处分别取得极大值和极小值.
当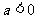 时,
时, 

|
x |
(-∞,x2) |
x 2 |
(x2,x1) |
x1 |
(x1,+∞) |
|
f’(x) |
- |
0 |
+ |
0 |
- |
|
f (x) |
减函数 |
极小值 |
增函数 |
极大值 |
减函数 |
所以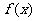 在x 1,
x2处分别取得极大值和极小值.
在x 1,
x2处分别取得极大值和极小值.
综上,当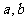 满足
满足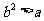 时,
时, 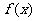 取得极值.
取得极值. 

(2)要使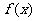 在区间
在区间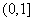 上单调递增,需使
上单调递增,需使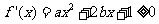 在
在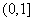 上恒成立.
上恒成立.
即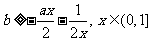 恒成立, 所以
恒成立, 所以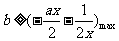
设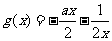 ,
, ,
,
令 得
得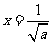 或
或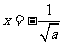 (舍去),
(舍去), 

当 时,
时,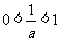 ,当
,当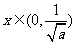 时
时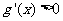 ,
,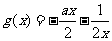 单调增函数;
单调增函数;
当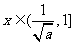 时
时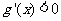 ,
,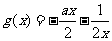 单调减函数,
单调减函数,
所以当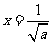 时,
时,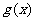 取得最大,最大值为
取得最大,最大值为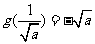 .
.
所以
当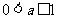 时,
时,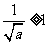 ,此时
,此时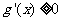 在区间
在区间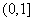 恒成立,所以
恒成立,所以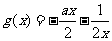 在区间
在区间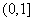 上单调递增,当
上单调递增,当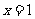 时
时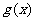 最大,最大值为
最大,最大值为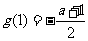 ,所以
,所以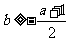
综上,当 时,
时,  ; 当
; 当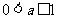 时,
时, 


[命题立意]:本题为三次函数,利用求导的方法研究函数的极值、单调性和函数的最值,函数在区间上为单调函数,则导函数在该区间上的符号确定,从而转为不等式恒成立,再转为函数研究最值.运用函数与方程的思想,化归思想和分类讨论的思想解答问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com