
7.”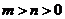 ”是”方程
”是”方程 表示焦点在y轴上的椭圆”的
表示焦点在y轴上的椭圆”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充要条件 (D) 既不充分也不必要条件
答案:C.
解析:将方程 转化为
转化为  , 根据椭圆的定义,要使焦点在y轴上必须满足
, 根据椭圆的定义,要使焦点在y轴上必须满足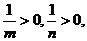 所以
所以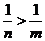 ,故选C.
,故选C. 
6.若 ,则
,则 的值为
的值为
(A)2 (B)0 (C)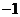 (D)
(D) 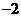
答案:C.
解析:由题意容易发现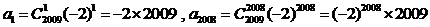 ,则
,则
 , 同理可以得出
, 同理可以得出 ,
,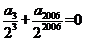 ………
………

亦即前2008项和为0, 则原式= =
=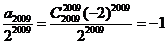 故选C.
故选C.
5.某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为 
(A)9 (B)18 (C)27 (D) 36
答案B.
解析:由比例可得该单位老年职工共有90人,用分层抽样的比例应抽取18人.
4.过原点且倾斜角为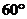 的直线被圆学
的直线被圆学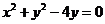 所截得的弦长为科网
所截得的弦长为科网
(A) (B)2
(C)
(B)2
(C) (D)2
(D)2
答案:D.
解析: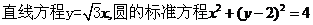 ,圆心
,圆心 到直线的距离
到直线的距离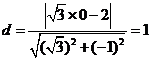 ,由垂径定理知所求弦长为
,由垂径定理知所求弦长为 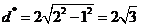 故选D.
故选D.
3.函数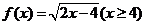 的反函数为
的反函数为
(A) (B)
(B) 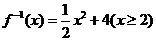
(C)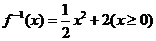 (D)学科
(D)学科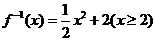
答案:D.

2.若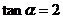 ,则
,则 的值为
的值为
(A)0 (B) 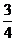 (C)1 (D)
(C)1 (D) 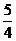
答案:B.
解析: 利用齐次分式的意义将分子分母同时除以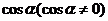 得,
得,
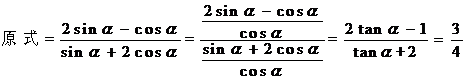 故选B.
故选B.
1.设不等式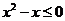 的解集为M,函数
的解集为M,函数 的定义域为N,则
的定义域为N,则 为
为
(A)[0,1) (B)(0,1) (C)[0,1] (D)(-1,0]
答案:A.
解析: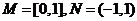 ,则
,则 ,故选A.
,故选A.
21.(本小题满分13分)
对于数列 ,若存在常数M>0,对任意的
,若存在常数M>0,对任意的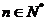 ,恒有
,恒有
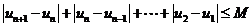 ,
, 

则称数列 为
为 数列.
数列.
(Ⅰ)首项为1,公比为 的等比数列是否为B-数列?请说明理由;
的等比数列是否为B-数列?请说明理由;
(Ⅱ)设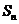 是数列
是数列 的前n项和.给出下列两组判断:
的前n项和.给出下列两组判断:
A组:①数列 是B-数列, ②数列
是B-数列, ②数列 不是B-数列;
不是B-数列;
B组:③数列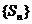 是B-数列, ④数列
是B-数列, ④数列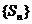 不是B-数列.
不是B-数列.
请以其中一组中的一个论断为条件,另一组中的一个论断为结论组成一个命题.
判断所给命题的真假,并证明你的结论;
(Ⅲ)若数列 是B-数列,证明:数列
是B-数列,证明:数列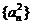 也是B-数列。
也是B-数列。
解: (Ⅰ)设满足题设的等比数列为 ,则
,则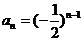 .于是
.于是
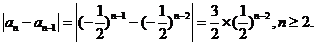



=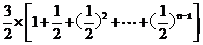 =
=
所以首项为1,公比为 的等比数列是B-数列 .
的等比数列是B-数列 .
(Ⅱ)命题1:若数列 是B-数列,则数列
是B-数列,则数列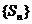 是B-数列.此命题为假命题.
是B-数列.此命题为假命题.
事实上设 =1,
=1,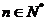 ,易知数列
,易知数列 是B-数列,但
是B-数列,但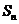 =n,
=n,
 .
.
由n的任意性知,数列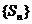 不是B-数列。
不是B-数列。
命题2:若数列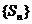 是B-数列,则数列
是B-数列,则数列 不是B-数列。此命题为真命题。
不是B-数列。此命题为真命题。
事实上,因为数列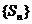 是B-数列,所以存在正数M,对任意的
是B-数列,所以存在正数M,对任意的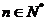 ,有
,有
 ,
,
即 .于是
.于是
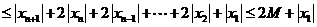 ,
,
所以数列 是B-数列。
是B-数列。
(注:按题中要求组成其它命题解答时,仿上述解法) 

(Ⅲ)若数列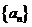 是B-数列,则存在正数M,对任意的
是B-数列,则存在正数M,对任意的 有
有
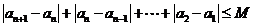 .
.
因为
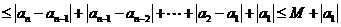 .
.
记 ,则有
,则有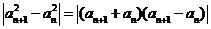
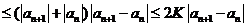 .
.
因此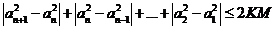 .
.
故数列 是B-数列.
是B-数列.


20.(本小题满分13分)
已知椭圆C的中心在原点,焦点在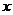 轴上,以两个焦点和短轴的两个端点
轴上,以两个焦点和短轴的两个端点
为顶点的四边形是一个面积为8的正方形(记为Q).
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点P是椭圆C的左准线与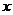 轴的交点,过点P的直线
轴的交点,过点P的直线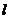 与椭圆C相交于M,N两点,当线段MN的中点落在正方形Q内(包括边界)时,求直线
与椭圆C相交于M,N两点,当线段MN的中点落在正方形Q内(包括边界)时,求直线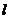 的斜率的取值范围。
的斜率的取值范围。
解:
(Ⅰ)依题意,设椭圆C的方程为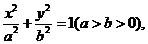 焦距为
焦距为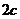 ,
,
由题设条件知,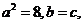 所以
所以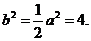
故椭圆C的方程为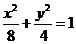 .
.
(Ⅱ)椭圆C的左准线方程为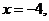 所以点P的坐标
所以点P的坐标 ,
,
显然直线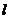 的斜率
的斜率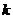 存在,所以直线
存在,所以直线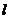 的方程为
的方程为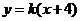 。
。 

如图,设点M,N的坐标分别为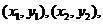 线段MN的中点为G
线段MN的中点为G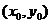 ,
,
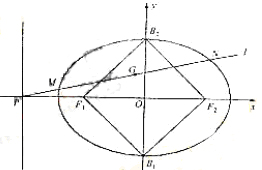
由 得
得 . ……①
. ……①
由 解得
解得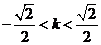 .
……②
.
……②
因为 是方程①的两根,所以
是方程①的两根,所以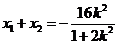 ,于是
,于是
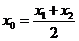 =
= ,
,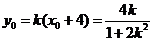 .
.
因为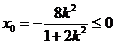 ,所以点G不可能在
,所以点G不可能在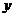 轴的右边,
轴的右边,
又直线 ,
,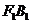 方程分别为
方程分别为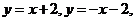
所以点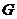 在正方形
在正方形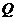 内(包括边界)的充要条件为
内(包括边界)的充要条件为
 即
即 亦即
亦即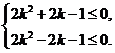


解得 ,此时②也成立.
,此时②也成立.
故直线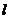 斜率的取值范围是
斜率的取值范围是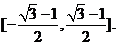
19.(本小题满分13分)
已知函数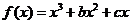 的导函数的图象关于直线x=2对称.
的导函数的图象关于直线x=2对称.
(Ⅰ)求b的值;
(Ⅱ)若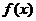 在
在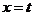 处取得最小值,记此极小值为
处取得最小值,记此极小值为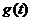 ,求
,求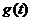 的定义域和值域。
的定义域和值域。
解: (Ⅰ)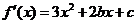 .因为函数
.因为函数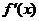 的图象关于直线x=2对称,
的图象关于直线x=2对称,
所以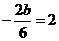 ,于是
,于是
(Ⅱ)由(Ⅰ)知, ,
,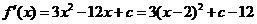 .
.
(ⅰ)当c 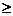 12时,
12时,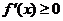 ,此时
,此时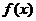 无极值。
无极值。
(ii)当c<12时,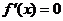 有两个互异实根
有两个互异实根 ,
,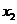 .不妨设
.不妨设 <
<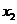 ,则
,则 <2<
<2<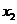 .
.
当x< 时,
时,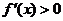 ,
, 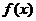 在区间
在区间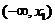 内为增函数;
内为增函数;
当 <x<
<x<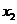 时,
时, ,
,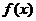 在区间
在区间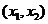 内为减函数;
内为减函数;
当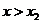 时,
时,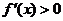 ,
,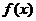 在区间
在区间 内为增函数.
内为增函数.
所以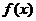 在
在 处取极大值,在
处取极大值,在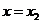 处取极小值.
处取极小值.
因此,当且仅当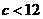 时,函数
时,函数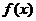 在
在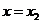 处存在唯一极小值,所以
处存在唯一极小值,所以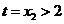 .
.
于是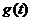 的定义域为
的定义域为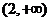 .由
.由 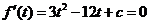 得
得 .
.
于是 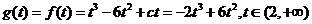 .
.
当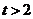 时,
时,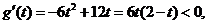 所以函数
所以函数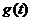
在区间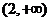 内是减函数,故
内是减函数,故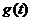 的值域为
的值域为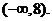


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com