
1、[2009年高考题上海卷第22小题]如图(a),质量m=1kg的物体沿倾角q=37°的固定粗糙斜面由静止开始向下运动,风对物体的作用力沿水平方向向右,其大小与风速v成正比,比例系数用k表示,物体加速度a与风速v的关系如图(b)所示。求:
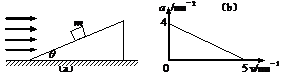
(1)物体与斜面间的动摩擦因数m;(2)比例系数k。
(sin370=0.6,cos370=0.8,g=10m/s2)
23.(09年广东卷B) 罗斯福担任总统之前,美国出版的一本书提议政府增加开支,甚至不惜造成财政赤字,以便舒缓经济衰退。罗斯福读后批注:“哪有此等好事--天下没有不劳而获的东西。”这表明
 (
)
(
)
A.罗斯福始终是信奉新政理念的政治家

B.罗斯福上台之前美国尚未出现经济衰退

C.罗斯福新政的理念在罗斯福担任总统前已经萌生

D.罗斯福在没有率先提出了政府干预经济的主张 

[答案]C
[解析] 本题的关键是理解材料中在罗斯福就任总统之前读的那本书的提议实质就是后来罗斯福新政的理念--国家干预经济。所以选C。而当时罗斯福的批注又说明罗斯福当时并不赞成这种理念。所以排除A选项和D选项,B选项与材料和史实都是不符合的。
[考点定位]本题考查的是对罗斯福新政的理解。
18.(09年江苏卷)罗斯福新政时期,美国政府大力兴办公共工程,其客观作用包括( )
①扩大生产资料市场 ②增加就业机会
③刺激消费需求 ④抑制物价上涨
A.②③ B.①②③ C.①②④ D.①③④
[答案]B
23.(09年重庆卷)美国前总统乔治·布什在出席博鳌亚洲论坛2009年年会时表示,世界各国要紧密合作应对金融危机,保护主义无助于克服困难然而,在1929-1933年世界经济危机期间,正是美国带头大幅度提高关税,从而引发了一场关税大战。其直接影响是( )
A.资本主义各国间的矛盾日趋尖锐 B.资本主义各国政坛丑闻频出
C.资本主义各国社会危机日益加深 D.资本主义各国政府信誉扫地
[答案]A
22.(本小题满分12分)
已知双曲线C的方程为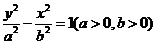 ,离心率
,离心率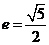 ,顶点到渐近线的距离为
,顶点到渐近线的距离为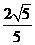 。
。
(I) 求双曲线C的方程;
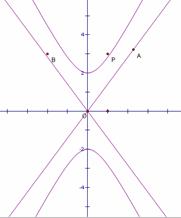 (II)如图,P是双曲线C上一点,A,B两点在双曲线C的两条渐近线上,且分别位于第一、二象限,若
(II)如图,P是双曲线C上一点,A,B两点在双曲线C的两条渐近线上,且分别位于第一、二象限,若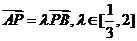 ,求
,求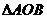 面积的取值范围。
面积的取值范围。
解析:
解法1(Ⅰ)由题意知,双曲线C的顶点(0,a)到渐近线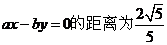 ,
,
所以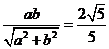 所以
所以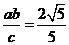
由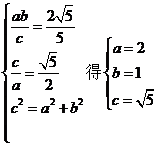
所以曲线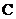 的方程是
的方程是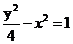
(Ⅱ)由(Ⅰ)知双曲线C的两条渐近线方程为
设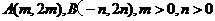
由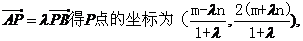
将P点的坐标代入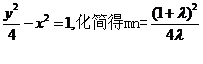
因为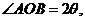
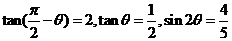
又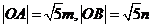
所以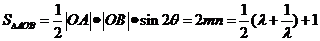
记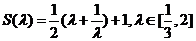
则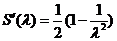
由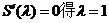
又S(1)=2,
当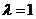 时,
时,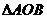 面积取到最小值
面积取到最小值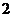 ,当当
,当当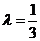 时,
时,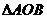 面积取到最大值
面积取到最大值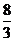
所以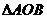 面积范围是
面积范围是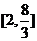
解答2(Ⅰ)由题意知,双曲线C的顶点(0,a)到渐近线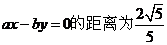 ,
,
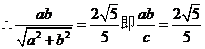
由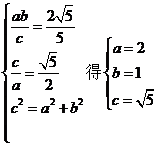
所以曲线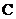 的方程是
的方程是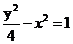 .
.
(Ⅱ)设直线AB的方程为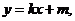
由题意知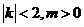
由
由
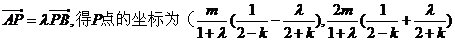
将P点的坐标代入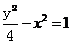 得
得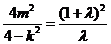
设Q为直线AB与y轴的交点,则Q点的坐标为(0,m)
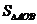 =
=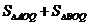
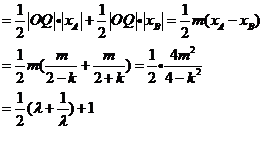
以下同解答1
21.(本小题满分12分)
已知数列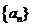 满足,
满足, 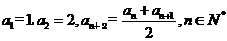 .
.
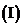 令
令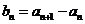 ,证明:
,证明: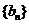 是等比数列;
是等比数列;
(Ⅱ)求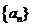 的通项公式。
的通项公式。
(1)证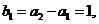
当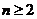 时,
时,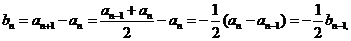
所以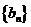 是以1为首项,
是以1为首项,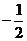 为公比的等比数列。
为公比的等比数列。
(2)解由(1)知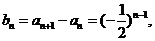
当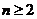 时,
时,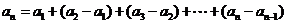
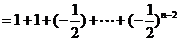
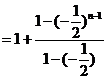

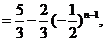
当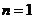 时,
时,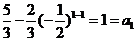 。
。
所以 。
。
20.(本小题满分12分)
已知函数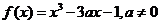
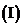 求
求 的单调区间;
的单调区间;
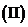 若
若 在
在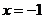 处取得极值,直线y=my与
处取得极值,直线y=my与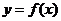 的图象有三个不同的交点,求m的取值范围。
的图象有三个不同的交点,求m的取值范围。
解析:(1)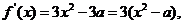
当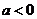 时,对
时,对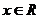 ,有
,有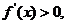
当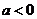 时,
时, 的单调增区间为
的单调增区间为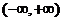
当 时,由
时,由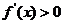 解得
解得 或
或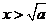 ;
;
由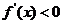 解得
解得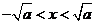 ,
,
当 时,
时, 的单调增区间为
的单调增区间为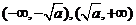 ;
; 的单调减区间为
的单调减区间为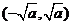 。
。
(2)因为 在
在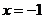 处取得极大值,
处取得极大值,
所以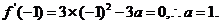
所以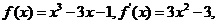
由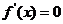 解得
解得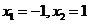 。
。
由(1)中 的单调性可知,
的单调性可知, 在
在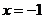 处取得极大值
处取得极大值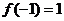 ,
,
在 处取得极小值
处取得极小值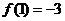 。
。
因为直线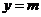 与函数
与函数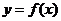 的图象有三个不同的交点,又
的图象有三个不同的交点,又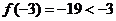 ,
,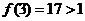 ,
,
结合 的单调性可知,
的单调性可知,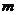 的取值范围是
的取值范围是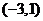 。
。
所以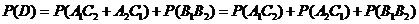
由事件的独立性的
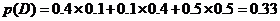
解答2(Ⅰ)设事件A表示“一个月内被投诉2次”设事件B表示“一个月内被投诉的次数不超过1次”
所以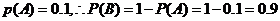
(Ⅱ)同解答1(Ⅱ)
19.(本小题满分12分)
如图,直三棱柱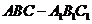 中, AB=1,
中, AB=1,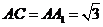 ,∠ABC=60
,∠ABC=60 .
.

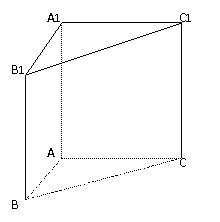 (Ⅰ)证明:
(Ⅰ)证明: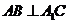 ;
;
(Ⅱ)求二面角A-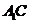 -B的大小。
-B的大小。
解析:解答1(Ⅰ)
因为三棱柱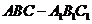 为直三棱柱所以
为直三棱柱所以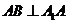
在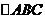 中
中
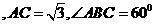
由正弦定理得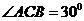 所以
所以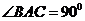
即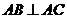 ,所以
,所以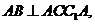 又因为
又因为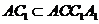 所以
所以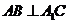
(Ⅱ)如图所示,作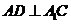 交
交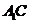 于
于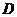 ,连
,连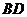 ,由三垂线定理可得
,由三垂线定理可得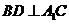
所以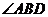 为所求角,在
为所求角,在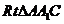 中,
中,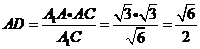 ,在
,在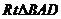 中,
中,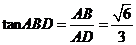 ,所以
,所以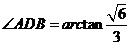

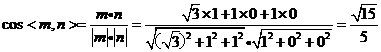
所以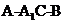 所成角是
所成角是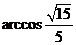
18.(本小题满分12分)
椐统计,某食品企业一个月内被消费者投诉的次数为0,1,2的概率分别为0.4,0.5,0.1
(Ⅰ) 求该企业在一个月内共被消费者投诉不超过1次的概率;
(Ⅱ)假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率。
解析:解答1(Ⅰ)设事件A表示“一个月内被投诉的次数为0”事件B表示“一个月内被投诉的次数为1”
所以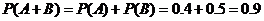
(Ⅱ)设事件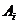 表示“第
表示“第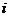 个月被投诉的次数为0”事件
个月被投诉的次数为0”事件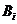 表示“第
表示“第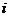 个月被投诉的次数为1”事件
个月被投诉的次数为1”事件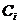 表示“第
表示“第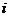 个月被投诉的次数为2”事件D表示“两个月内被投诉2次”
个月被投诉的次数为2”事件D表示“两个月内被投诉2次”
所以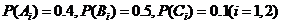
所以两个月中,一个月被投诉2次,另一个月被投诉0次的概率为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com