

3.会求函数在某点的导数.
教学重点:
瞬时速度、瞬时变化率的概念、导数的概念.
教学难点:
导数的概念.
教学过程:
2.理解导数的概念,知道瞬时变化率就是导数,体会导数的思想及其内涵;
§1.1.2 导数的概念
教学目标:
1.了解瞬时速度、瞬时变化率的概念;
2.函数在某点处附近的平均变化率.
1.平均变化率的概念.
3.过曲线 上两点
上两点 和
和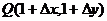 作曲线的割线,
作曲线的割线,
求出当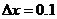 时割线的斜率.
时割线的斜率.
2.物体按照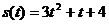 的规律作直线运动,求在
的规律作直线运动,求在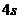 附近的平均变化率.
附近的平均变化率.
1.质点运动规律为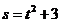 ,则在时间
,则在时间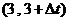 中相应的平均速度为
.
中相应的平均速度为
.
例1 已知函数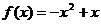 的图象上的一点
的图象上的一点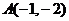 及
及
临近一点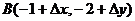 则
则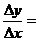 .
.
解: 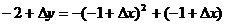
∴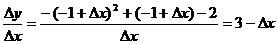
例2 求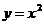 在
在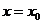 附近的平均变化率.
附近的平均变化率.
解: 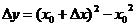
所以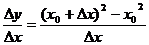
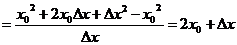
所以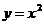 在
在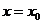 附近的平均变化率为
附近的平均变化率为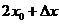
(二)平均变化率概念
1.上述问题中的变化率可用式子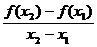 表示,
表示,
称为函数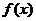 从
从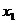 到
到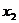 的平均变化率.
的平均变化率.
2. 若设
若设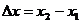 ,
, 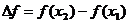 (这里
(这里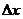 看作是对于
看作是对于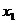 的一个“增量”可用
的一个“增量”可用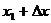 代替
代替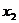 ,同样
,同样 )
)
则平均变化率为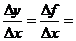
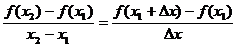
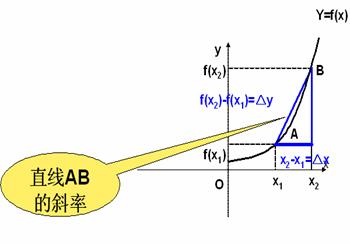
思考: 观察函数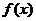 的图象
的图象
平均变化率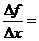
 表示什么?
表示什么?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com