
10.甲乙两名篮球队员独立地轮流投篮,直到某人投中为止。甲投中的概率为0.4,乙为0.6,分别求出甲乙两人投篮次数的分布列。(假设甲先投)
解:设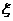 为甲投篮的次数,
为甲投篮的次数,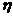 为乙投篮的次数,
为乙投篮的次数,
(1)设事件A=前k-1次均不中,第k次甲中;B=前k-1次均不中,第k次甲不中而乙投中,则A与B互斥,故有: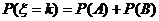
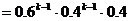
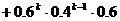
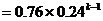 (
(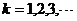 )
)
(2)设事件B=前k-1次均不中,第k次甲不中而乙投中,C=前k次均不中,第k+1次甲投中,则B与C互斥,故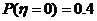 ,
, 
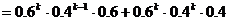
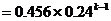 (
(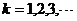 )
)
[探索题]A、B两个代表队进行乒乓球对抗赛,每队三名队员,A队队员是A1、A2、A3,B队队员是B1、B2、B3,按以往多次比赛的统计,对阵队员之间胜负概率如下:
|
对阵队员 |
A队员胜的概率 |
A队员负的概率 |
|
A1对B1 |
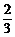 |
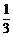 |
|
A2对B2 |
 |
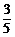 |
|
A3对B3 |
 |
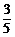 |
现按表中对阵方式出场,每场胜队得1分,负队得0分.设A队、B队最后所得总分分别为ξ、η
(1)求ξ、η的概率分布;
(2)求Eξ、Eη
解:(1)ξ、η的可能取值分别为3,2,1,0
P(ξ=3)=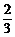 ×
× ×
× =
= ,
,
P(ξ=2)=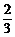 ×
× ×
×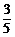 +
+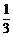 ×
× ×
× +
+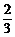 ×
×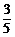 ×
× =
=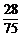 ,
,
P(ξ=1)=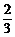 ×
×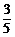 ×
×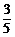 +
+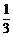 ×
× ×
×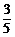 +
+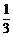 ×
×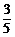 ×
× =
= ,
,
P(ξ=0)=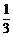 ×
×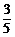 ×
×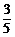 =
=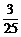 ;
;
根据题意知ξ+η=3,所以
P(η=0)=P(ξ=3)= ,P(η=1)=P(ξ=2)=
,P(η=1)=P(ξ=2)=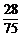 ,
,
P(η=2)=P(ξ=1)= ,P(η=3)=P(ξ=0)=
,P(η=3)=P(ξ=0)=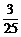
(2)Eξ=3× +2×
+2×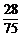 +1×
+1× +0×
+0×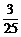 =
=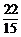 ;
;
因为ξ+η=3,所以Eη=3-Eξ=
9.金工车间有10台同类型的机床,每台机床配备的电动机功率为10 kW,已知每台机床工作时,平均每小时实际开动12 min,且开动与否是相互独立的 现因当地电力供应紧张,供电部门只提供50 kW的电力,这10台机床能够正常工作的概率为多大?在一个工作班的8 h内,不能正常工作的时间大约是多少?
现因当地电力供应紧张,供电部门只提供50 kW的电力,这10台机床能够正常工作的概率为多大?在一个工作班的8 h内,不能正常工作的时间大约是多少?
解:设10台机床中实际开动的机床数为随机变量ξ,由于机床类型相同,且机床的开动与否相互独立,因此ξ-B(10,p) 其中p是每台机床开动的概率,由题意p=
其中p是每台机床开动的概率,由题意p=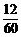 =
=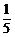 从而P(ξ=k)=C
从而P(ξ=k)=C (
(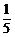 )k(
)k(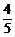 )10-k,k=0,1,2,…,10
)10-k,k=0,1,2,…,10
50 kW电力同时供给5台机床开动,因而10台机床同时开动的台数不超过5台时都可以正常工作,这一事件的概率为P(ξ≤5),
P(ξ≤5)=C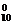 (
(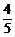 )10+C
)10+C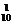 ·
·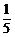 ·(
·(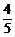 )9+C
)9+C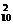 (
(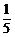 )2·(
)2·(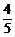 )8+C
)8+C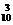 (
(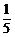 )3(
)3(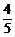 )7+C
)7+C (
(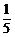 )4·(
)4·(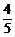 )6+C
)6+C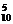 (
(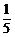 )5·(
)5·(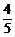 )5≈0.994
)5≈0.994
因此,在电力供应为50 kW的条件下,机床不能正常工作的概率仅约为0 006,从而在一个工作班的8 h内,不能正常工作的时间只有大约8×60×0
006,从而在一个工作班的8 h内,不能正常工作的时间只有大约8×60×0 006=2
006=2 88(min),这说明,10台机床的工作基本上不受电力供应紧张的影响
88(min),这说明,10台机床的工作基本上不受电力供应紧张的影响
8. 在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券中任抽2张,求:(Ⅰ)该顾客中奖的概率;
(Ⅱ)该顾客获得的奖品总价值ξ(元)的概率分布列.
思路分析:随机取出2张奖券奖品总价值的可能情况有:0,10,20,50,60,求出ξ取每一个值时的概率,列出分布列,根据离散型随机变量的期望与方差的概念、公式及性质解答.
解:(Ⅰ) ,即该顾客中奖的概率为
,即该顾客中奖的概率为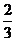 .
.
(Ⅱ)ξ的所有可能值为:0,10,20,50,60(元).
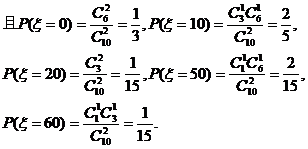
故ξ有分布列:
|
ξ |
0 |
10 |
20 |
50 |
60 |
|
P |
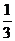 |
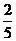 |
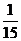 |
 |
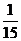 |
7.(2006广东) 某运动员射击一次所得环数x的分布列如下:
|
x |
0-6 |
7 |
8 |
9 |
10 |
|
p |
0 |
0. 2 |
0. 3 |
0. 3 |
0. 2 |
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为ξ
(Ⅰ)求该运动员两次都命中7环的概率;
(Ⅱ)求ξ分布列;
(Ⅲ) 求ξ的数学希望
解:(Ⅰ)求该运动员两次都命中7环的概率为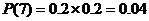 ;
;
(Ⅱ) ξ的可能取值为7, 8 ,9 , 10
ξ的可能取值为7, 8 ,9 , 10
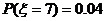
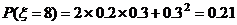
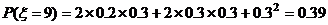
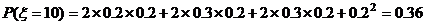
ξ分布列为
|
ξ |
7 |
8 |
9 |
10 |
|
P |
0 04 04 |
0 21 21 |
0 39 39 |
0 36 36 |
(Ⅲ) 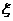 的数学希望为
的数学希望为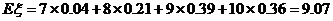
6.随机变量ξ的可能取值为1,2,3。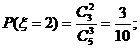
[解答题]
5. P(ξ≤6)=P(ξ=4)+P(ξ=6)=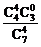 +
+ =
=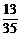 .
.
6.一袋中装有5只球,编号为1,2,3,4,5,在袋中同时取3只,以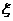 表示取出的三只球中的最小号码,则随机变量ξ的取值为__________,ξ=2的概率为_________.
表示取出的三只球中的最小号码,则随机变量ξ的取值为__________,ξ=2的概率为_________.
◆练习简答:1-3.BBC; 4.P(ξ=k)=C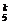 0.3k0.75-k,k=0,1,…,5
0.3k0.75-k,k=0,1,…,5
5.袋中有4只红球3只黑球,从袋中任取4只球,取到1只红球得1分,取到1只黑球得3分,设得分为随机变量ξ,则P(ξ≤6)=________.
4.现有一大批种子,其中优质良种占30%,从中任取5粒,记ξ为5粒中的优质良种粒数,则ξ的分布列是________.
3.在15个村庄中,有7个村庄交通不方便,现从中任选10个村庄,用ξ表示这10个村庄中交通不方便的村庄数,下列概率中等于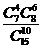 的是 ( )
的是 ( )
A.P(ξ=2) B.P(ξ≤2) C.P(ξ=4) D.P(ξ≤4)
[填空题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com