
3.  是等差数列
是等差数列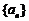 的前n项和,
的前n项和,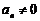 ,若
,若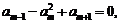
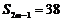 ,则m = 。
,则m = 。
2. 等差数列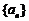 中,
中,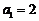 ,公差不为零,且
,公差不为零,且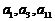 恰为某等比数列的前3项,那么该等比数列的公比等于 。
恰为某等比数列的前3项,那么该等比数列的公比等于 。
1. 数列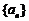 中,
中,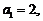
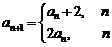
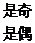 ,则
,则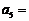 。
。
5. 数列与函数等相联系的综合问题。
4. 与数列知识相关的应用题;
3. 等差、等比数列的重要性质;
2. 等差、等比数列的通项、前n项和公式;
1. 数列的概念,等差、等比数列的基本概念;
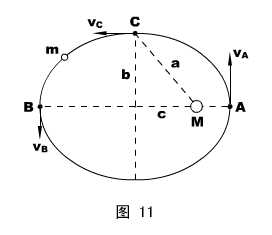 物理情形:地球和太阳的质量分别为m和M ,地球绕太阳作椭圆运动,轨道的半长轴为a ,半短轴为b ,如图11所示。试求地球在椭圆顶点A、B、C三点的运动速度,以及轨迹在A、C两点的曲率半径。
物理情形:地球和太阳的质量分别为m和M ,地球绕太阳作椭圆运动,轨道的半长轴为a ,半短轴为b ,如图11所示。试求地球在椭圆顶点A、B、C三点的运动速度,以及轨迹在A、C两点的曲率半径。
模型分析:求解天体运动的本来模式,常常要用到开普勒定律(定量)、机械能守恒(万有引力势能)、椭圆的数学常识等等,相对高考要求有很大的不同。
地球轨道的离心率很小(其值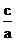 ≈0.0167 ,其中c为半焦距),这是我们常常能将它近似为圆的原因。为了方便说明问题,在图11中,我们将离心率夸大了。
≈0.0167 ,其中c为半焦距),这是我们常常能将它近似为圆的原因。为了方便说明问题,在图11中,我们将离心率夸大了。
针对地球从A点运动到B点的过程,机械能守恒
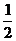 m
m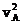 +(-
+(-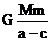 )=
)= 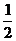 m
m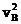 +(-
+(-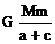 )
)
比较A、B两点,应用开普勒第二定律,有:vA(a-c)= vB(a + c)
结合椭圆的基本关系:c = 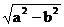
解以上三式可得:vA = 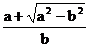
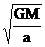 , vB
=
, vB
= 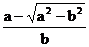
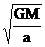
再针对地球从A到C的过程,应用机械能守恒定律,有
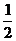 m
m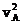 +(-
+(-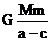 )=
)= 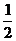 m
m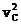 +(-
+(-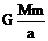 )
)
代入vA值可解得:vC = 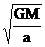
为求A、C两点的曲率半径,在A、C两点建自然坐标,然后应用动力学(法向)方程。
在A点,F万 = ΣFn = m an ,设轨迹在A点的曲率半径为ρA ,即:G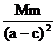 = m
= m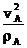
 代入vA值可解得:ρA =
代入vA值可解得:ρA = 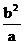
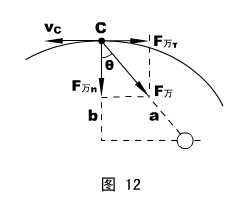
在C点,方程复杂一些,须将万有引力在τ、n方向分解,如图12所示。
然后,F万n =ΣFn = m an ,即:F万cosθ= m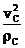
即:G ·
·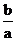 = m
= m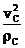
代入vC值可解得:ρC = 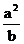
值得注意的是,如果针对A、C两点用开普勒第二定律,由于C点处的矢径r和瞬时速度vC不垂直,方程不能写作vA(a-c)= vC a 。
正确的做法是:将vC分解出垂直于矢径的分量(分解方式可参看图12,但分解的平行四边形未画出)vC cosθ,再用vA(a-c)=(vC cosθ)a ,化简之后的形式成为
vA(a-c)= vC b
要理解这个关系,有一定的难度,所以建议最好不要对A、C两点用开普勒第二定律
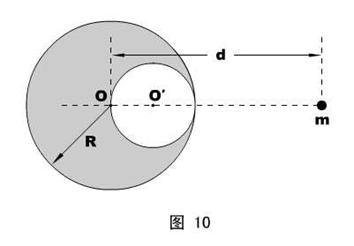 物理情形:如图9所示,半径为R的均质球质量为M,球心在O点,现在被内切的挖去了一个半径为R/2的球形空腔(球心在O′)。在O、O′的连线上距离O点为d的地方放有一个很小的、质量为m的物体,试求这两个物体之间的万有引力。
物理情形:如图9所示,半径为R的均质球质量为M,球心在O点,现在被内切的挖去了一个半径为R/2的球形空腔(球心在O′)。在O、O′的连线上距离O点为d的地方放有一个很小的、质量为m的物体,试求这两个物体之间的万有引力。
模型分析:无论是“基本条件”还是“拓展条件”,本模型都很难直接符合,因此必须使用一些特殊的处理方法。本模型除了照应万有引力的拓展条件之外,着重介绍“填补法”的应用。
空腔里现在虽然空无一物,但可以看成是两个半径为R/2的球的叠加:一个的质量为+M/8 ,一个的质量为-M/8 。然后,前者正好填补空腔--和被挖除后剩下的部分构成一个完整的均质球A ;注意后者,虽然是一个比较特殊的物体(质量为负值),但仍然是一个均质的球体,命名为B 。
既然A、B两物均为均质球体,他们各自和右边小物体之间的万有引力,就可以使用“拓展条件”中的定势来计算了。只是有一点需要说明,B物的质量既然负值,它和m之间的万有“引力”在方向上不再表现为吸引,而应为排斥--成了“万有斥力”了。具体过程如下
FAm = G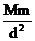
FBm = G = -G
= -G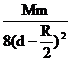
最后,两物之间的万有引力 F = FAm
+ FBm = G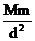 -G
-G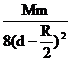
需要指出的是,在一部分同学的心目中,可能还会存在另一种解题思路,那就是先通过力矩平衡求被挖除物体的重心(仍然要用到“填补法”、负质量物体的重力反向等),它将在O、O′的连线上距离O点左侧R/14处,然后“一步到位”地求被挖除物与m的万有引力
F = G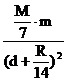
然而,这种求法违背了万有引力定律适用的条件,是一种错误的思路。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com