
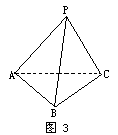
3.在四面体P-ABC中,∠APB=∠BPC=∠CPA=90°,各棱长的和为m,求这个四面体体积的最大值.
2. 证明:通过水管放水,当流速相同时,如果水管截面的周长相等,那么截面是圆的水管比截面是正方形的水管流量大.
证明:通过水管放水,当流速相同时,如果水管截面的周长相等,那么截面是圆的水管比截面是正方形的水管流量大.
1.某工厂要建造一个长方体无盖贮水池,其容积为4800m3,深为3m,如果池底每1m2的造价为150元,池壁每1m2的造价为120元,问怎样设计水池能使总造价最低,最低总造价是多少元?
2.函数模型除了常见的“正比例函数、反比例函数、一次函数、二次函数、幂函数、指数函数、对数函数、三角函数、反三角函数”等标准形式外,又出现了以“函数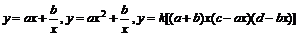 ”
”
为模型的新的形式.
三 经典例题导讲
[例1]求y=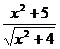 的最小值.
的最小值.
错解: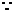 y=
y=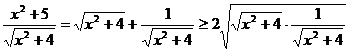 =2
=2
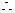 y的最小值为2.
y的最小值为2.
错因:等号取不到,利用均值定理求最值时“正、定、等”这三个条件缺一不可.
正解:令t=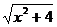 ,则t
,则t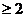 ,于是y=
,于是y=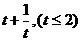
由于当t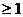 时,y=
时,y=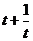 是递增的,故当t=2即x=0时,y取最小值
是递增的,故当t=2即x=0时,y取最小值 .
.
[例2]m为何值时,方程x2+(2m+1)x+m2-3=0有两个正根.
错解:由根与系数的关系得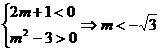 ,因此当
,因此当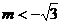 时,原方程有两个正根.
时,原方程有两个正根.
错因:忽视了一元二次方程有实根的条件,即判别式大于等于0.
正解:由题意: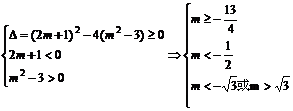
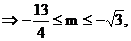 因此当
因此当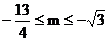 时,原方程有两个正根.
时,原方程有两个正根.
[例3]若正数x,y满足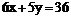 ,求xy的最大值.
,求xy的最大值.
解:由于x,y为正数,则6x,5y也是正数,所以
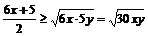
当且仅当6x=5y时,取“=”号.
因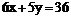 ,则
,则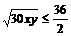 ,即
,即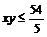 ,所以
,所以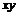 的最大值为
的最大值为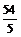 .
.
[例4] 已知:长方体的全面积为定值S,试问这个长方体的长、宽、高各是多少时,它的体积最大,求出这个最大值.
分析:经过审题可以看出,长方体的全面积S是定值.因此最大值一定要用S来表示.首要问题是列出函数关系式.设长方体体积为y,其长、宽、高分别为a,b,c,则y=abc.由于a+b+c不是定值,所以肯定要对函数式进行变形.可以利用平均值定理先求出y2的最大值,这样y的最大值也就可以求出来了.
解:设长方体的体积为y,长、宽、高分别是为a,b,c,则
y=abc,2ab+2bc+2ac=S.
而
y2=(abc)2=(ab)(bc)(ac)
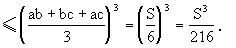
当且仅当ab=bc=ac,即a=b=c时,上式取“=”号,y2有最小值
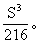
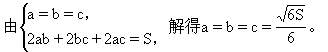
答:长方体的长、宽、高都等于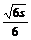 时体积的最大值为
时体积的最大值为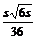 .
.
说明:对应用问题的处理,要把实际问题转化成数学问题,列好函数关系式是求解问题的关健.
不等式既属数学的基础知识,又是解决数学问题的重要工具,在解决函数定义域、值域、单调性、恒成立问题、方程根的分布、参数范围的确定、曲线位置关系的讨论、解析几何、立体几何中的最值等问题中有广泛的应用,特别是近几年来,高考试题带动了一大批实际应用题问世,其特点是:
1.问题的背景是人们关心的社会热点问题,如“物价、税收、销售收入、市场信息”等,题目往往篇幅较长.
3.涉及不等式知识解决的实际应用问题,这些问题大体分为两类:一是建立不等式解不等式;二是建立函数式求最大值或最小值.
2.求函数定义域、值域、方程的有解性、判断函数单调性及单调区间,确定参数的取值范围等.这些问题一般转化为解不等式或不等式组,或证明不等式.
1.利用均值不等式求最值:如果a1,a2∈R+,那么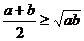 .
.
6.证明:若a > 0,则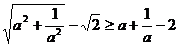
§5.4不等式的应用
5.若x > 1,y > 1,求证: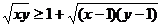
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com