
2.已知直线x=a(a>0)和圆(x-1)2+y2=4相切 ,那么a的值是( )
A.5 B.4 C.3 D.2
1.直线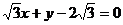 截圆
截圆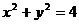 得的劣弧所对的圆心角为 (
)
得的劣弧所对的圆心角为 (
)
A. B. C. D.
[例1]直线l经过P(2,3),且在x,y轴上的截距相等,试求该直线方程.
错解:设直线方程为: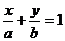 ,又过P(2,3),∴
,又过P(2,3),∴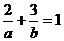 ,求得a=5
,求得a=5
∴直线方程为x+y-5=0.
错因:直线方程的截距式: 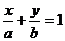 的条件是:
的条件是: ≠0且b≠0,本题忽略了
≠0且b≠0,本题忽略了 这一情形.
这一情形.
正解:在原解的基础上,再补充这样的过程:当直线过(0,0)时,此时斜率为: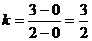 ,
,
∴直线方程为y=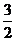 x
x
综上可得:所求直线方程为x+y-5=0或y=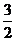 x
.
x
.
[例2]已知动点P到y轴的距离的3倍等于它到点A(1,3)的距离的平方,求动点P的轨迹方程.
错解:设动点P坐标为(x,y).由已知3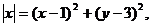
化简3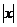 =x2-2x+1+y2-6y+9
.
=x2-2x+1+y2-6y+9
.
当x≥0时得x2-5x+y2-6y+10=0 . ①
当x<0时得x2+ x+y2-6y+10=0 . ②
错因:上述过程清楚点到y轴距离的意义及两点间距离公式,并且正确应用绝对值定义将方程分类化简,但进一步研究化简后的两个方程,配方后得
(x-)2+(y-3)2 = ① 和 (x+)2+(y-3)2 = - ②
两个平方数之和不可能为负数,故方程②的情况不会出现.
正解: 接前面的过程,∵方程①化为(x-)2+(y-3)2 = ,方程②化为(x+)2+(y-3)2 = - ,由于两个平方数之和不可能为负数,故所求动点P的轨迹方程为: (x-)2+(y-3)2 = (x≥0)
[例3]m是什么数时,关于x,y的方程(2m2+m-1)x2+(m2-m+2)y2+m+2=0的图象表示一个圆?
错解:欲使方程Ax2+Cy2+F=0表示一个圆,只要A=C≠0,
得2m2+m-1=m2-m+2,即m2+2m-3=0,解得m1=1,m2=-3,
∴当m=1或m=-3时,x2和y2项的系数相等,这时,原方程的图象表示一个圆
错因:A=C,是Ax2+Cy2+F=0表示圆的必要条件,而非充要条件,其充要条件是:
A=C≠0且<0.
正解:欲使方程Ax2+Cy2+F=0表示一个圆,只要A=C≠0,
得2m2+m-1=m2-m+2,即m2+2m-3=0,解得m1=1,m2=-3,
(1) 当m=1时,方程为2x2+2y2=-3不合题意,舍去.
(2) 当m=-3时,方程为14x2+14y2=1,即x2+y2=,原方程的图形表示圆.
[例4]自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在的直线方程.
错解:设反射光线为L′,由于L和L′关于x轴对称,L过点A(-3,3),点A关于x轴的对称点A′(-3,-3),于是L′过A(-3,-3).
设L′的斜率为k,则L′的方程为y-(-3)=k[x-(-3)],即kx-y+3k-3=0,
已知圆方程即(x-2)2+(y-2)2=1,圆心O的坐标为(2,2),半径r=1
因L′和已知圆相切,则O到L′的距离等于半径r=1
即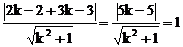
整理得12k2-25k+12=0
解得k=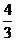 L′的方程为y+3=
L′的方程为y+3=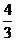 (x+3)
(x+3)
即4x-3y+3=0 因L和L′关于x轴对称
故L的方程为4x+3y+3=0.
错因:漏解
正解:设反射光线为L′,由于L和L′关于x轴对称,L过点A(-3,3),点A关于x轴的对称点A′(-3,-3), 于是L′过A(-3,-3).
设L′的斜率为k,则L′的方程为y-(-3)=k[x-(-3)],即kx-y+3k-3=0,
已知圆方程即(x-2)2+(y-2)2=1,圆心O的坐标为(2,2),半径r=1
因L′和已知圆相切,则O到L′的距离等于半径r=1
即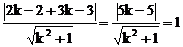
整理得12k2-25k+12=0
解得k=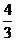 或k=
或k=
L′的方程为y+3=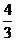 (x+3);或y+3=
(x+3);或y+3= (x+3)。
(x+3)。
即4x-3y+3=0或3x-4y-3=0
因L和L′关于x轴对称
故L的方程为4x+3y+3=0或3x+4y-3=0.
[例5]求过直线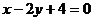 和圆
和圆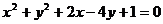 的交点,且满足下列条件之一的圆的方程:
的交点,且满足下列条件之一的圆的方程:
(1) 过原点;(2)有最小面积.
解:设所求圆的方程是: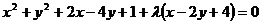
即: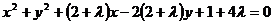
(1)因为圆过原点,所以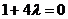 ,即
,即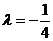
故所求圆的方程为: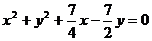 .
.
(2) 将圆系方程化为标准式,有:
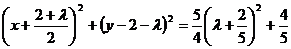
当其半径最小时,圆的面积最小,此时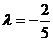 为所求.
为所求.
故满足条件的圆的方程是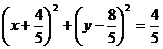 .
.
点评:(1)直线和圆相交问题,这里应用了曲线系方程,这种解法比较方便;当然也可以待定系数法。(2)面积最小时即圆半径最小。也可用几何意义,即直线与相交弦为直径时圆面积最小.
[例6](06年辽宁理科)已知点A(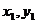 ),B(
),B(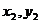 )(
)(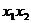 ≠0)是抛物线
≠0)是抛物线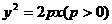 上的两个动点,O是坐标原点,向量
上的两个动点,O是坐标原点,向量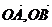 满足|
满足|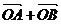 |=|
|=|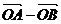 |.设圆C的方程为
|.设圆C的方程为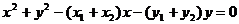
(1)证明线段AB是圆C的直径;
(2)当圆C的圆心到直线 的距离的最小值为
的距离的最小值为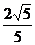 时,求
时,求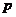 的值.
的值.
解:(1)证明 ∵|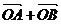 |=|
|=|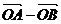 |,∴(
|,∴(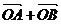 )2=(
)2=(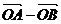 )2,
)2,
整理得: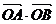 =0 ∴
=0 ∴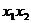 +
+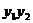 =0
=0
设M(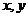 )是以线段AB为直径的圆上的任意一点,则
)是以线段AB为直径的圆上的任意一点,则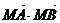 =0
=0
即 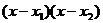 +
+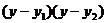 =0
=0
整理得: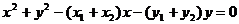
故线段AB是圆C的直径.
(2)设圆C的圆心为C(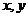 ),则
),则
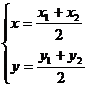
∵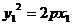 ,
,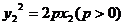
∴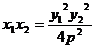
又∵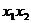 +
+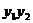 =0 ,
=0 ,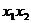 =-
=-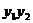
∴-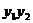
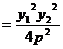
∵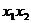 ≠0,∴
≠0,∴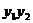 ≠0
≠0
∴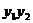 =-4
=-4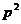
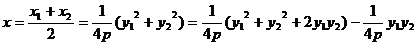
=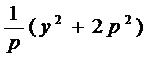
所以圆心的轨迹方程为
设圆心C到直线 的距离为d,则
的距离为d,则
=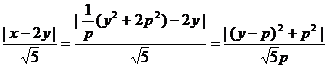
当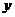 =
=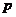 时,d有最小值
时,d有最小值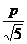 ,由题设得
,由题设得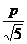 =
=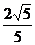
∴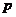 =2.
=2.
2.两圆的位置关系的判定方法.
设两圆圆心分别为O1、O2,半径分别为 1,
1, 2,|O1O2|为圆心距,则两圆位置关系如下:
2,|O1O2|为圆心距,则两圆位置关系如下:
|O1O2|> 1+
1+ 2
2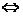 两圆外离;
两圆外离;
|O1O2|= 1+
1+ 2
2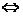 两圆外切;
两圆外切;
|  1-
1- 2|<|O1O2|<
2|<|O1O2|< 1+
1+ 2
2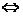 两圆相交;
两圆相交;
| O1O2 |=| 1-
1- 2|
2|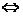 两圆内切;
两圆内切;
0<| O1O2|<|  1-
1- 2|
2| 两圆内含.
两圆内含.
1.直线与圆的位置关系的判定方法.
(1)方法一 直线: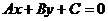 ;圆:
;圆: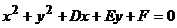 .
.
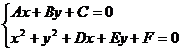
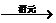 一元二次方程
一元二次方程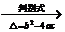
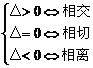
(2)方法二 直线: 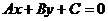 ;圆:
;圆: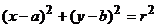 ,圆心(
,圆心( ,b)到直线的距离为
,b)到直线的距离为
d=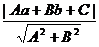

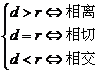
8.确定圆方程需要有三个互相独立的条件。圆的方程有两种形式,要知道两种形式之间的相互转化及相互联系
(1)圆的标准方程: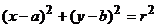 ,其中(
,其中( ,b)是圆心坐标,
,b)是圆心坐标, 是圆的半径;
是圆的半径;
(2)圆的一般方程: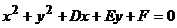 (
(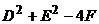 >0),圆心坐标为(-
>0),圆心坐标为(-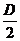 ,-
,-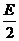 ),半径为
),半径为 =
=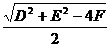 .
.
7.点到直线的距离公式.
(1)已知一点P(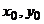 )及一条直线
)及一条直线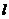 :
: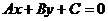 ,则点P到直线
,则点P到直线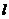 的距离d=
的距离d=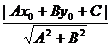 ;
;
(2)两平行直线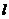 1:
1: 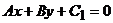 ,
,
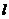 2:
2: 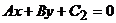 之间的距离d=
之间的距离d=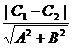 .
.
6.怎么判断两直线是否平行或垂直?判断两直线是否平行或垂直时,若两直线的斜率都存在,可以用斜率的关系来判断;若直线的斜率不存在,则必须用一般式的平行垂直条件来判断.
(1)斜率存在且不重合的两条直线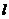 1∶
1∶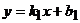 ,
,
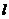 2∶
2∶ ,有以下结论:
,有以下结论:
①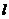 1∥
1∥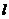 2
2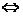
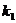 =
=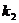 ,且b1=b2
,且b1=b2
②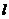 1⊥
1⊥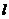 2
2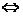
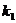 ·
·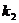 = -1
= -1
(2)对于直线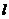 1∶
1∶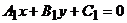 ,
,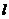 2 ∶
2 ∶ ,当
,当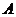 1,
1,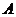 2,
2,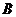 1,
1,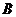 2都不为零时,有以下结论:
2都不为零时,有以下结论:
①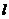 1∥
1∥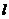 2
2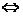
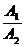 =
=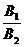 ≠
≠
②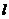 1⊥
1⊥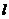 2
2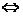
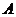 1
1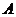 2+
2+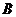 1
1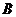 2
= 0
2
= 0
③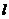 1与
1与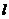 2相交
2相交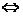
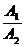 ≠
≠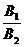
④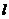 1与
1与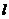 2重合
2重合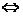
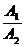 =
=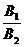 =
=
5.两条直线的夹角。当两直线的斜率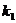 ,
,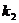 都存在且
都存在且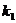 ·
·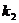 ≠ -1时,tanθ=
≠ -1时,tanθ=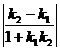 ,当直线的斜率不存在时,可结合图形判断.另外还应注意到:“到角”公式与“夹角”公式的区别.
,当直线的斜率不存在时,可结合图形判断.另外还应注意到:“到角”公式与“夹角”公式的区别.
4.确定直线方程需要有两个互相独立的条件。直线方程的形式很多,但必须注意各种形式的直线方程的适用范围.
|
名称 |
方程 |
说明 |
适用条件 |
|
斜截式 |
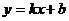 |
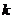 为直线的斜率 为直线的斜率b为直线的纵截距 |
倾斜角为90°的直线不能用此式 |
|
点斜式 |
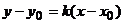 |
(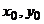 )
为直线上的已知点, )
为直线上的已知点,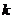 为直线的斜率 为直线的斜率 |
倾斜角为90°的直线不能用此式 |
|
两点式 |
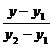 = =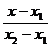 |
(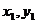 ),( ),(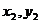 )是直线上两个已知点 )是直线上两个已知点 |
与两坐标轴平行的直线不能用此式 |
|
截距式 |
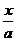 + + =1 =1 |
 为直线的横截距 为直线的横截距b为直线的纵截距 |
过(0,0)及与两坐标轴平行的直线不能用此式 |
|
一般式 |
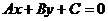 |
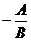 , ,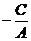 , ,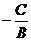 分别为斜率、横截距和纵截距 分别为斜率、横截距和纵截距 |
A、B不全为零 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com