
21、设a为实数,记函数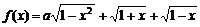 的最大值为g(a)。
的最大值为g(a)。
(Ⅰ)设t=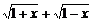 ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)
(Ⅱ)求g(a)
20、解:(1)设P(x0,y0)是y=f(x)图象上点,Q(x,y),则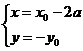 ,
,
∴ ∴-y=loga(x+2a-3a),∴y=loga
∴-y=loga(x+2a-3a),∴y=loga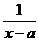 (x>a)
(x>a)
(2)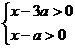 ∴x>3a
∴x>3a
∵f(x)与g(x)在[a+2,a+3]上有意义. ∴3a<a+2 ∴0<a<1
∵|f(x)-g(x)|≤1恒成立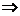 |loga(x-3a)(x-a)|≤1恒成立.
|loga(x-3a)(x-a)|≤1恒成立.
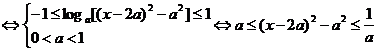
对x∈[a+2,a+3]上恒成立,令h(x)=(x-2a)2-a2
其对称轴x=2a,2a<2,2<a+2 ∴当x∈[a+2,a+3]
hmin(x)=h(a+2),hmax=h(a+3)
∴原问题等价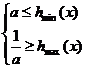
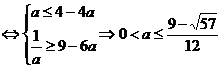
20、函数f(x)=loga(x-3a)(a>0,且a≠1),当点P(x,y)是函数y=f(x)图象上的点时,
Q(x-2a,-y)是函数y=g(x)图象上的点.
⑴写出函数y=g(x)的解析式. ⑵当x∈[a+2,a+3]时,恒有|f(x)-g(x)|≤1,试确定a的取值范围.
19、解:(1)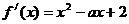 ,由题知:
,由题知: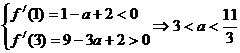 ;
;
(2)由(1)知: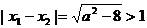 ,
,
∴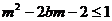 对
对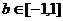 恒成立,所以:
恒成立,所以: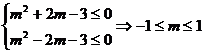
19、已知函数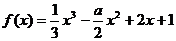 且
且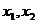 是
是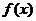 的两个极值点,
的两个极值点,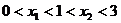 ,
,
(Ⅰ)求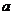 的取值范围;
的取值范围;
(Ⅱ)若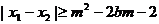 ,对
,对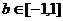 恒成立。求实数
恒成立。求实数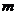 的取值范围
的取值范围
18、解:(Ⅰ)∵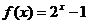 ∴
∴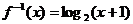 (x>-1)
(x>-1)
由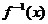 ≤g(x) ∴
≤g(x) ∴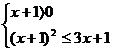 解得0≤x≤1 ∴D=[0,1]
解得0≤x≤1 ∴D=[0,1]
(Ⅱ)H(x)=g(x)-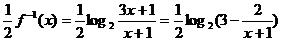
∵0≤x≤1 ∴1≤3-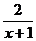 ≤2 ∴0≤H(x)≤
≤2 ∴0≤H(x)≤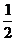 ∴H(x)的值域为[0,
∴H(x)的值域为[0,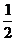 ]
]
18、已知f(x)=2x-1的反函数为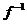 (x),g(x)=log4(3x+1).
(x),g(x)=log4(3x+1).
⑴若f-1(x)≤g(x),求x的取值范围D;
⑵设函数H(x)=g(x)-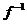 (x),当x∈D时,求函数H(x)的值域
(x),当x∈D时,求函数H(x)的值域
17、解: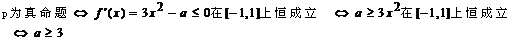
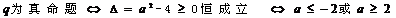
由题意P和q有且只有一个是真命题
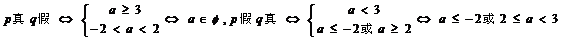 综上所述:
综上所述: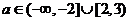
17、设命题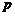 :函数f(x)=x3-ax-1在区间
:函数f(x)=x3-ax-1在区间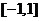 上单调递减;命题
上单调递减;命题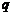 :函数
:函数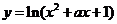 的值域是R.如果命题
的值域是R.如果命题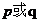 为真命题,
为真命题,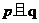 为假命题,求
为假命题,求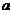 的取值范围.
的取值范围.
16、已知函数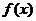 的定义域为R,则下列命题中:
的定义域为R,则下列命题中:
①若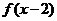 是偶函数,则函数
是偶函数,则函数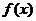 的图象关于直线x=2对称;
的图象关于直线x=2对称;
②若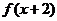 =-
=-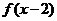 ,则函数
,则函数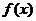 的图象关于原点对称;
的图象关于原点对称;
③函数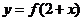 与函数
与函数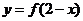 的图象关于直线x=2对称;
的图象关于直线x=2对称;
④函数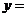
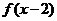 与函数
与函数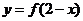 的图象关于直线x=2对称.
的图象关于直线x=2对称.
其中正确的命题序号是 .④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com