6.最小值

f(x)是闭区间［a，b］上的连续函数，如果对于任意x∈［a，b］，f(x₂)≤f(x)，那么f(x)在点x₂处有最小值f(x₂).

由图我们可以知道，函数f(x)在［a，b］上连续，则一定有最大最小值，这是闭区间上连续函数的一个性质.最大，最小值可以在(a，b)内的点取到，也可以在a，b两个端点上取到.

5.最大值

f(x)是闭区间［a，b］上的连续函数，如果对于任意x∈［a，b］，f(x₁)≥f(x)，那么f(x)在点x₁处有最大值f(x₁).

4.函数f(x)在［a，b］上连续的定义：

如果f(x)在开区间(a，b)内连续，在左端点x=a处有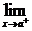f(x)=f(a)，在右端点x=b处有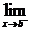f(x)=f(b),就说函数f(x)在闭区间［a，b］上连续,或f(x)是闭区间［a，b］上的连续函数.

如果函数f(x)在闭区间［a，b］上是连续函数，那它的图象肯定是一条连续曲线.

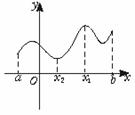
我们来看这张图，它是连续的，在a、b两点的值都是取到，所以它一定有一个最高点和一个最低点，假设在x₁这点最高；那么它的函数值最大，就是说［a，b］区间上的各个点的值都不大于x₁处的值，用数学语言表示就是f(x₁)≥f(x)，x∈［a，b］，同理，设x₂是最低点，f(x₂)≤f(x)，x∈［a，b］.

3.函数f(x)在(a，b)内连续的定义：

如果函数f(x)在某一开区间(a，b)内每一点处连续，就说函数f(x)在开区间(a，b)内连续，或f(x)是开区间(a，b)内的连续函数.

f(x)在开区间(a，b)内的每一点以及在a、b两点都连续，现在函数f(x)的定义域是［a，b］，若在a点连续，则f(x)在a点的极限存在并且等于f(a)，即在a点的左、右极限都存在，且都等于f(a)， f(x)在(a，b)内的每一点处连续，在a点处右极限存在等于f(a)，在b点处左极限存在等于f(b).

2. 函数在一点连续的定义: 如果函数f(x)在点x=x₀处有定义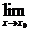，f(x)存在，且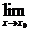f(x)=f(x₀)，那么函数f(x)在点x=x₀处连续.

由第三个条件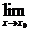，f(x)=f(x₀)就可以知道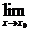f(x)是存在的，所以我们下定义时可以再简洁一点. 函数f(x)在点x₀处连续的定义.

如果函数y=f(x)在点x=x₀处及其附近有定义，并且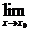f(x)=f(x₀)，就说函数f(x)在点x₀处连续.

那怎么根据在一点连续的定义来定义在一个开区间(a，b)内连续的定义．　区间是由点构成的，只要函数f(x)在开区间内的每一个点都连续，那么它在开区间内也就连续了.

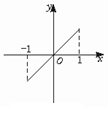
1.观察图像 如果我们给出一个函数的图象，从直观上看，一个函数在一点x=x₀处连续，就是说图象在点x=x₀处是不中断的.下面我们一起来看一下几张函数图象，并观察一下，它们在x=x₀处的连续情况，以及极限情况.

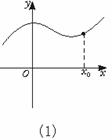
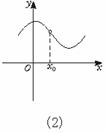
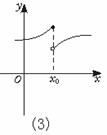
分析图，第一，看函数在x₀是否连续.第二，在x₀是否有极限，若有与f(x₀)的值关系如何：

图(1)，函数在x₀连续，在x₀处有极限，并且极限就等于f(x₀).

图(2)，函数在x₀不连续，在x₀处有极限，但极限不等于f(x₀)，因为函数在x₀处没有定义.

图(3)，函数在x₀不连续，在x₀处没有极限.

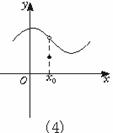
图(4)，函数在x₀处不连续，在x₀处有极限，但极限不等于f(x₀)的值.

函数在点x=x₀处要有定义，是根据图(2)得到的，根据图(3)，函数在x=x₀处要有极限，根据图(4)，函数在x=x₀处的极限要等于函数在x=x₀处的函数值即f(x₀).　函数在一点连续必须满足刚才的三个条件.

.函数f(x)在点x=x₀处连续必须满足下面三个条件.

(1)函数f(x)在点x=x₀处有定义；

(2)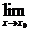f(x)存在；

(3)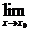f(x)=f(x₀)，即函数f(x)在点x₀处的极限值等于这一点的函数值.

如果上述三个条件中有一个条件不满足，就说函数f(x)在点x₀处不连续.那根据这三个条件，我们就可以给出函数在一点连续的定义．

2. 我们前面学习了数列极限和函数极限、数列可以看成是一种特殊的函数，不同的是函数的定义域往往是连续的.而数列的定义域是自然数集，是一个一个离散的点.而在我们日常生活中，也会碰到这种情况.比如温度计的水银柱高度会随着温度的改变而连续地上升或下降，这是一种连续变化的情况；再比如邮寄信件的邮费，随邮件质量的增加而作阶梯式的增加(打个比方：20克以内是8毛钱邮票，21克~30克是1元，31克~40克是1.2元)等等.这就要求我们去研究函数的连续与不连续问题

1.

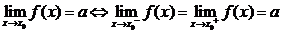
其中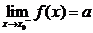表示当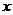从左侧趋近于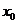时的左极限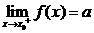，表示当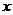从右侧趋近于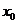时的右极限

15、(2010·南开中学模拟)三氧化二铁和氧化亚铜都是红色粉末，常用作颜料。某校一化学实验小组通过实验来探究一红色粉末是Fe₂O₃、Cu₂O或二者混合物。探究过程如下：

查阅资料：Cu₂O是一种碱性氧化物, 溶于稀硫酸生成Cu和CuSO₄, 在空气中加热生成CuO

提出假设

假设1：红色粉末是Fe₂O₃

假设2：红色粉末是Cu₂O

假设3：红色粉末是Fe₂O₃和Cu₂O的混合物

设计探究实验

取少量粉末放入足量稀硫酸中，在所得溶液中再滴加 KSCN 试剂。

(1)若假设1成立，则实验现象是　　　　　　　　　　　　 。

(2)若滴加 KSCN 试剂后溶液不变红色，则证明原固体粉末中一定不含三氧化二铁。你认为这种说法合理吗？　　　　　 简述你的理由(不需写出反应的方程式 )　　　　　　　　　　　　　　 。

(3)若固体粉末完全溶解无固体存在 , 滴加 KSCN 试剂时溶液不变红色 , 则证明原固体粉末是　　　　　 ，写出发生反应的离子方程式　　　　　　　　　　　　　　　　　　　　　 。

探究延伸

经实验分析，确定红色粉末为Fe₂O₃和Cu₂O的混合物。

(4)实验小组欲用加热法测定Cu₂O的质量分数。取a g固体粉末在空气中充分加热，待质量不再变化时，称其质量为bg( b > a)，则混合物中Cu₂O的质量分数为　　　　 。

(5)实验小组欲利用该红色粉末制取较纯净的胆矾 (CuS0₄ . 5H₂0) 。经查阅资料得知 ,

在溶液中通过调节溶液的酸碱性而使Cu^{2 +}、Fe²⁺、Fe³⁺分别生成沉淀的pH 如下：

实验室有下列试剂可供选择：A. 氯水　 B. H₂O₂ 　　C. NaOH　 D. Cu_­2(OH)₂CO₃

实验小组设计如下实验方案：

试回答：

① 试剂I为　　　 ，试剂II为　　　 (填字母)。

② 固体X的化学式为　　　　　 。

③ 操作I为　　　　　　　　　 。

[解析](1)若假设1成立，则溶液中含有Fe³⁺，遇到KSCN溶液呈红色。

(2)如果混合物中含有Cu₂O，遇到酸产生Cu，Cu能与Fe³⁺反应，故此种说法不正确。

(3)若固体全部溶解，则一定存在Fe₂O₃和Cu₂O，因为Cu₂O溶于硫酸生成Cu和CuSO₄，而H₂SO₄不能溶解Cu，所以混合物中必须有Fe₂O₃存在，使其生成的Fe³⁺溶解产生的Cu。

(4)依据题意，能发生反应的物质为Cu₂O，最后变成CuO，增加的质量就是反应的氧气的质量，根据质量差计算可以得出Cu₂O的质量分数。

(5)根据表格可知，Fe(OH)₃完全沉淀时，pH最小，故应将Fe²⁺先转化为Fe³⁺，在利用增大pH的方法除去溶液中的Fe³⁺，但是所加物质不能增加新的杂质，故第一步氧化剂应是H₂O₂，再加入Cu_­2(OH)₂CO₃，调节pH，使溶液中的Fe³⁺生成沉淀除去。

[答案] (1)溶液变为血红色

(2)不合理　 Cu能将Fe³⁺还原为Fe²⁺

(3)Fe₂O₃和Cu₂O的混合物　 Fe₂O₃+6H⁺ = 2Fe³⁺+3H₂O　 Cu₂O+2H⁺ = Cu + Cu²⁺ + H₂O

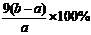2 Fe³⁺ + Cu = 2 Fe²⁺ + Cu²⁺

(4)　　　　　　　 　

(5)① B　 D　 ② Fe(OH)₃　 ③加热蒸发

()

14、(2010·许昌模拟)已知A为中学化学中的一种盐，B、C为日常生活中常见的金属.通常条件下D、G为无色无味气体.已知用惰性电极电解A溶液一段时间后，产物只有C、D和E的稀溶液.各物质之间的转化关系如下图(部分反应产物已略去).

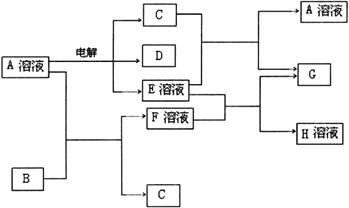
请回答下列问题：

(1)A的化学式为______________.

(2)A溶液与Na₂O₂反应的总化学方程式为______________________________.

(3)E的稀溶液与F溶液反应的离子方程式为_____________________________.

(4)电解100mL盐A的溶液一段时间后，断开电路，取出电极，测得所得到的气体D在标准状况下的体积为5.6mL，则电解后溶液的pH为__________.(假设溶液体积不变)

(5)若向100mL盐A的溶液中加入10g金属单质B的粉末，充分搅拌后，过滤，烘干得10.16g固体C.则滤液中溶质的物质的量浓度为__________.(假设溶液体积不变)

[答案](1)Cu(NO₃)₂

(2)2Na₂O₂+2Cu(NO₃)₂+2H₂O=2Cu(OH)₂↓+4NaNO₃+O₂↑

(3)3Fe²⁺+NO₃^－+4H⁺==3Fe³⁺+NO↑+2H₂O

(4)2　　　 (5)0.2mol/L