1．此题为力学电学综合题，解题关键是电压表读数为CD两端的电压再由U_AB与U_CD的关系和受力分析求解。

3．故障分析方法

(1)仪器检测法：①断点故障的判断：用电压表与电源并联，若有电压时，再逐段与电路并联，若电压表指针偏转，则该段电路有断点。②短路故障的判断：用电压表与电源并联，若有电压时，再逐段与电路并联，若电压表示数为零，则该电路短路。

(2)假设法：已知电路发生某种故障，寻求故障发生在何处时，可将整个电路划分为若干部分，然后逐一假设某部分电路发生故障，运用有关规律进行推导，结果若与题设现象不符合，则此段无故障，否则可能发生在这部分电路，照此下去找到故障。

(3)排除法：在明确电路结构的基础上，从分析比较故障前后电路中电流、电压的变化人手，确立故障原因并对电路中元件逐一分析，排除不可能的情况，寻找故障所在。故障前后电路的两种状态，可根据不同状态物理量间的关系来求解有关量。

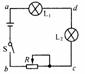[应用3]如图所示的电路中，电源电动势为6V，当开关S接通后，灯泡L₁和L₂都不亮，用电压表测得各部分电压是U_ab＝6V，U_ad＝0，U_dc＝6V，由此可判定(　　 )

A．L₁和L₂的灯丝都烧断了　 B．L₁的灯丝烧断了

C．L₂的灯丝烧断了　　　　 D．变阻器R断路

导示: 由题目给出的条件可知，电路中有的地方有电压，说明电源是有电压的。由U_ab＝6V和U_ad＝0可知外电路上bcd段有断点；由U_dc＝6V可知外电路上cL₂d段有断点，即L₂烧断，而且除L₂外，L₁和变阻器R都没有与L₂同时断开，否则也不存在U_dc＝6 V。在这种情况下，U_ad＝0是情理之中的。故而C选项正确。

类型一电路与力学综合问题分析

[例1]如图所示是一种悬球式加速度仪，它可以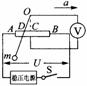用来测定沿水平轨道运动列车的加速度。m是一个金属球，它系在金属丝下端，金属丝的上端悬挂在O点，AB是一根长为L的电阻丝，其阻值为R₀金属丝与电阻丝接触良好，摩擦不计，电阻丝的中点C焊接一根导线。从O点也引出一根导线，两线之间接一个电压表V(金属丝和导线电阻不计)；图中虚线OC与AB垂直，且OC＝h，电阻丝AB接在电压为U的直流稳压电源上，整个装置固定在列车中使AB沿着前进的方向，列车静止时金属丝呈竖直状态，当列车加速或减速前进时，金属丝将偏离竖直方向，从电压表的读数变化可以测出加速度的大小。(1)当列车向右匀加速运动时，试写出加速度a与电压表U的对应关系?以便重新刻制电压表表面使它成为直读加速度数值的加速计。(2)用此装置测得的最大加速度是多少?(3)为什么C点设置在电阻丝AB的中间?对电压表的选择有什么特殊要求?

导示: (1)设列车加速度为a时悬挂小球的金属丝偏离竖直方向θ角，这时小球受到的合外力F＝mgtanθ，根据牛顿第二定律F＝ma得这时的加速度表达式为a＝gtanθ。因为tanθ＝DC/h将此式代入上式得a＝gDC/h ，就是触点D的位移跟加速度的关系式。

2．故障特点

(1)断路的特点：电源的电压不为零而电流强度为零，若外电路中任意两点间电压不为零，则这两点间有断点。

(2)短路的特点：有电流通过电路而电压为零。

1．故障电路的工作状态　

(1)断路状态：外电阻R→∞时，I＝0，U_外＝E，P_总＝P_出＝P_损＝0

(2)短路状态：外电阻R＝0时，I_短＝E/r，U_外＝0，P_总＝I_短E=E²/r，P_出＝0，P_损＝P_总

3．电路的电流、电压变化时，将会引起电容器的充(放)电。如果电容器两端电压升高，电容器将充电；如果电压降低，电容器将通过与它并联的电路放电。

[应用2](03全国江苏)在如图所示的电路中，电源的电动势E＝3.0 V，内阻r＝1.0Ω；电阻R₁＝10Ω，R₂＝10Ω，R₃＝30Ω．R₄＝35Ω；电容器的电容C＝100μF。电容器原来不带电。求接通电键K后流过R₄的总电荷量。

导示: 电路稳定时，直流电路中的电容器可视为开路，所以K接通电路稳定后，电路结构是电阻R₂与R₃串联，再与R₁并联。

由电阻的串并联公式，得闭合电路的总电阻为

知识点三故障电路分析

2．当电容器和电阻并联后接人电路时，电容器两极板间的电压与其并联在电阻两端的电压相等。

1．电路稳定后，由于电容器所在支路无电流通过。所以在此支路中的电阻上无电压降，因此电容器两极板间的电压就等于该支路两端的电压。

3．极限法：即因变阻器滑片滑动引起电路变化的问题,可将变阻器的滑动端分别滑至两个极端讨论。

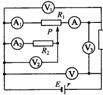[应用1]如图所示电路中，R₂、R₃是定值电阻．R₁是滑动变阻器，当R₁的滑键P向右滑动时，各个电表的示数怎样变化?

导示: 当R₁的滑键P向右滑动时，由R_l和R₂组成的分压器的串联电阻减小，所以电路的总电阻减小；根据I=E/(R+r)可知干路中的电流增大，电流表A的示数增大，再根据U＝E一Ir，可知路端电压减小，电压表V的示数减小。

因为R₃为定值电阻，当干路中电流增大时，其两端电压随之增大，所以电压表V₃的示数增大。根据U₁＝U一U₃，因U减小，U₃增大，所以U_l减小，电压表V₁的示数减小。

当滑动变阻器的滑键向右滑动时，R₁的左段电阻R_左与R₂并联部分的电阻增大，且干路中的电流增大，根据部分电路欧姆定律，可知电压表V₂的示数增大，由于R₂为定值电阻，且U₂增大，根据部分电路欧姆定律，可知电流表A₂示数增大。

根据并联分流原理，通过电流表A₁的电流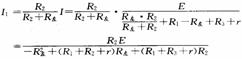

在上式中，分子为恒量，分母为关于R_左的二次函数，且二次项的系数小于零，分母有极大值，由此可见．电流表A₁的示数先减小后增大。

答案：V₁示数变小，V₂的示数增大，V₃的示数增大，V的示数减小，A₂示数增大，A₁示数先减小后增大。

对电路的动态分析，既能考查电路的结构，也能考查对闭合电路的理解和应用，一直是高考热点，基本的方法是通过分析部分电路的电阻变化，来分析其他电路的变化，在分析时注意程序：局部→整体→局部的思想，必要时可进行假设或由结果(答案)去逆向分析。

知识点二含容电路分析

电容器是一个储存电能的元件。在直流电路中，当电容器充放电时，电路中有充放电电流，一旦电路达到稳定状态，电容器在电路中就相当于断路，简化电路时可去掉它。简化后若要求电容器所带电荷量时，可在相应的位置补上。分析和计算含有电容器的直流电路时，需注意以下几点：

2．用“并同串反”规律判断：所渭“并同”，即某一电阻增大(减小)时，与它并联或间接并联的电阻中的电流、两端电压、电功率都将增大(减小)。所谓“串反”，即某一电阻增大时，与它串联或间接串联的电阻中的电流、两端电压，电功率都将减小。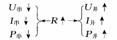

1．程序法：基本思路是“部分→整体→部分”，即从阻值变化的部分人手，由串并联规律判知R_总的变化情况，再由欧姆定律判知I_总和U_端的变化情况，最后由部分电路欧姆定律判知各部分物理量的变化情况，其一般思路为：

(1)确定电路的外电阻R_外总如何变化；

(2)根据闭合电路欧姆定律I_总=E/(R_外+r)确定电路的总电流如何变化(利用电动势不变)；

(3)由U_内＝I_总r确定电源内电压变化(利用r不变)；

(4)由U_外＝E-U内确定电源的外电压(路端电压)如何变化；

(5)由部分电路欧姆定律确定干路上某定值电阻两端的电压如何变化；

(6)由部分电路和整体的串并联规律确定支路两端电压如何变化以及通过各支路的电流如何变化。