
21.已知函数 (1)若
(1)若 在
在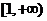 上单调递增,求
上单调递增,求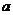 的取值范围;(2)若定义在区间D上的函数
的取值范围;(2)若定义在区间D上的函数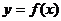 对于区间
对于区间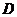 上的任意两个值
上的任意两个值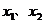 总有以下不等式
总有以下不等式 成立,则称函数
成立,则称函数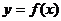 为区间
为区间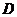 上的
上的
“凹函数”.试证:当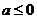 时,
时, 为“凹函数”.
为“凹函数”.
解(1)由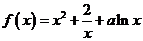 ,得
,得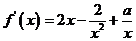 ……………………2分
……………………2分
函数为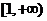 上单调函数. 若函数为
上单调函数. 若函数为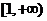 上单调增函数,则
上单调增函数,则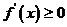 在
在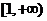 上恒成立,即不等式
上恒成立,即不等式 在
在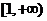 上恒成立. 也即
上恒成立. 也即 在
在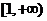 上恒成立. …………4分令
上恒成立. …………4分令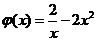 ,上述问题等价于
,上述问题等价于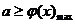 ,而
,而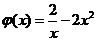 为在
为在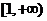 上的减函数,则
上的减函数,则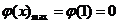 ,于是
,于是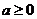 为所求. …………6分
为所求. …………6分
(2)证明:由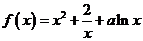 得
得
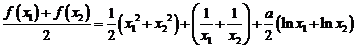
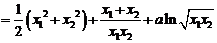 ………………………7分
………………………7分
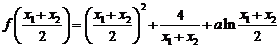 ……………………8分
……………………8分
而 ① ………………10分
① ………………10分
又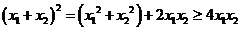 , ∴
, ∴ ② ………11分
② ………11分
∵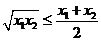 ∴
∴ ,
,
∵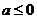 ∴
∴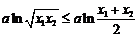 ③ ……………………………13分
③ ……………………………13分
由①、②、③得
即 ,从而由凹函数的定义可知函数为凹函数. …………14分
,从而由凹函数的定义可知函数为凹函数. …………14分
20.已知函数 .
.
(1)求函数 的单调区间;
的单调区间;
(2)设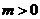 ,求
,求 在
在 上的最大值;
上的最大值;
(3)试证明:对任意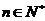 ,不等式
,不等式 恒成立.
恒成立.
解:(1)∵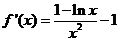
令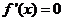 得
得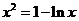
显然 是上方程的解
是上方程的解
令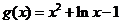 ,
,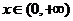 ,则
,则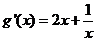

∴函数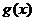 在
在 上单调递增
上单调递增
∴ 是方程
是方程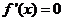 的唯一解
的唯一解
∵当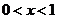 时
时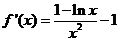
 ,当
,当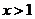 时
时
∴函数 在
在 上单调递增,在
上单调递增,在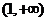 上单调递减………………5分
上单调递减………………5分
(2)由(1)知函数 在
在 上单调递增,在
上单调递增,在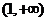 上单调递减
上单调递减
故①当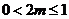 即
即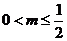 时
时 在
在 上单调递增
上单调递增
∴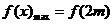 =
=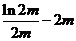
②当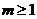 时
时 在
在 上单调递减
上单调递减
∴ =
=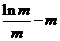
③当 ,即
,即 时
时
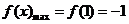 ……………………………………………………10分
……………………………………………………10分
(3)由(1)知当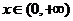 时,
时,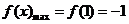
∴在 上恒有
上恒有
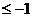 ,当且仅当
,当且仅当 时“=”成立
时“=”成立
∴对任意的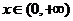 恒有
恒有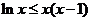
∵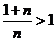 ∴
∴
即对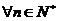 ,不等式
,不等式 恒成立.………………………14分
恒成立.………………………14分
19.已知函数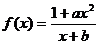
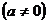 是奇函数,并且函数
是奇函数,并且函数 的图像经过点(1,3),
的图像经过点(1,3),
(1)求实数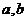 的值;(2)求函数
的值;(2)求函数 的值域
的值域
解:(1)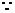 函数
函数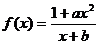 是奇函数,则
是奇函数,则
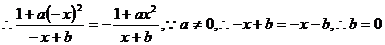 ………(3分)
………(3分)
又函数 的图像经过点(1,3),
的图像经过点(1,3),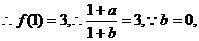 ∴a=2 ……(6分)
∴a=2 ……(6分)
(2)由(1)知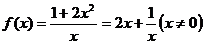 ………(7分)
………(7分)
当 时,
时,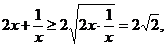 当且仅当
当且仅当
即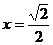 时取等号…(10分)
时取等号…(10分)
当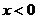 时,
时,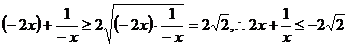
当且仅当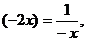 即
即 时取等号……………(12分)
时取等号……………(12分)
综上可知函数 的值域为
的值域为 …………(13分)
…………(13分)
18.5.12四川汶川大地震,牵动了全国各地人民的心,为了安置广 大灾民,抗震救灾指挥部决定建造一批简易房(每套长方体状,房高2.5米),前后墙用2.5米高的彩色钢板,两侧用2.5米高的复合钢板,两种钢板的价格都用长度来计算(即:钢板的高均为2.5米,用钢板的长度乘以单价就是这块钢板的价格),每米单价:彩色钢板为450元,复合钢板为200元.房顶用其它材料建造,每平方米材料费为200元.每套房材料费控制在32000元以内,试计算:
大灾民,抗震救灾指挥部决定建造一批简易房(每套长方体状,房高2.5米),前后墙用2.5米高的彩色钢板,两侧用2.5米高的复合钢板,两种钢板的价格都用长度来计算(即:钢板的高均为2.5米,用钢板的长度乘以单价就是这块钢板的价格),每米单价:彩色钢板为450元,复合钢板为200元.房顶用其它材料建造,每平方米材料费为200元.每套房材料费控制在32000元以内,试计算:
(1)设房前面墙的长为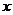 ,两侧墙的长为
,两侧墙的长为 ,所用材料费为
,所用材料费为 ,试用
,试用 表示
表示 ;
;
(2)求简易房面积S的最大值是多少?并求S最大时,前面墙的长度应设计为多少米?
解:(1)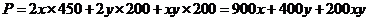 ……… 3分
……… 3分
即 ……………………… 6分
……………………… 6分
(2)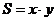 ,且
,且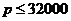 ;
;
由题意可得: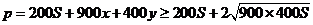 ………… 8分
………… 8分
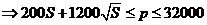

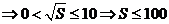 ;
…………………………………………… 10分
;
…………………………………………… 10分
当且仅当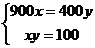
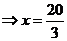 取最大值 ;
…………………………12分
取最大值 ;
…………………………12分
答:简易房面积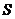 的最大值为100平方米,此时前面墙设计为
的最大值为100平方米,此时前面墙设计为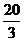 米. …… 13分
米. …… 13分
17.已知函数f(x)=5sinxcosx-5cos2x+.(x∈R),(1)求f(x)的最小正周期;
(2)求f(x)的单调区间;(3) 若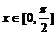 ,求
,求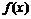 的最大值、最小值.
的最大值、最小值.
解:f(x)=sin2x-(1+cos2x)+=5sin(2x-)...4分∴(1)T=π.----5分
(2)令2kπ―≤2x―≤2kπ+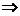 在[kπ-,kπ+](k∈Z)上单增,----7分
在[kπ-,kπ+](k∈Z)上单增,----7分
在[kπ+, kπ+π](k∈Z)上单减.----9分
(3)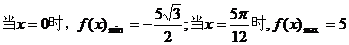 ----13分
----13分
16.已知集合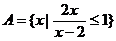 ,集合
,集合
(1)求集合 ;(2)若
;(2)若 ,求
,求 的取值范围。
的取值范围。
解析:(1) 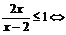
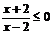 ----2分
----2分
 即A={x|
即A={x| }
--------6分
}
--------6分

 ------8分
------8分
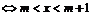 即A={x|
即A={x|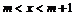 } ---------10分
} ---------10分
(2) B A
A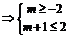
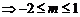 --------------------------13分
--------------------------13分
15.某商场国庆期间搞促销活动,规定:顾客购物总金额不超过500元,不享受任何折扣,如果顾客购物总金额超过500元,则超过500元部分享受一定的折扣优惠,按下表折扣分别累计计算:
|
可以享受折扣优惠金额 |
折扣率 |
|
不超过200元的部分 |
5% |
|
超过200元的部分 |
10% |
某人在此商场购物获得的折扣金额为35元,则他购物实际所付金额为 元915
14.若函数f(x)=log2(x2-ax+3a)在区间[2,+∞)上是增函数,则实数a的
取值范围是________.(-4<a≤4)
13.已知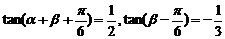 ,则
,则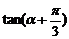 =_______________1
=_______________1
10.已知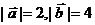 ,且
,且 与
与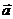 垂直,则
垂直,则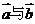 的夹角是_ __.(120度)
的夹角是_ __.(120度)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com