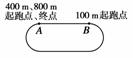
7．某学校田径运动场跑道示意图如右图所示，其中A点是所有跑步项目的终点，也是400 m、800 m赛跑的起跑点；B点是100 m赛跑的起跑点．在校运会中，甲、乙、丙三个同学分别参加了100 m、400　 m和800 m赛跑，则(　)

A．甲的位移最小 　　　　　　B．丙的位移最大

C．乙、丙的路程相等　　　 　D．丙的路程最大

[答案]　D

6.某一运动质点沿一直线往返运动，如右图所示，OA＝AB＝OC＝CD＝1 m，设O点为x轴坐标原点，且质点由A点出发向x轴的正方向运动至B点再返回沿x轴的负方向运动，则下列说法中正确的是(　)

A．质点在A→B→C时间内发生的位移为2 m，路程为4 m

B．质点在B→D时间内发生的位移为－4 m，路程为4 m

C．当质点运动到D点时，其位置可用D点的坐标－2 m表示

D．当质点运动到D点时，相对于出发点A的位移为－3 m

[答案]　BCD

5．如右图所示，某质点沿半径为r的半圆弧由a点运动到b点，则它通过的位移和路程分别是(　)

A．0；πr　 　　　　　　　B．2r，向东；πr

C．r，向东；πr 　　　　D．2r，向东；2r

[解析]　位移是指从初位置指向末位置的有向线段，只与初末位置有关，与运动径迹无关；而路程是指实际经过的径迹的长度，不仅与初末位置有关，还与运动径迹有关．

[答案]　B

4．某物体在水平面上向正南方向运动了30 m，然后又向正东方向运动了40 m，对于这一路程，下列说法正确的是(　)

A．物体的位移大小是50 m

B．物体的位移大小是70 m

C．物体的路程是50 m

D．物体的路程是70 m

[答案]　AD

3．某人先向东走2 m，接着向西走6 m，最后向南走3 m，则他在这段运动中的位移大小和路程分别是(　)

A．5 m,5 m 　　　　　　B．11 m,11 m

C．5 m,11 m　 　　　　　D．11 m,5 m

[答案]　C

2．一个小球从距地面4 m高处落下，被地面弹回，在距地面1 m高处被接住．坐标原点定在抛出点正下方2 m处，向下方向为坐标轴的正方向．则小球的抛出点、落地点、接住点的位置坐标分别是 (　)

A．2 m，－2 m，－1 m　　B．－2 m,2 m,1 m

C．4 m,0,1 m　 　　　　　　D．－4 m,0，－1 m

[解析]　根据题意建立如右图所示的坐标系，0抛出点，坐标为－2 m，B点为坐标原点，D点为地面，坐标为2 m，C点为接住点，坐标为1 m，所以选项B正确．

[答案]　B

1．关于位移和路程，下列说法正确的是(　)

A．沿直线运动的物体，位移和路程是相等的

B．质点沿不同的路径由A到B，路程可能不同而位移一定相同

C．质点通过一段路程，其位移可能为零

D．质点运动位移的大小可能大于路程

[解析]　由于位移是矢量，而路程是标量，如果质点沿直线运动且没有往复时，位移与路程只是大小相等，若有往复，其大小也不相等，故A错；由于位移只与初、末位置有关，与路径无关，故B正确；若质点沿曲线运动一个过程之后又回到出发点时，位移为零，在任何情况下质点的位移都不可能大于路程，故C正确，D错．

[答案]　BC

2.位置变化的描述--位移

(本栏目内容，学生用书中以活页形式分册装订成册！)

15.

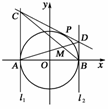
如右图，圆O：x²+y²=16与x轴交于A、B两点，l₁、l₂是分别过A、B点的⊙O的切线，过此圆上的另一点P(P点是圆上任一不与A、B重合的点)作此圆的切线，分别交l₁、l₂于C、D点，且AD、BC两直线的交点为M.

(1)当P点运动时，求切点M的轨迹方程；

(2)判断是否存在点Q(a,0)(a>0)使得Q点到轨迹上的点的最近距离为.若存在，求出所有这样的点Q；若不存在，请说明理由．

解：(1)设P(x₀，y₀)，M(x，y)，则x+y＝16，切线CD为x₀x+y₀y＝16.

由A(－4,0)，B(4,0)，得C(－4，)，

D(4，)．

∴直线AD：y＝(x+4)，直线BC：y＝－(x－4)，联立解得

代入x+y＝16，得x²+4y²＝16.

∵点P与A、B都不重合，∴y≠0.

故所求的轨迹方程是x²+4y²＝16(y≠0)．

(2)存在．

假设存在满足条件的点Q(a,0)，则d＝＝(－4<x<4)，

则当－4<a<4，即0<a<3时，

d_min＝＝，解得a＝.

当a≥3时，因为－4<x<4，此时d不存在最小值．

综上，存在这样的点Q，其坐标为(，0)．

14．已知圆C：x²+y²－2x+4y－4＝0，问是否存在斜率是1的直线l，使l被圆C截得的弦AB，以AB为直径的圆经过原点，若存在，写出直线l的方程；若不存在，说明理由．

解：假设存在直线l满足题设条件，设l的方程为y＝x+m，圆C化为(x－1)²+(y+2)²＝9，圆心C(1，－2)，则AB中点N是两直线x－y+m＝0与y+2＝－(x－1)的交点即N(－，)，以AB为直径的圆经过原点，

∴|AN|＝|ON|，又CN⊥AB，|CN|＝，

∴|AN|＝.

又|ON|＝，

由|AN|＝|ON|，解得m＝－4或m＝1.

∴存在直线l，其方程为y＝x－4或y＝x+1.