
1.在曲线y=x2+1的图象上取一点(1,2)及邻近一点(1+Δx,2+Δy),则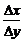 为( )
为( )
A.Δx+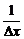 +2 B.Δx-
+2 B.Δx-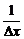 -2 C.Δx+2 D.2+Δx-
-2 C.Δx+2 D.2+Δx-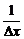
9.求导数的方法:
(1)求导公式; (2)导数的四则运算法则;
(3)复合函数的求导公式; (4)导数定义.
8.复合函数的导数:设函数u=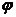 (x)在点x处有导数u′x=
(x)在点x处有导数u′x=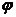 ′(x),函数y=f(u)在点x的对应点u处有导数y′u=f′(u),则复合函数y=f(
′(x),函数y=f(u)在点x的对应点u处有导数y′u=f′(u),则复合函数y=f(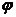 (x))在点x处也有导数,且
(x))在点x处也有导数,且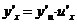 或
或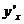 =f′(u)
=f′(u) 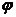 ′(x).
′(x).
7.导数的四则运算法则:
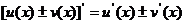 ;
; ;
;
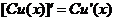 ;
;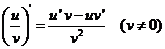

6.几种常见函数的导数:
 (C为常数);
(C为常数);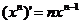 (
(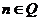 );
); ;
;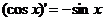 ;
;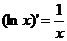 ;
;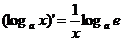 ;
;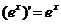 ;
;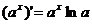 。
。
5.依定义求导数的方法:
 (1)求函数的改变量
(1)求函数的改变量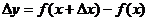
(2)求平均变化率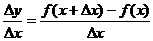
(3)取极限,得导数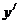 =
=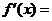

4.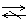 可导与连续的关系:如果函数y=f(x)在点x0处可导 函数y=f(x)在点x0处连续.
可导与连续的关系:如果函数y=f(x)在点x0处可导 函数y=f(x)在点x0处连续.
3.导函数、可导:如果函数y=f(x)在开区间(a,b)内的每点处都有导数,即对于每一个x∈(a,b),都对应着一个确定的导数f′(x0),从而构成了一个新的函数f′(x0), 称这个函数f′(x0)为函数y=f(x)在开区间内的导函数,简称导数。此时称函数y=f(x)在开区间(a,b)内可导.
2.导数的几何意义:函数y=f(x)在x0处的导数的几何意义,就是曲线y=f(x)在点(x0,y0)处的切线的斜率,即斜率为f′(x0).
过点P的切线方程为:y- y0= f′(x0) (x- x0).
1.导数的概念:设函数y=f(x)在x=x0处附近有定义,如果Δx→0时,Δy与Δx的比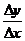 (也叫函数的平均变化率)有极限即
(也叫函数的平均变化率)有极限即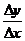 无限趋近于某个常数,我们把这个极限值叫做函数y=f(x)在Δx→0处的导数,记作
无限趋近于某个常数,我们把这个极限值叫做函数y=f(x)在Δx→0处的导数,记作
 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com