5. 若a是正实数，2a²+3b²=10，则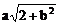的最大值等于________。

4.(2006陕西8) 已知不等式(x+y)( + )≥9对任意正实数x,y恒成立,则正实数a的最小值为　 ( 　　)

A　 2　 B　 4　　 C　 6　　 D　 8

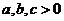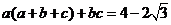3.(2006重庆)若且，则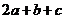的最小值为　 (　 )

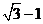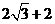(A)　　 　　　　 (B)　　 　　　 (C)　　 　 (D)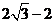

2．(2005福建)设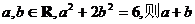的最小值是　 ( 　)

A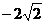．　　　　　　　 B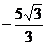．　　　　　　　 C．－3　　　 D．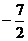

1. (2006浙江)“a>b>0”是”ab<”的　 (　 )

(A)充分而不必要条件　　　　　　　　　　　　　 (B)必要而不充分条件

(C)充分必要条件　　　　　　　　　　　　　 (D)既不充分也不必要条件

4．利用均值不等式可以证明不等式，求最值、取值范围，比较大小等。此外还要掌握如下常用不等式

;，

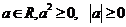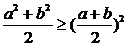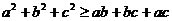
　若a>b>0,m>0,则 ；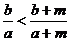

若a,b同号且a>b则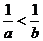,等。

3．最值定理:设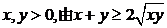

(1)如果x,y是正数,且积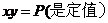,则xy时,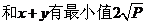

(2)如果x,y是正数和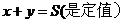,则x=y时,

运用最值定理求最值的三要素：一正二定三相等

1．基本不等式

(1)

(2)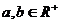，则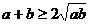

(3) 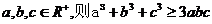,(拓展内容)

2 均值不等式:

两个正数的均值不等式：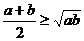

三个正数的均值不等是：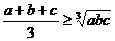

n个正数的均值不等式：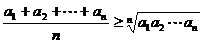

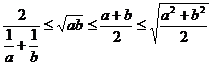
--两个正数的调和平均数、几何平均数、算术平均数、均方根之间的关系,这是一个非常重要的不等式,许多题目可以从中找到解题途径．

3.能运用均值定理来揭示数量间或实际问题中的不等关系.

2.会用平均值定理求最大或最小值;