2.如图所示，位于光滑水平桌面上的小滑块P和Q都可视作质点，质量相等。Q与轻质弹簧相连。设Q静止，P以某一初速度向Q运动并与弹簧发生碰撞。在整个碰撞过程中，弹簧具有的最大弹性势能等于

A.P的初动能　　　 B.P的初动能的1/2

C.P的初动能的1/3　　 D.P的初动能的1/4

1.一位质量为m的运动员从下蹲状态向上起跳，经Δt时间，身体伸直并刚好离开地面，速度为v。在此过程中，

A.地面对他的冲量为mv+mgΔt，地面对他做的功为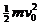

B.地面对他的冲量为mv+mgΔt，地面对他做的功为零

C.地面对他的冲量为mv，地面对他做的功为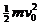

D.地面对他的冲量为mv－mgΔt，地面对他做的功为零

单质(1)+化合物(1)＝化合物(2)+单质(2)

请写出满足以下要求的3个置换反应的化学方程式：

①所涉及的元素的原子序数都小于20；　　 ②6种单质分别属6个不同的主族。

27、一个袋中装有大小相同的黑球、白球和红球，已知袋中共有10个球，从中任意摸出1个球，得到黑球的概率是;从中任意摸出2个球，至少得到1个白球的概率是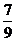.求：

(Ⅰ)从中任意摸出2个球，得到的都是黑球的概率；

(Ⅱ)袋中白球的个数。

26、甲、乙两个篮球运动员互不影响地在同一位置投球，命中率分别为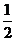与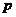，且乙投球2次均未命中的概率为．

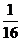(Ⅰ)求乙投球的命中率；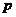

(Ⅱ)求甲投球2次，至少命中1次的概率；

(Ⅲ)若甲、乙两人各投球2次，求两人共命中2次的概率．

25、设进入某商场的每一位顾客购买甲种商品的概率位0.5，购买乙种商品的概率为0.6，且购买甲种商品与乙种商品相互独立，各顾客之间购买商品是相互独立的.

(Ⅰ)求进入该商场的1位顾客购买甲、乙两种商品中的一种的概率

(Ⅱ)求进入该商场的3位顾客中，至少有2位顾客既未购买甲种也未购买乙种商品的概率

24、某射击测试规则为：每人最多射击3次，击中目标即终止射击，第次击中目标得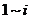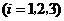分，3次均未击中目标得0分．已知某射手每次击中目标的概率为0.8，其各次射击结果互不影响．

(Ⅰ)求该射手恰好射击两次的概率；

(Ⅱ)该射手的得分记为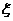，求随机变量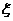的分布列及数学期望．

23、甲、乙、丙三人参加了一家公司的招聘面试，面试合格者可正式签约，甲表示只要面试合格就签约。乙、丙则约定：两人面试都合格就一同签约，否则两人都不签约。设每人面试合格的概率都是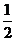，且面试是否合格互不影响。求：

(Ⅰ)至少有1人面试合格的概率;

(Ⅱ)签约人数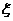的分布列和数学期望.

22、随机抽取某厂的某种产品200件，经质检，其中有一等品126件、二等品50件、三等品20件、次品4件．已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元，而1件次品亏损2万元．设1件产品的利润(单位：万元)为．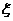

(1)求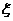的分布列；

(2)求1件产品的平均利润(即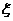的数学期望)；

(3)经技术革新后，仍有四个等级的产品，但次品率降为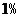，一等品率提高为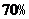．如果此时要求1件产品的平均利润不小于4.73万元，则三等品率最多是多少？

21、甲、乙等五名奥运志愿者被随机地分到四个不同的岗位服务，每个岗位至少有一名志愿者．

(Ⅰ)求甲、乙两人同时参加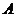岗位服务的概率；

(Ⅱ)求甲、乙两人不在同一个岗位服务的概率；

(Ⅲ)设随机变量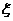为这五名志愿者中参加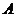岗位服务的人数，求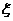的分布列．