7.一根1m长的小棒，第一次截去它的，第二次截去剩下的，如此截下去，第五次后剩下的小棒的长度是　　　　　　　　　　　　　 (　　 )

A .()⁵m　 　B. [1－()⁵]m　 　　C. ()⁵m　 　D. [1－()⁵]m

6．某粮店出售的三种品牌的面粉袋上分别标有质量为(25±0.1)kg,(25±0.2)kg, (25±0.3)kg的字样，从中任意拿出两袋，它们的质量最多相差　 (　　 )

A.0.8kg　 B.0.6kg　 C.0.5kg　 D.0.4kg　

5.若a+b＜0,ab＜0,则　　　　　　　　　　　　　 (　　 )

A.a＞0,b＞0;　

B.a＜0,b＜0;

C. a,b两数一正一负，且正数的绝对值大于负数的绝对值;

D.a,b两数一正一负，且负数的绝对值大于正数的绝对值

4.下列运算正确的是　　 　　　　　　　　　　　(　　 )

A.　　 B.－7－2×5=－9×5=－45

C.3÷　　　　 D.－(-3)²=-9

3.下列说法正确的是　　　　　　　　　　　　 (　　 )

①0是绝对值最小的有理数;　 ②相反数大于本身的数是负数;

③数轴上原点两侧的数互为相反数;　 ④两个数比较，绝对值大的反而小

A.①②　 B.①③　　 C.①②③　　 D.①②③④

2.a,b是有理数，它们在数轴上的对应点的位置如下图所示：

　　　　　　　　 a　　 0　　　　　　　 b

把a,-a,b,-b按照从小到大的顺序排列　　　　　　　　 (　　 )

A. -b＜-a＜a＜b　　 B.-a＜-b＜a＜b　　 C. -b＜a＜-a＜b　　 D.-b＜b＜-a＜a

1.下列说法正确的个数是　　　　　　　　 (　　 )

①一个有理数不是整数就是分数;　 ②一个有理数不是正数就是负数;

③一个整数不是正的，就是负的;　 ④一个分数不是正的，就是负的

　 　A.1　 B.2　 C.3　 D.4　

6.解：(1)函数f(x)在［－1，1］上是增函数.

证明：设任意x₁,x₂∈［－1,1］,且x₁<x₂.由于f(x)是定义在［－1，1］上的奇函数，∴f(x₂)－f(x₁)=f(x₂)+f(－x₁).　 因为x₁<x₂,所以x₂+(－x₁)≠0,由已知有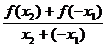＞0，∵x₂+(－x₁)=x₂－x₁>0∴f(x₂)+f(－x₁)>0,

即f(x₂)>f(x₁),所以函数f(x)在［－1，1］上是增函数.　　　　　　　　　　　　　

(2)由不等式f(x+)＜f()得

,解得－1<x<0,即为所求.　　　　　　　　　

(3)由以上知f(x)最大值为f(1)=1,所以要f(x)≤m²－2pm+1对所有x∈［－1,1］,p∈　　 ［－1,1］(p是常数)恒成立，只需1≤m²－2pm+1恒成立，得实数m的取值范围为m≤0或m≥2p.

1、　　　　2、　 3、C　 4、A　 5、　 6、C

例题选讲答案

1解析：又偶函数的性质知道：在上减，而，

，所以由得

，解得。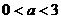

(设计理由：此类题源于变量与单调区间的分类讨论问题，所以本题弹性较大，可以作一些条件变换如：等；也可将定义域作一些调整)

2:解析：由易得是周期函数且周期为4。

，，所以

根据在时增，周期为4，区间与的单调性相同。

故。

(设计理由：此类题源于函数周期性与其他性质的结合题，因此题型的覆盖面可以表现于：1、周期性的表现形式：(1)或或等；(2)类似与三角的图象特征，具有两种对称的函数条件。如：

等。2、函数的周期性与其他函数性质的结合：解析式、单调性、对称性等。)

3:解析：

(设计理由：此类问题代表了以具体熟悉函数为背景函数的抽象函数的相关问题。此类问题可拓展到相关命题，让学生有一个整体的了解，同时抽象条件等式与函数性质的关联性的处理方法得以强化可规范。)

课后练习答案

1:　 　　2　 B　　　　　 3　 B　　　 4:x

6、已知f(x)是定义在［－1，1］上的奇函数，且f(1)=1,若a,b∈［－1,1］,a+b≠0时，有＞0.

(1)判断函数f(x)在［－1，1］上是增函数，还是减函数，并证明你的结论；

(2)解不等式：f(x+)＜f();

(3)若f(x)≤m²－2pm+1对所有x∈［－1,1］,p∈［－1,1］(p是常数)恒成立，求实数m的取值范围.

预习训练答案：