
10. (2005湖北)某地最近出台一项机动车驾照考试规定;每位考试者一年之内最多有4次参加考试的机会,一旦某次考试通过,便可领取驾照,不再参加以后的考试,否则就一直考到第4次为止。如果李明决定参加驾照考试,设他每次参加考试通过的概率依次为0.6,0.7,0.8,0.9,求在一年内李明参加驾照考试次数ξ的分布列和ξ的期望,并求李明在一年内领到驾照的概率.
解:ξ的取值分别为1,2,3,4.
ξ=1,表明李明第一次参加驾照考试就通过了,故P(ξ=1)=0.6.
ξ=2,表明李明在第一次考试未通过,第二次通过了,故
P(ξ=2)=(1-0.6)×0.7=0.28
ξ=3,表明李明在第一、二次考试未通过,第三次通过了,故
P(ξ=3)=(1-0.6)×(1-0.7)×0.8=0.096
ξ=4,表明李明第一、二、三次考试都未通过,故
P(ξ=4)=(1-0.6)×(1-0.7)×(1-0.8)=0.024
∴李明实际参加考试次数ξ的分布列为
|
ξ |
1 |
2 |
3 |
4 |
|
P |
0.6 |
0.28 |
0.096 |
0.024 |
∴ξ的期望Eξ=1×0.6+2×0.28+3×0.096+4×0.024=1.544.
李明在一年内领到驾照的概率为
9.(2006全国Ⅰ)A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验 每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效
每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效 若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组 设每只小白鼠服用A有效的概率为
若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组 设每只小白鼠服用A有效的概率为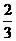 ,服用B有效的概率为
,服用B有效的概率为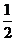 .
.
(Ⅰ)求一个试验组为甲类组的概率;
(Ⅱ)观察3个试验组,用ξ表示这3个试验组中甲类组的个数,求ξ的分布列和数学期望.
解:(Ⅰ)设Ai表示事件“一个试验组中,服用A有效的小白鼠有i只”,i=0,1,2, Bi表示事件“一个试验组中,服用B有效的小白鼠有i只”,i=0,1,2,依题意有
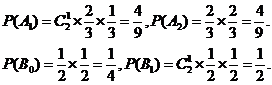
所求的概率为
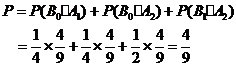
(Ⅱ)ξ的可能值为0,1,2,3且ξ~B(3,) 
P(ξ=0)=()3= , P(ξ=1)=C31××()2=,
P(ξ=2)=C32×()2× = , P(ξ=3)=( )3=
ξ的分布列为:
|
ξ |
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
数学期望: Eξ=3× =
8.(2006江西)某商场举行抽奖促销活动,抽奖规则是:从装有9个白球、1个红球的箱子中每次随机地摸出一个球,记下颜色后放回,摸出一个红球可获得奖金10元;摸出两个红球可获得奖金50元.现有甲、乙两位顾客,规定:甲摸一次,乙摸两次.令ξ表示甲、乙两人摸球后获得的奖金总额,求
(1) ξ的分布列; (2) ξ的数学期望.
.解: (1) ζ的所有可能的取值为0,10,20,50,60.
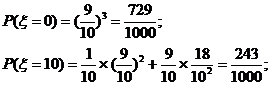

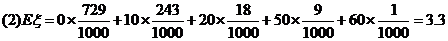 (元)
(元)
7.甲、乙乙两名射手在一次射击中,得分为两个独立的随机变量ξ和η,其分布列为
|
ξ |
1 |
2 |
3 |
|
P |
a |
0.1 |
0.6 |
|
η |
1 |
2 |
3 |
|
P |
0.3 |
b |
0.3 |
求(1)a,b的值;
(2)计算ξ、η的期望与方差,并据此分析甲、乙的技术状况。
解:(1)由a+0.1+0.6=1得a=0.7. 同理b=0.1
(2)Eξ=2.3, Eη=2.0 , Eξ>Eη
Dξ=0.81, Dη=0.6. Dξ>Dη
说明射击中甲的平均得分高于乙,但稳定性不如乙。
6.得分情况:4红得8分,3红1黑得7分,2红2黑得6分,1红3黑得5分.
故P(ξ=5)=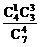 =
=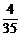 ,P(ξ=6)=
,P(ξ=6)=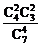 =
=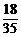 ,P(ξ=7)=
,P(ξ=7)=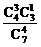 =
=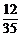 ,
,
P(ξ=8)=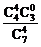 =
=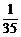 ,Eξ=5×
,Eξ=5×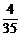 +6×
+6×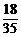 +7×
+7×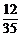 +8×
+8×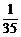 =
= =
=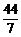 .
.
[解答题]
5.设甲答对题数为ξ,成绩为η,则ξ-B(50,0.8),η=2ξ,成绩的期望为Eη=E(2ξ)=2Eξ=2×50×0.8=80(分);
成绩的标准差为ση=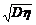 =
=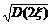 =
=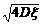 =2
=2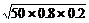 =4
=4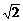 ≈5.7(分)
≈5.7(分)
4.Dξ=npq≤n(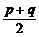 )2=
)2=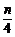 ,当p=q=
,当p=q=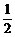 时等号成立,Dξ=25,σξ=5.答案:
时等号成立,Dξ=25,σξ=5.答案: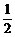 , 5.
, 5.
6.袋中有4个红球,3个黑球,今从袋中随机取出4个球.设取到一个红球得2分,取到一个黑球得1分,则得分ξ的取值为_____________,ξ数学期望等于__________.
◆练习简答:1-3.CAC;
5.一次单元测试由50个选择题构成,每个选择题有4个选项,其中恰有1个是正确答案.每题选择正确得2分,不选或错选得0分,满分是100分.学生甲选对任一题的概率为0.8,求他在这次测试中成绩的期望和标准差.
4.设一次试验成功的概率为p,进行100次独立重复试验,当p=________时,成功次数的标准差的值最大,其最大值为________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com