
2、考点解读
生物技术的安全性和伦理问题内容包括《转基因生物的安全性》、《关注生物技术的伦理问题》和《禁止生物武器》。本专题还安排了一个课外活动:“社会调查”(或“辩论会”)。
本部分的学习是在前面几个专题的基础上进行的。前面几个专题主要是在技术层面上介绍各种生物技术的原理与应用,其知识、技能的成分更多些,而本专题主要是进行安全性和伦理问题的讨论。例如,关于“转基因生物的安全性”问题的讨论。本专题最后一节,通过对生物武器的介绍,让学生了解生物武器的危害。在恐怖主义猖獗且现代生物技术迅速发展的今天,了解生物武器对人类的威胁,具有一定的现实意义。本部分之所以选取了与现代生物技术的发展直接相关的几个比较突出的问题进行讨论,主要的意图有以下几方面:
(1)提出在生命科学发展过程中,所引出的种种伦理、社会和法律问题。
(2)在学生已有的生命科学基础知识之上,引导学生对科技成果的应用进行正确的思考。
(3)要让学生了解,由于个人所处的社会在政治制度、经济发展水平、宗教信仰、历史背景、传统伦理观念等方面的差别,就会产生出不同价值观。这样,对于生命科学中同一个伦理、社会或法律问题,在不同社会中不仅会有不同的看法,而且还会引导出截然不同的社会措施、政策和法规。
(4)对于中国来说,所有的判断和所立的法规,都必须符合自己的国情,符合国家的最高利益:既要有利于中国科学家占领科学研究制高点、有利于国家科学技术的繁荣,又要有利于促进国家经济的发展。
另外,通过介绍我国对待转基因生物、治疗性克隆、生物武器等问题的政策和法规,使学生们认识到,生物技术立法要在国际法规的大框架下,符合自己的国情。
本部分学习中,学生要能够对生物技术的安全性和伦理问题进行一些反思和辨析,需要运用到基因工程、细胞工程,以及胚胎工程等现代生物技术的基础知识。因此,前三个专题的学习是本专题的基础。
生态工程内容包括《生态工程的基本原理》和《生态工程的实例和发展前景》。本专题还安排一个实践活动《调查沼气工程的实施情况》。
1、考点盘点
|
内容 |
说明 |
|
(1)转基因生物的安全问题;; (2)生物武器对人类的威胁;; (3)生物技术中的伦理问题; (4)生态工程的原理; (5)生态工程的实例 |
收集我国转基因食物安全性的监控和预防措施等方面的资料 举例说出转基因生物技术成果的实例 简述转基因生物与食物安全、生物安全和环境安全等方面的观点 参与转基因生物安全性的讨论和交流 尝试调查当地市场的转基因食物,或农村栽培或饲养的转基因生物 说出能充当生物武器的病原体 举例说出生物武器对人类的危害 举例说出生物技术的伦理问题 选择合适的角度,参与生物技术伦理问题的讨论 说出我国和国外关于生物技术使用的规定、立场或态度 说出生态工程与传统工程的差异 简述生态工程的主要原理,如物质循环再生原理、物种多样性原理、协调与平衡原理等 利用生态工程原理,分析、解释生态环境中出现的现象 收集当地或国内生态工程的实例 就某一生态工程实例,说出建立生态工程的原因、建立生态工程的流程和产生的效益 讨论生态工程发展的前景 调查当地某一生态工程的实施情况 |
12.三棱锥S-ABC中,一条棱长为a,其余棱长均为1,求a为何值时VS-ABC最大,并求最大值.
解 方法一 如图所示,
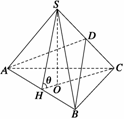 设SC=a,其余棱长均为1,
设SC=a,其余棱长均为1,
取AB的中点H,连接HS、HC,
则AB⊥HC,AB⊥HS,
∴AB⊥平面SHC.
在面SHC中,过S作SO⊥HC,则SO⊥平面ABC.
在△SAB中,SA=AB=BS=1,
∴SH= ,
,
设∠SHO= ,则SO=SHsin
,则SO=SHsin =
= sin
sin ,
,
∴VS-ABC=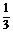 S△ABC·SO
S△ABC·SO
=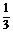 ×
×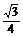 ×12×
×12× sin
sin
=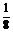 sin
sin ≤
≤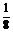 .
.
当且仅当sin =1,即
=1,即 =90°时,三棱锥的体积最大.
=90°时,三棱锥的体积最大.
a=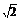 SH=
SH=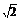 ×
× =
= ,Vmax=
,Vmax=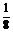 .
.
∴a为 时,三棱锥的体积最大为
时,三棱锥的体积最大为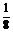 .
.
方法二 取SC的中点D,可通过VS-ABC=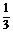 S△ABD·SC,转化为关于a的目标函数的最大值问题,利用基本不等式或配方法解决.
S△ABD·SC,转化为关于a的目标函数的最大值问题,利用基本不等式或配方法解决.
11.如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=1,BB1=2,
E是棱CC1上的点,且CE=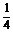 CC1.
CC1.
(1)求三棱锥C-BED的体积;
(2)求证:A1C⊥平面BDE.
(1)解 ∵CE=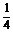 CC1=
CC1= ,
,
∴VC-BDE=VE-BCD=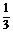 S△BCD·CE
S△BCD·CE
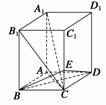 =
=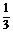 ×
× ×1×1×
×1×1× =
=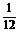 .
.
(2)证明 连接AC、B1C.
∵AB=BC,∴BD⊥AC.
∵A1A⊥底面ABCD,
∴BD⊥A1A.
∵A1A∩AC=A,
∴BD⊥平面A1AC.
∴BD⊥A1C.
∵tan∠BB1C=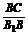 =
= ,
,
tan∠CBE=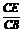 =
= ,∴∠BB1C=∠CBE.
,∴∠BB1C=∠CBE.
∵∠BB1C+∠BCB1=90°,
∴∠CBE+∠BCB1=90°,∴BE⊥B1C.
∵BE⊥A1B1,A1B1∩B1C=B1,
∴BE⊥平面A1B1C,∴BE⊥A1C.
∵BD∩BE=B,BE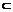 平面BDE,BD
平面BDE,BD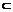 平面BDE,
平面BDE,
∴A1C⊥平面BDE.
10.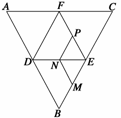 如图所示,正△ABC的边长为4,D、E、F分别为各边中点,M、N、P分别为BE、DE、EF的中点,将△ABC沿DE、EF、DF折成了三棱锥以后.
如图所示,正△ABC的边长为4,D、E、F分别为各边中点,M、N、P分别为BE、DE、EF的中点,将△ABC沿DE、EF、DF折成了三棱锥以后.
(1)∠MNP等于多少度?
(2)擦去线段EM、EN、EP后剩下的几何体是什么?其侧面积为多少?
解 (1)由题意,折成了三棱锥以后,如图所示,
△MNP为正三角形,故∠MNP=∠DAF=60°.
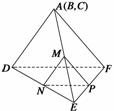
(2)擦去线段EM、EN、EP后,所得几何体为棱台,
其侧面积为S侧=SE-ADF侧-SE-MNP侧
 =3×
=3×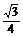 ×22-3×
×22-3×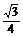 ×12=
×12=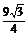 .
.
9.一个正三棱台的上、下底面边长分别是3 cm和6 cm,高是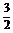 cm,
cm,
(1)求三棱台的斜高;
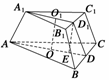 (2)求三棱台的侧面积和表面积.
(2)求三棱台的侧面积和表面积.
解 (1)设O1、O分别为正三棱台ABC-A1B1C1的上、下底面正三角形的中心,如图所示,
则O1O=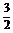 ,过O1作O1D1⊥B1C1,OD⊥BC,则D1D为三棱台的斜高;
,过O1作O1D1⊥B1C1,OD⊥BC,则D1D为三棱台的斜高;
过D1作D1E⊥AD于E,则D1E=O1O=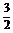 ,
,
因O1D1=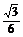 ×3=
×3= ,OD=
,OD=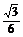 ×6=
×6=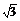 ,
,
则DE=OD-O1D1=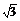 -
- =
= .
.
在Rt△D1DE中,
D1D=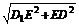 =
=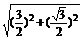 =
=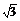 .
.
(2)设C、C′分别为上、下底的周长,h′为斜高,
S侧= (C+C′)h′=
(C+C′)h′= (3×3+3×6)×
(3×3+3×6)×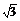 =
= (cm2),
(cm2),
S表=S侧+S上+S下= +
+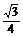 ×32+
×32+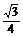 ×62=
×62=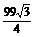 (cm2).
(cm2).
故三棱台斜高为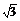 cm,侧面积为
cm,侧面积为 cm2,表面积为
cm2,表面积为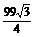 cm2.
cm2.
8.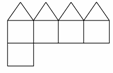 (2008·上海春招)已知一个凸多面体共有9个面,所有棱长均为1,其平面展开图如图所示,则该凸多面体的体积V=
.
(2008·上海春招)已知一个凸多面体共有9个面,所有棱长均为1,其平面展开图如图所示,则该凸多面体的体积V=
.
答案 1+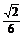
7.(2008·四川理,15)已知正四棱柱的对角线的长为 ,且对角线与底面所成角的余弦值为
,且对角线与底面所成角的余弦值为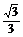 ,则该正四棱柱的体积等于
.
,则该正四棱柱的体积等于
.
答案 2
6.一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积
是 .
答案 
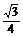
5.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是 .
答案 24
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com