
3.对于化学平衡的有关图象问题,可按以下的方法进行分析:
(1)认清坐标系,搞清纵、横坐标所代表的意义,并与勒沙特列原理挂钩。
(2)紧扣可逆反应的特征,搞清正反应方向是吸热还是放热,体积增大还是减小、不变,有无固体、纯液体物质参加或生成等。
(3)看清速率的变化及变化量的大小,在条件与变化之间搭桥。
(4)看清起点、拐点、终点,看清曲线的变化趋势。
(5)先拐先平。例如,在转化率-时间图上,先出现拐点的曲线先达到平衡,此时逆向推理可得该变化的温度高、浓度大、压强高。
(6)定一议二。当图象中有三个量时,先确定一个量不变再讨论另外两个量的关系。
试题枚举
[例1]某温度下,在体积为5L的容器中,A、B、C三种物质物质的量随着时间变化的关系如图1所示,则该反应的化学方程式为_________,2s内用A的浓度变化和用B的浓度变化表示的平均反应速率分别为_________、_________。
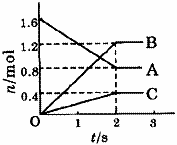 解析:这类题目是讨论同一时间段内各物质的变化量的比例关系,且要注意物质的量减少的为反应物,物质的量增多的为生成物。又因物质的量都不变时,反应物、生成物共存,故方程式要用“
解析:这类题目是讨论同一时间段内各物质的变化量的比例关系,且要注意物质的量减少的为反应物,物质的量增多的为生成物。又因物质的量都不变时,反应物、生成物共存,故方程式要用“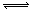 ”表示。
”表示。
答案:2A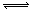 3B+C;0.08mol/(L·s);0.12mol/(L·s)。
3B+C;0.08mol/(L·s);0.12mol/(L·s)。
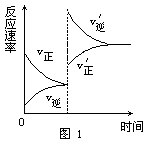
[例2] 对达到平衡状态的可逆反应X+Y Z+W,在其他条件不变的情况下,增大压强,反应速率变化图象如图1所示,则图象中关于X、Y、Z、W四种物质的聚集状态为
Z+W,在其他条件不变的情况下,增大压强,反应速率变化图象如图1所示,则图象中关于X、Y、Z、W四种物质的聚集状态为
 A.Z、W均为气体,X、Y中有一种是气体
A.Z、W均为气体,X、Y中有一种是气体
B.Z、W中有一种是气体,X、Y皆非气体
C.X、Y、Z、W皆非气体
D.X、Y均为气体,Z、W中有一种为气体
解析: 经常有一些同学错选B,认为增大压强,平衡向气体体积缩小的方向移动.其实,图象告诉我们的是:增大压强,加快了正、逆反应,但逆反应速率增大的幅度大于正反应速率增大的幅度,由此而导致平衡向左移动.而压强的改变,只影响气体反应的速率,选项B所言的X、Y皆非气体即其正反应速率不受影响,故正确答案为A.
答案:A
[例3]下列各图是温度(或压强)对应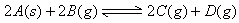 ;
;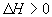 的正、逆反应速率的影响,曲线交点表示建立平衡时的温度或压强,其中正确的是
的正、逆反应速率的影响,曲线交点表示建立平衡时的温度或压强,其中正确的是
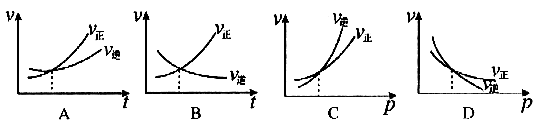
解析:曲线交点表示建立平衡时的温度或压强,升高温度,增加压强,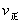 、
、 均增大,B中
均增大,B中 ,D中
,D中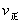 、
、 走向均减小,则B、D均错;可逆反应
走向均减小,则B、D均错;可逆反应 ;
;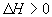 的正反应是一个气体体积增大的吸热反应,则升高温度,向正反应方向移动,故
的正反应是一个气体体积增大的吸热反应,则升高温度,向正反应方向移动,故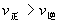 ;增加压强,向逆反应方向移动,故
;增加压强,向逆反应方向移动,故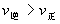 。
。
答案:A、C
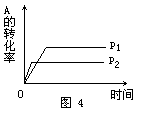
[例4] 现有可逆反应A(g)+2B(g) nC(g)+Q,在相同温度、不同压强时,A的转化率跟反应时间(t)的关系如图4,其中结论正确的是 [ ].
nC(g)+Q,在相同温度、不同压强时,A的转化率跟反应时间(t)的关系如图4,其中结论正确的是 [ ].
 A.p1>p2,n>3 B.p1<p2,n>3
A.p1>p2,n>3 B.p1<p2,n>3
C.p1<p2,n<3 D.p1>p2,n=3
解析: 当其他条件不变时,对于有气体参加的可逆反应,压强越大,到达平衡的时间越短.图象中曲线和横轴平行,表明反应已达平衡.由图象知道,当压强为p2时,该反应到达平衡的时间较短,故p1<p2.在其他条件不变的情况下,增大压强会使化学平衡向着气体体积缩小的方向移动.因p1<p2,且当压强为p1时,A的转化率较大,所以正反应为气体体积增加的反应,即1+2<n,故正确答案选B。
答案:B
2.对于化学反应速率的有关图象问题,可按以下的方法进行分析:
(1)认清坐标系,搞清纵、横坐标所代表的意义,并与有关的原理挂钩。
(2)看清起点,分清反应物、生成物,浓度减小的是反应物,浓度增大的是生成物一般生成物多数以原点为起点。
(3)抓住变化趋势,分清正、逆反应,吸、放热反应。升高温度时,v(吸)>v(放),在速率-时间图上,要注意看清曲线是连续的还是跳跃的,分清渐变和突变,大变和小变。例如,升高温度,v(吸)大增,v(放)小增,增大反应物浓度,v(正)突变,v(逆)渐变。
(4)注意终点。例如在浓度-时间图上,一定要看清终点时反应物的消耗量、生成物的增加量,并结合有关原理进行推理判断。
1.牢固掌握有关的概念与原理,尤其要注意外界条件的改变对一个可逆反应来讲,正逆反应速率如何变化,化学平衡如何移动,在速度-时间图、转化率-时间图、反应物的含量-浓度图等上如何体现。要能够画出有关的变化图象。
2.能够通过对图形、图表的观察,获取有关的感性知识和印象,并对这些感性知识进行初步加工和记忆
知识梳理
1.进一步掌握理解浓度、温度、压强、催化剂等条件对化学反应速率和化学平衡移动的影响。
2.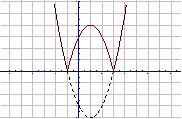 作出函数
作出函数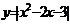 的函数图像
的函数图像
解: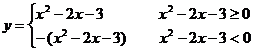
步骤:(1)作出函数y=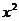 -2x-3的图象
-2x-3的图象
(2)将上述图象x轴下方部分以x轴为对称轴向上翻折(上方部分不变),即得y=|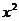 -2x-3|的图象
-2x-3|的图象
补充:
1.作函数y=|x-2|(x+1)的图像
分析 显然直接用已知函数的解析式列表描点有些困难,除去对其函数性质分析外,我们还应想到对已知解析式进行等价变形.
解:(1)当x≥2时,即x-2≥0时,
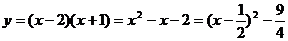
当x<2时,即x-2<0时,
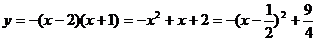 .
.
 ∴
∴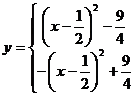

这是分段函数,每段函数图象可根据二次函数图象作出
例1某种笔记本每个5元,买 x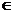 {1,2,3,4}个笔记本的钱数记为y(元),试写出以x为自变量的函数y的解析式,并画出这个函数的图像
{1,2,3,4}个笔记本的钱数记为y(元),试写出以x为自变量的函数y的解析式,并画出这个函数的图像
解:这个函数的定义域集合是{1,2,3,4},函数的解析式为
y=5x,x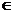 {1,2,3,4}.
{1,2,3,4}.
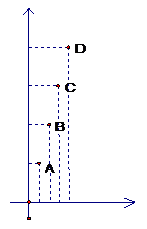
它的图象由4个孤立点A (1, 5) B (2, 10) C (3, 15) D
(4, 20)组成,如图所示
例2 国内投寄信函(外埠),每封信函不超过20g付邮资80分,超过20g而不超过40g付邮资160分,依次类推,每封x g(0<x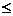 100)的信函应付邮资为(单位:分),试写出以x为自变量的函数y的解析式,并画出这个函数的图像
100)的信函应付邮资为(单位:分),试写出以x为自变量的函数y的解析式,并画出这个函数的图像
解:这个函数的定义域集合是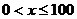 ,函数的解析式为
,函数的解析式为
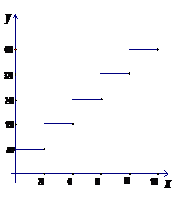
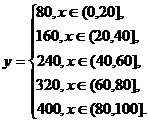
这个函数的图象是5条线段(不包括左端点),都平行于x轴,如图所示.
这一种函数我们把它称为分段函数
例3 画出函数y=|x|=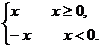 的图象.
的图象.
解:这个函数的图象是两条射线,分别是第一象限和第二象限的角平分线,如图所示.
说明:①再次说明函数图象的多样性;
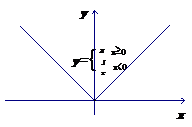 ②从例4和例5看到,有些函数在它的定义域中,对于自变量x的不同取值范围,对应法则不同,这样的函数通常称为分段函数.注意分段函数是一个函数,而不是几个函数.
②从例4和例5看到,有些函数在它的定义域中,对于自变量x的不同取值范围,对应法则不同,这样的函数通常称为分段函数.注意分段函数是一个函数,而不是几个函数.
③注意:并不是每一个函数都能作出它的图象,如狄利克雷(Dirichlet)函数D(x)=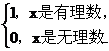 ,我们就作不出它的图象.
,我们就作不出它的图象.
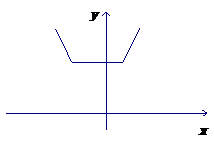
例4作出分段函数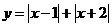 的图像
的图像
解:根据“零点分段法”去掉绝对值符号,即:
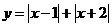 =
=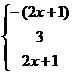
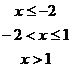
作出图像如下
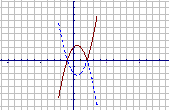
例5作出函数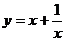 的图象
的图象
列表描点:

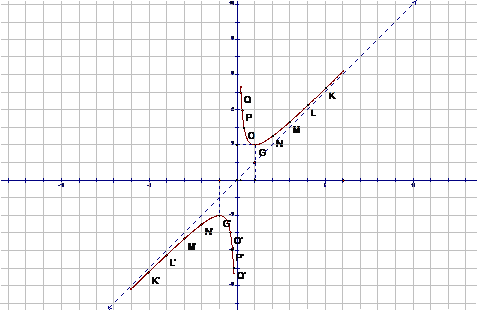
表示函数的方法,常用的有解析法、列表法和图象法三种.
⑴解析法:就是把两个变量的函数关系,用一个等式表示,这个等式叫做函数的解析表达式,简称解析式.
例如,s=60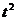 ,A=
,A=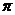
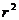 ,S=2
,S=2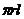 ,y=a
,y=a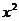 +bx+c(a
+bx+c(a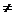 0),y=
0),y=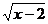 (x
(x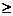 2)等等都是用解析式表示函数关系的.
2)等等都是用解析式表示函数关系的.
优点:一是简明、全面地概括了变量间的关系;二是可以通过解析式求出任意一个自变量的值所对应的函数值.中学阶段研究的函数主要是用解析法表示的函数.
⑵列表法:就是列出表格来表示两个变量的函数关系.
例如,学生的身高 单位:厘米
|
学号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
身高 |
125 |
135 |
140 |
156 |
138 |
172 |
167 |
158 |
169 |
数学用表中的平方表、平方根表、三角函数表,银行里的利息表,列车时刻表等等都是用列表法来表示函数关系的.公共汽车上的票价表
优点:不需要计算就可以直接看出与自变量的值相对应的函数值.
⑶图象法:就是用函数图象表示两个变量之间的关系.
 例如,气象台应用自动记录器描绘温度随时间变化的曲线,课本中我国人口出生率变化的曲线,工厂的生产图象,股市走向图等都是用图象法表示函数关系的.
例如,气象台应用自动记录器描绘温度随时间变化的曲线,课本中我国人口出生率变化的曲线,工厂的生产图象,股市走向图等都是用图象法表示函数关系的.
优点:能直观形象地表示出自变量的变化,相应的函数值变化的趋势,这样使得我们可以通过图象来研究函数的某些性质.
3.用描点法画函数图象,怎样避免描点前盲目列表计算?怎样做到描最少的点却能显示出图象的主要特征?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com