
10. 函数在一点连续的定义: 如果函数f(x)在点x=x0处有定义,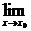 f(x)存在,且
f(x)存在,且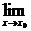 f(x)=f(x0),那么函数f(x)在点x=x0处连续.
f(x)=f(x0),那么函数f(x)在点x=x0处连续.
9. 数列极限的运算法则:
与函数极限的运算法则类似, 如果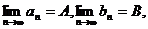 那么
那么
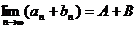

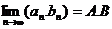
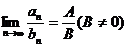

8. 对于函数极限有如下的运算法则:
如果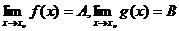 ,那么
,那么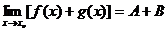 ,
,
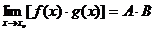 ,
, 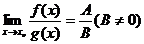

当C是常数,n是正整数时: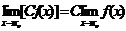 ,
,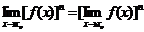
这些法则对于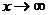 的情况仍然适用
的情况仍然适用 
7. 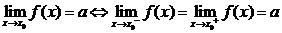
其中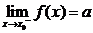 表示当
表示当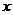 从左侧趋近于
从左侧趋近于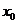 时的左极限,
时的左极限,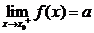 表示当
表示当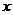 从右侧趋近于
从右侧趋近于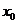 时的右极限
时的右极限 
6. 趋向于定值的函数极限概念:当自变量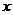 无限趋近于
无限趋近于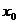 (
(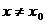 )时,如果函数
)时,如果函数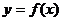 无限趋近于一个常数
无限趋近于一个常数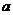 ,就说当
,就说当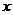 趋向
趋向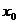 时,函数
时,函数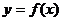 的极限是
的极限是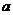 ,记作
,记作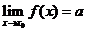
 特别地,
特别地,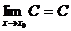 ;
;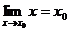

5.常数函数f(x)=c.(x∈R),有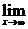 f(x)=c.
f(x)=c.
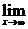 f(x)存在,表示
f(x)存在,表示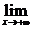 f(x)和
f(x)和 f(x)都存在,且两者相等.所以
f(x)都存在,且两者相等.所以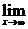 f(x)中的∞既有+∞,又有-∞的意义,而数列极限
f(x)中的∞既有+∞,又有-∞的意义,而数列极限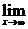 an中的∞仅有+∞的意义
an中的∞仅有+∞的意义

4.函数极限的定义:
(1)当自变量x取正值并且无限增大时,如果函数f(x)无限趋近于一个常数a,就说当x趋向于正无穷大时,函数f(x)的极限是a.
记作: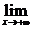 f(x)=a,或者当x→+∞时,f(x)→a.
f(x)=a,或者当x→+∞时,f(x)→a.
(2)当自变量x取负值并且绝对值无限增大时,如果函数f(x)无限趋近于一个常数a,就说当x趋向于负无穷大时,函数f(x)的极限是a.
记作 f(x)=a或者当x→-∞时,f(x)→a.
f(x)=a或者当x→-∞时,f(x)→a.
(3)如果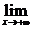 f(x)=a且
f(x)=a且 f(x)=a,那么就说当x趋向于无穷大时,函数f(x)的极限是a,记作:
f(x)=a,那么就说当x趋向于无穷大时,函数f(x)的极限是a,记作: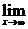 f(x)=a或者当x→∞时,f(x)→a.
f(x)=a或者当x→∞时,f(x)→a.
3.几个重要极限:
(1)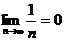 (2)
(2)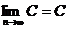 (C是常数)
(C是常数)
(3)无穷等比数列 (
(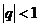 )的极限是0,即
)的极限是0,即 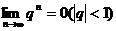

2.数列极限的定义:
一般地,如果当项数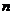 无限增大时,无穷数列
无限增大时,无穷数列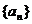 的项
的项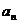 无限趋近于某个常数
无限趋近于某个常数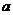 ,那么就说数列
,那么就说数列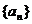 以
以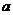 为极限.记作
为极限.记作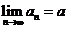 .
.
1.用数学归纳法证明一个与正整数n有关的命题的步骤:
(1)证明:当n取第一个值n0结论正确;
(2)假设当n=k(k∈N*,且k≥n0)时结论正确,证明当n=k+1时结论也正确.
由(1),(2)可知,命题对于从n0开始的所有正整数n都正确 
递推基础不可少,归纳假设要用到,结论写明莫忘掉 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com