
4.极限不存在的三种形态:①左极限不等于右极限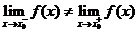 ;
;
②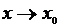 时,
时,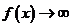 ,③
,③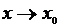 时,
时,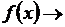 的值不确定。
的值不确定。
3.函数f(x)的左、右极限:
(1)如果当x从点x=x0左侧(即x<x0)无限趋近于x0时,函数f(x)无限趋近于常数a,就说a是函数f(x)的左极限,记作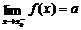 。
。
(2)同理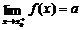 表示--
表示--
(3) 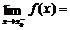
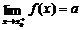
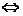
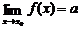 --判断函数在一点处极限存在的方法.
--判断函数在一点处极限存在的方法.
2.当x→x0时函数f(x)的极限:
当自变量x无限趋近于常数x0(从x0两侧,但x≠x0)时,如果函数f(x)无限趋近于一个常数a,就说当x趋向于x0时, 函数f(x)的极限是a,记作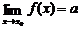 ,(或x→x0时,f(x)→a)
,(或x→x0时,f(x)→a)
(1)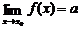 与函数f(x)在点x0处是否有定义及是否等于f(x0)都无关。
与函数f(x)在点x0处是否有定义及是否等于f(x0)都无关。
(2)“连续”函数在x0处的极限就等于 f(x0)
1.当x→∞时函数f(x)的极限:
(1)当自变量x取正值并且无限增大时,如果函数f(x)无限趋近于一个常数a,就说当x趋向于正无穷大时, 函数f(x)的极限是a,记作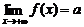 ,(或x→+∞时,f(x)→a)
,(或x→+∞时,f(x)→a)
(2)同理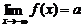 表示--
表示--
(3)当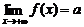 ,且
,且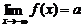 时,
时,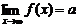
即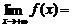
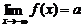
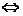
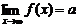
4.理解闭区间上连续函数有最大值和最小值的性质.
3.了解函数连续的意义;会判断简单函数的连续性;
2.掌握极限的四则运算法则;会求某些数列与函数的极限;
1.了解函数极限的概念;
44、读下图,完成下列问题。(12分)
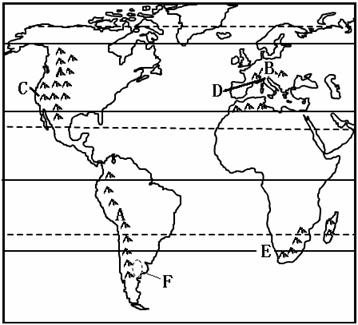
(1)运用板块构造学说理论分别说明图中山脉A、B的形成原因。
(2)图中新兴工业区的名称:C D 。
填表:比较两工业区
|
|
主要工业产品 |
科技水平高低 |
|
C处 |
○1 |
○2 |
|
D处 |
○3 |
○4 |
(3)E处附近有大范围渔场,分析其形成原因。
(4)F地区为巴塔哥尼亚荒漠,分析其形成原因。
43、根据图文资料,完成下列问题。(9分)
材料一:为了发挥区域优势,趋利避害,发展特色农业,增产增收。新疆地区的农民,充分利用种植瓜果的经验,引进山东蔬菜大棚技术,反季节生产新疆特色瓜果。下图为新疆某学校学生参加社会实践活动设计的改进型大棚示意图。
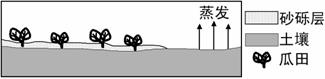
材料二:近年来,酒泉、兰州等地农民在瓜秧周围的表土上铺一些小石块,以提高西瓜的产量和质量,这就是“压砂技术”。如下图。
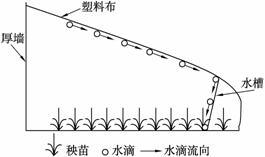
(1)利用大棚技术种植蔬菜,这种农业按产品的用途分类属于 ,按投入的多少分类属于 。
(2)改进型大棚的设计利用了 原理:地面、植物受到阳光照射,水分
或蒸腾到大棚顶部,水汽 成水滴,顺棚顶下滑到水槽,水滴沿水槽滴灌到秧苗根部。这一改进大大提高了 的利用率。
(3)请说明“压砂技术”能够提高瓜果产量和质量的主要原因。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com