
4.异面直线间的距离: .
3.两个平面的距离: .
2.直线到平面的距离: .
1.点到平面的距离: .
10.1+logx3与2logx2(x>0且x≠1)的大小.
解:(1+logx3)-2logx2=logx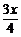 .
.
当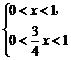 或
或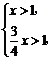
即0<x<1或x>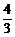 时,
时,
有logx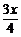 >0,1+logx3>2logx2.
>0,1+logx3>2logx2.
当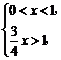 ①或
①或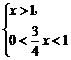 ②时,logx
②时,logx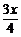 <0.
<0.
解①得无解,解②得1<x<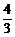 ,
,
即当1<x<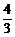 时,有logx
时,有logx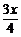 <0,
<0,
1+logx3<2logx2.
当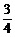 x=1,即x=
x=1,即x=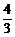 时,有logx
时,有logx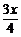 =0.
=0.
∴1+logx3=2logx2.
综上所述,当0<x<1或x>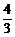 时,1+logx3>2logx2;
时,1+logx3>2logx2;
当1<x<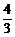 时,1+logx3<2logx2;
时,1+logx3<2logx2;
当x=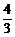 时,1+logx3=2logx2.
时,1+logx3=2logx2.
[探索题]x、y是正实数,记
A(x,y)=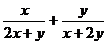 ,B(x,y)=
,B(x,y)=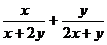
(1) 证明:A(x,y)≤B(x,y)
(2) 是否存在常数C,使得A(x,y)≤C≤B(x,y)恒成立?证明你的结论.
证明:(1)B(x,y)-A(x,y)=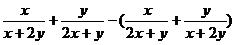
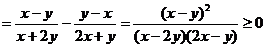
∴A(x,y)≤B(x,y).
(2)鉴于二式中关于x,y的轮换对称性,令x=y,得A(x,y)=B(x,y)=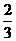
下证A(x,y)≤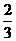 ≤B(x,y)
≤B(x,y)
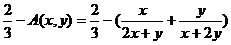
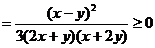
同理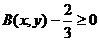 .
.
所以,存在正常数C=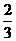 ,使A(x,y)≤C≤B(x,y)成立.
,使A(x,y)≤C≤B(x,y)成立.
(2)法2: (放缩法)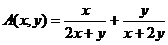
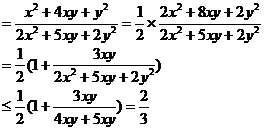
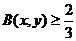
9.在等差数列{an}和等比数列{bn}中,a1=b1>0,a3=b3>0,a1≠a3.试比较下面两组数的大小.
(1) a2与b2.
(2) (2)a5与b5.
解:设an=a1+(n-1)d,bn=a1qn-1,依题意a1+2d=a1q2,∴d=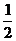 a1q2-
a1q2-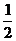 a1,
a1,
∴(1)a2-b2=a1+d-a1q=a1-a1q+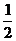 a1q2-
a1q2-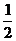 a1=
a1=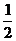 aq2-a1q+
aq2-a1q+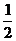 1=
1=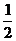 a(q-1)2,
a(q-1)2,
∵a1≠a3,∴a1≠a1+2d,即d≠0,q≠1,
∴a2-b2=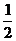 a1(q-1)2>0,∴a2>b2.
a1(q-1)2>0,∴a2>b2.
(2)a5-b5=a1+4d-a1q4=a1-a1q4+2a1q2-2a1=-a1q4+2a1q2-a1=-a1(q2-1)2<0,∴a5<b5.
8. 已知函数f(x)=x3+x 证明:
(1) f(x)是增函数;
(2) 若a,b,c∈R, 且,a+b>0,b+c>0,c+a>0,则f(a)+f(b)+f(c)>0.
证明:(1)设x1<x2
f(x1)-f(x2)=x13+x1-x23-x2
=(x1-x2)(x12+x1x2+x22+1) ①
当x1,x2同号时, ①=(x1-x2)[(x1-x2)2+3x1x2+1)]<0
当x1,x2异号时,①=(x1-x2)[(x1+x2)2-x1x2+1)]<0
综上有f(x1)<f(x2),故f(x)是增函数.
(2)∵f(-x)=-f(x), ∴f(x)是奇函数.又a+b>0即a>-b
∴f(a)>f(-b)=-f(b),即 f(a)+f(b)>0.
同理, f(b)+f(c)>0, f(a)+f(c)>0.
三式相加得2[f(a)+f(b)+f(c)]>0,所以f(a)+f(b)+f(c)>0成立.
7.设实数a,b,c满足①b+c=6-4a+3a2,②c-b=4-4a+a2,试确定a,b,c的大小关系.
解:∵c-b=(a-2)2≥0,∴c≥b,又2b=2+2a2,∴b=1+a2,∴b-a=a2-a+1=(a-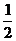 )2+
)2+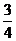 >0,∴b>a,从而c≥b>a.
>0,∴b>a,从而c≥b>a.
6.取特殊值a=-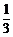 ,计算可得A=
,计算可得A=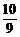 ,B=
,B=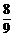 ,C=
,C=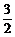 ,D=
,D=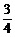 .
.
∴D<B<A<C.
[解答题]
5. 解:∵ab-(a+b)=(a-1)(b-1)-1>0.∴ab>a+b.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com