3、向心力表达式：

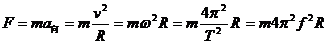
2、变速圆周运动特点：

(1)速度大小变化　　 有切向加速度；速度方向改变　　　 有向心加速度。故合加速度不一定指向圆心。

(2)合外力不一定全提供向心力，合外力不一定指向圆心。

目的要求

圆周运动向心力，牛顿第二定律的特定应用。

知识要点

1、匀速圆周运动特点：

(1)速度大小不变　　 无切向加速度；速度方向改变　　 有向心加速度a=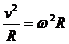

(2)合外力必提供向心力

2、描述匀速圆周运动的有关量及它们的关系：

(1)、线速度：

(2)、角速度：

(3)、周期：

(4)、频率：

(5)、向心加速度：

虽然匀速圆周运动线速度大小不变，但方向时刻改变，故匀速圆周运动是变速运动；向心加速度大小不变但方向时刻改变(始终指向圆心)，故匀速圆周运动是一种变加速运动。

例题分析

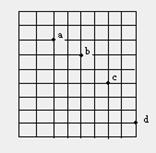
例1、如图所示为皮带传动装置，右轮半径为r，a为它边缘的一点，左侧是大轮轴，大轮半径为4r，小轮半径为2r。b为小轮上一点，它到小轮中心距离为r，c、d分别位于小轮和大轮的边缘上，若在传动中不打滑，则：(　 C　 D　 )

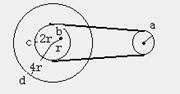　 A、a点与b点线速度大小相等；

B、a点与b点角速度大小相等；

C、a点与c点线速度大小相等；

D、a点与d点向心加速度大小相等；

本例主要考查线速度、角速度、向心加速度概念，同时抓住两个核心：若线速度一定时，角速度与半径成反比；若角速度一定，线速度与半径成正比。

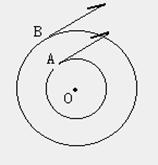　 例2、如图所示，A、B两质点绕同一圆心按顺时针方向作匀速圆周运动，A的周期为T₁，B的周期为T₂，且T₁＜T₂，在某时

刻两质点相距最近，开始计时，问：

(1)何时刻两质点相距又最近？

(2)何时刻两质点相距又最远？

分析：选取B为参照物。

(1)　　　 AB相距最近，则A相对于B转了n转，

其相对角度△Φ=2πn

相对角速度为ω_相=ω₁-ω₂经过时间：

t=△Φ/ω_相=2πn/ω₁-ω₂=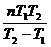 (n=1、2、3…)

(2)AB相距最远，则A相对于B转了n-1/2转，

其相对角度△Φ=2π(n-)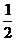

　　 经过时间：t=△Φ/ω_相=(2n-1)T₁T₂/2(T₂-T₁)(n=1、2、3…)

本题关键是弄清相距最近或最远需通过什么形式来联系A和B的问题，巧选参照系是解决这类难题的关键。

目的要求

学会利用描述匀速圆周运动有关物理量分析有关事例

知识要点

1、物体运动的轨迹是圆周或是圆周一部分叫圆周运动；作圆周运动的物体相等时间内通过的弧长相等称为匀速圆周运动。

[实验目的]

描述运动轨迹、求初速度

[实验原理]

利用水平方向匀速运动x=v₀t，竖直方向自由落体y=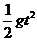　 得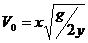测出多组x、y算出v₀值，再取平均值。

[实验器材]

平抛运动实验器材一套，刻度尺等。

[实验步骤]

见教材

[例题分析]

例1、如图所示，在研究平抛物体运动的实验中，用一张印有小方格的纸记录轨迹，小方格边长L=1.25cm,若小球在平抛运动途中的几个位置如图中的a,b,c,d。则小球平抛运动的初速度的计算式为v₀=(　　　　 )(用L g 表示).其值是(　　　　　 )(g=9.8m/s²)

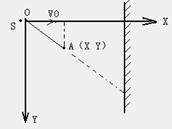
例2、房内高处有白炽灯S，可看成点光源，如果在S所在位置沿着垂直于墙的方向扔出一个小球A，如图所示，不计空气阻力，则A在墙上的影子的运动情况是( D　 )

A、加速度逐渐增大的直线运动，

B、加速度逐渐减小的直线运动

C、匀加速直线运动，

D、匀速直线运动。

例3、在“研究平抛运动”实验中，某同学只记录了小球运动途中的A、B、C三点的位置，取A点为坐标原点，则各点的位置坐标如图所示，下列说法正确的是：( B　 )

A、小球抛出点的位置坐标是(0，0)

B、小球抛出点的位置坐标是(-10，-5)

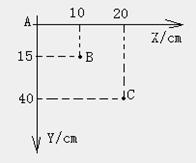　 C、小球平抛初速度为2m/s

D、小球平抛初速度为0.58m/s

2、平抛运动规律：(从抛出点开始计时)21世纪教育网

(1)、速度规律：　 V_X=V_{021世纪教育网}

V_Y=gt　 V与水平方向的夹角tgθ=gt/v_{021世纪教育网}

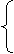(2)、位移规律：　 X=v₀t　　　　 (证明：轨迹是一条抛物线)21世纪教育网

Y=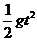　 S与水平方向的夹角tgα=gt/2v₀=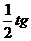θ21世纪教育网

(3)、平抛运动时间t与水平射程X21世纪教育网

　平抛运动时间t由高度Y决定，与初速度无关；水平射程X由初速度和高度共同决定。21世纪教育网

(4)、平抛运动中，任何两时刻的速度变化量△V=g△t(方向恒定向下)21世纪教育网

21世纪教育网

例题分析21世纪教育网

例1、一物体作平抛运动，它在落地前1秒内它的速度与水平方向的夹角由30⁰变成60⁰，①求平抛运动的初速度；②平抛运动的时间；③平抛运动高度。21世纪教育网

小结：研究和分析平抛运动，重在对两个分运动规律的理解和应用，即水平方向匀速直线运动，竖直方向自由落体运动规律的灵活交替运用。21世纪教育网

21世纪教育网

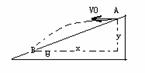　 例2、质点在斜面(倾角为θ)上以初速度V0水平抛出，落在斜面上B点，求飞行时间t?21世纪教育网

21世纪教育网

21世纪教育网

21世纪教育网

拓展1：上题中求质点运动到与斜面相距最远点所需时间t₁?(提示：抓住当速度与斜面平行时，质点与斜面相距最远这一特点)

拓展2：上题中求质点运动到与斜面相距最远点的距离H(灵活建立直角坐标系：平行斜面与垂直斜面建立)

拓展3：若质点以V₀正对倾角为θ的斜面水平抛出，落在斜面上时速度与斜面垂直，求飞行时间t₂？

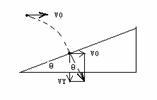
拓展4:若质点以V₀正对倾角为θ的斜面水平抛出,要求质点到达斜面的位移最小，求飞行时间t₃?(提示：连接抛出点O到斜面上的某点，其间距为位移大小，要使位移最小，只有落点在O₁且OO₁垂直于斜面即可。)

21世纪教育网

目的要求21世纪教育网

学会用运动分解的方法求解曲线运动。21世纪教育网

21世纪教育网

知识要点21世纪教育网

1、平抛运动特点：21世纪教育网

仅受重力作用，水平方向匀速直线运动，竖直方向自由落体，是一种匀变速曲线运动；轨迹是条抛物线。21世纪教育网

3、运动的合成与分解：21世纪教育网

运动的合成与分解包含了位移、加速度、速度的合成与分解。均遵循平行四边形法则。(一般采用正交分解法处理合运动与分运动的关系)中学阶段，运动的合成与分解是设法把曲线运动(正交)分解成直线运动再用直线运动规律求解。21世纪教育网

常见模型：　 船渡河问题；21世纪教育网

绳通过定滑轮拉物体运动问题21世纪教育网

21世纪教育网

例题分析21世纪教育网

例1、关于运动的合成与分解，下列说法正确的是：( BCD )21世纪教育网

A、两个直线运动的合运动一定是直线运动；21世纪教育网

B、两个互成角度的匀速直线运动的合运动一定是直线运动；21世纪教育网

C、两个匀加速运动的合运动可能是曲线运动；21世纪教育网

D两个初速为零的匀加速直线运动互成角度，合运动一定是匀加速直线运动；21世纪教育网

说明：本例题作为概念性判断题，可采用特例法解决。21世纪教育网

21世纪教育网

例2、河宽为d，水流速度为v1，船在静水中速度为v2，且v1＜v2，如果小船航向与河岸成θ角斜向上游，求：21世纪教育网

(1)它渡河需多少时间？21世纪教育网

(2)如果要以最短时间过河，船头应指向何方？此时渡河位移为多少？21世纪教育网

(3)如果要以最短位移渡河，船头应指向何方？此时渡河时间为多少？21世纪教育网

拓展：当v1＞v2时，讨论以上三问？21世纪教育网

21世纪教育网

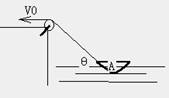
例3、如图在高出水面h的河岸上通过定滑轮用恒定速率v0拉绳，使船A靠岸，求当绳与水平夹角为θ时，船速VA为多大？根据结论说明靠岸过程中，船作什么性质运动？21世纪教育网

21世纪教育网

　 21世纪教育网

21世纪教育网

21世纪教育网

2、作曲线运动的条件：21世纪教育网

物体所受合外力与速度方向不在同一直线上。21世纪教育网

中学阶段实际处理的合外力与速度的关系常有以下三种情况：21世纪教育网

①、合外力为恒力，合外力与速度成某一角度，如在重力作用下平抛，带电粒子垂直进入匀强电场的类平抛等。21世纪教育网

②、合外力为变力，大小不变，仅方向变，且合外力与速度垂直，如匀速圆周运动。21世纪教育网

③、一般情误况，合外力既是变力，又与速度不垂直时，高中阶段只作定性分析。21世纪教育网