
1、对于给定的振动系统,振动的动能由振动的速度决定,振动的势能由振动的位移决定,振动的能量就是振动系统在某个状态下的动能和势能的总和.
5、小球在光滑圆弧上的往复滚动,和单摆完全等同。只要摆角足够小,这个振动就是简谐运动。这时周期公式中的l应该是圆弧半径R和小球半径r的差。
4、 单摆的周期:当 l、g一定,则周期为定值 T=2π
单摆的周期:当 l、g一定,则周期为定值 T=2π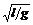 ,与小球是否运动无关.与摆球质量m、振幅A都无关。其中摆长l指悬点到小球重心的距离,重力加速度为单摆所在处的测量值。要区分摆长和摆线长。
,与小球是否运动无关.与摆球质量m、振幅A都无关。其中摆长l指悬点到小球重心的距离,重力加速度为单摆所在处的测量值。要区分摆长和摆线长。
3、单摆振动的回复力是重力的切向分力,不能说成是重力和拉力的合力。在平衡位置振子所受回复力是零,但合力是向心力,指向悬点,不为零。
2、单摆振动可看做简谐运动的条件是:在同一竖直面内摆动,摆角θ<100.
1、 单摆:在细线的一端挂上一个小球,另一端固定在悬点上,如果线的伸缩和质量可以忽略,球的直径比线长短得多,这样的装置叫做单摆.
单摆:在细线的一端挂上一个小球,另一端固定在悬点上,如果线的伸缩和质量可以忽略,球的直径比线长短得多,这样的装置叫做单摆.
这是一种理想化的模型,一般情况下细线(杆)下接一个小球的装置都可作为单摆.
3、利用振动图像分析简谐振动
[例7]一弹簧振子沿x轴振动,振幅为4 cm. 振子的平衡位置位于x袖上的0点.图甲中的a ,b,c,d为四个不同的振动状态:黑点表示振子的位置,黑点上箭头表示运动的方向.图乙给出的①②③④四条振动图线,
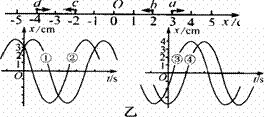 可用于表示振子的振动图象是( AD
)
可用于表示振子的振动图象是( AD
)
A.若规定状态a时t=0,则图象为①
B.若规定状态b时t=0,则图象为②
C.若规定状态c时t=0,则图象为③
D.若规定状态d时t=0,则图象为④
解析:若t=0,质点处于a状态,则此时x=+3 cm运动方向为正方向,只有图①对;若t=0时质点处于b状态,此时x=+2 cm,运动方向为负方向,②图不对;若取处于C状态时t=0,此时x=-2 cm,运动方向为负方向,故图③不正确;取状态d为t=0时,图④刚好符合,故A,D正确.
点评: 对振动图象的理解和掌握要密切联系实际,既能根据实际振动画出振动图象;又能根据振动图象还原成一个具体的振动,达到此种境界,就可熟练地用图象分析解决振动
试题展示
 单摆、振动中的能量
单摆、振动中的能量
知识简析 一、单摆
2、弹簧振子模型
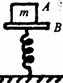 [例5]如图所示,质量为m的物块A放在木板B上,而B固定在竖直的轻弹簧上。若使
A随 B一起沿竖直方向做简谐运动而始终不脱离,则充当 A的回复力的是
。当A的速度达到最大时,A对B的压力大小为
。
[例5]如图所示,质量为m的物块A放在木板B上,而B固定在竖直的轻弹簧上。若使
A随 B一起沿竖直方向做简谐运动而始终不脱离,则充当 A的回复力的是
。当A的速度达到最大时,A对B的压力大小为
。
解析:根据题意,只要在最高点A、B仍能相对静止,则它们就会始终不脱离。而在最高点,外界对A所提供的最大回复力为mg,即最大加速度amax=g,故A、B不脱离的条件是a≤g,可见,在振动过程中,是A的重力和B对A的支持力的合力充当回复力。
因为A在系统的平衡位置时,速度最大,此时A所受重力与B对它的支持力的合力为零,由牛顿第三定律可知,a对B的压力大小等于其重力mg。
拓展:①要使不脱离B,其最大振幅为多少?可仍以最高点为例,设弹簧的劲度系数为k,B的质量为mB,因为mg=mamax,振幅最大时,a才有最大值,,是由kAmax=(m+mB)g,得Amax= m+mB)g/k。
②运动至最低点时A对B的最大压力是多少?③若让A从离静止的B上方h处自由下落与B相碰一起运动,则在最低点的加速度一定满足a>g,为什么?
[例6]在光滑的水平面上停放着一辆质量为M的小车,质量为m的物体与劲度系数为k的一轻弹簧固定相连.弹簧的另一端与小车左端固定连接,将弹簧压缩x0后用细绳将m 栓住,m静止在小车上的A点,如图所示,m与M 间的动摩擦因数为μ,O 点为弹簧原长位置,将细绳烧断后,m、M开始运动.求:①当m位于O点左侧还是右侧且跟O点多远时,小车的速度最大?并简要说明速度为最大的理由.②判断m与M的最终运动状态是静止、匀速运动还是相对往复的运动?
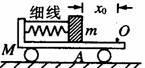 [解析]①在细线烧断时,小球受水平向左的弹力F与水平向右的摩擦力f作用,开始时F必大于f.m相对小车右移过程中,弹簧弹力减小,而小车所受摩擦力却不变,故小车做加速度减小的加速运动.当F=f时车速达到最大值,此时m必在O点左侧。设此时物体在O点左侧x处,则kx=μmg。所以,当x=μmg/k时,小车达最大速度.
[解析]①在细线烧断时,小球受水平向左的弹力F与水平向右的摩擦力f作用,开始时F必大于f.m相对小车右移过程中,弹簧弹力减小,而小车所受摩擦力却不变,故小车做加速度减小的加速运动.当F=f时车速达到最大值,此时m必在O点左侧。设此时物体在O点左侧x处,则kx=μmg。所以,当x=μmg/k时,小车达最大速度.
②小车向左运动达最大速度的时刻,物体向右运动也达最大速度,这时物体还会继续向右运动,但它的运动速度将减小,即小车和物体都在做振动.由于摩擦力的存在,小车和物体的振动幅度必定不断减小,设两物体最终有一共同速度v,因两物体组成的系统动量守恒,且初始状态的总动量为零,故v=0,即m与M的最终运动状态是静止的
4.应用:①可直观地读取振幅A、周期T以及各时刻的位移x;
②判定各时刻的回复力、速度、加速度方向;
③判定某段时间内位移、回复力、加速度、速度、动能、势能、等物理量的变化情况
注意:①振动图象不是质点的运动轨迹.
②计时点一旦确定,形状不变,仅随时间向后延伸。
③简谐运动图像的具体形状跟计时起点及正方向的规定有关。
规律方法1、简谐运动的特点
[例4](1995年全国)一弹簧振子作简谐振动,周期为T( )
A.若t时刻和(t+Δt)时刻振子运动位移的大小相等、方向相同,则Δt一定等于T的整数倍
B.若t时刻和(t+Δt)时刻振子运动速度的大小相等、方向相反,则上t一定等于T/2的整数倍
C.若Δt=T,则在 t时刻和(t+Δt)时刻振子运动的加速度一定相等
D.若Δt=T/2,则在t时刻和(t十Δt)时刻弹簧的长度一定相等
解析:做简谐运动时,振子由平衡位置到最大位移,再由最大位移回到平衡位置,两次经过同一点时,它们的位移大小相等、方向相同,其时间间隔并不等于周期的整数倍,选项A错误。同理在振子由指向最大位移,到反向最大位移的过程中,速度大小相等、方向相反的位里之间的时间间隔小于T/2,选项B错误。相差T/2的两个时刻,弹黄的长度可能相等,振子从平衡位置开始振动、再回到平衡位置时,弹簧长度相等、也可能不相等、选项D错误。若Δt=T,则根据周期性,该振子所有的物理量应和t时刻都相同,a就一定相等,所以,选项C正确。
本题也可通过振动图像分析出结果,请你自己尝试一下。
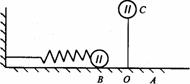 [例]如图所示,一弹簧振子在光滑水平面内做简谐振动,O为平衡位置,A,B为最大位移处,当振子由A点从静止开始振动,测得第二次经过平衡位置所用时间为t秒,在O点上方C处有一个小球,现使振子由A点,小球由C点同时从静止释放,它们恰好到O点处相碰,试求小球所在C点的高度H是多少?
[例]如图所示,一弹簧振子在光滑水平面内做简谐振动,O为平衡位置,A,B为最大位移处,当振子由A点从静止开始振动,测得第二次经过平衡位置所用时间为t秒,在O点上方C处有一个小球,现使振子由A点,小球由C点同时从静止释放,它们恰好到O点处相碰,试求小球所在C点的高度H是多少?
解析:由已知振子从A点开始运动,第一次经过O点的时间是1/4周期,第二次经过O点是3/4周期,设其周期T,所以有:t=3T/4,T=4t/3;
振子第一次到O点的时间为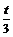 ;振子第二次到点的时间为
;振子第二次到点的时间为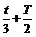 ;振子第三次到O点的时间为
;振子第三次到O点的时间为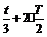 ……第n次到O点的时间为
……第n次到O点的时间为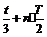 (n=0.1,2,3……)
(n=0.1,2,3……)
C处小球欲与振子相碰,它和振子运动的时间应该是相等的;小球做自由落体运动,所以有
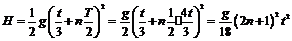
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com