7.(2008·全国Ⅱ理，15)已知F为抛物线C：y²=4x的焦点，过F且斜率为1的直线交抛物线C于A、B两点.设|FA|＞|FB|,则|FA|与|FB|的比值等于　　　　　 .

答案　 3+2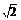

6.设F为抛物线y²=4x的焦点，A、B、C为该抛物线上三点.若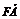++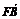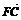=0,则||+||+||=　　　　 .

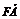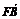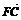答案　 6

5.设坐标原点为O，抛物线y²=2x与过焦点的直线交于A、B两点，则·=　　　　　 .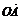

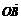答案　 -

4.已知抛物线y²=4x,过焦点的弦AB被焦点分成长为m、n(m≠n)的两段，那么m+n与mn的大小关系是　　　　 .

答案　 相等

3.已知点P是抛物线y²=2x上的动点，点P在y轴上的射影是M，点A的坐标是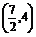，则|PA|+|PM|的最小值是　　　　　 .

答案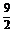　

2.设F为抛物线y²=ax (a＞0)的焦点，点P在抛物线上，且其到y轴的距离与到点F的距离之比为1∶2，则|PF|=　　　 .

答案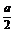　

1.若点P到点F(0，2)的距离比它到直线y+4=0的距离小2，则P的轨迹方程为　　　　　 .

答案　 x²=8y

12. 如图所示的几何体中，四边形AA₁B₁B是边长为3的正方形，CC₁=2，CC₁∥AA₁，这个几何体是棱柱吗？若是，指出是几棱柱.若不是棱柱，请你试用一个平面截去一部分，使剩余部分是一个棱长为2的三棱柱，并指出截去的几何体的特征，在立体图中画出截面.

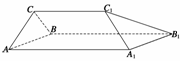
解　 这个几何体不是棱柱；

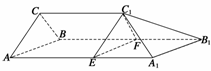
在四边形ABB₁A₁中，在AA₁上取点E，使AE=2；在BB₁上取F使BF=2；连接C₁E，EF，C₁F，则过C₁EF的截面将几何体分成两部分，其中一部分是棱柱ABC-EFC₁，其棱长为2；截去的部分是一个四棱锥C₁-EA₁B₁F.

11.正四棱锥的高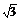为，侧棱长为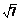，求侧面上斜高(棱锥侧面三角形的高)为多少？

解　 如图所示，正棱锥S-ABCD中高OS=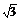，侧棱SA=SB=SC=SD=，

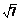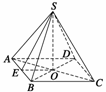在Rt△SOA中，

OA=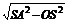=2，

∴AC=4.

∴AB=BC=CD=DA=2.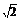

作OE⊥AB于E，则E为AB中点.

连接SE，则SE即为斜高，则SO⊥OE.

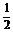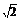在Rt△SOE中，∵OE=BC=，SO=，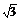

∴SE=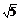，即侧面上的斜高为.

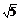10.圆台的一个底面周长是另一个底面周长的3倍，轴截面的面积等于392 cm²,母线与轴的夹角是45°，求这个圆台的高、母线长和两底面半径.

解　 圆台的轴截面如图所示，设圆台上下底面半径分别为x cm,3x cm.延长AA₁交OO₁的延长线于S，

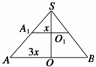在Rt△SOA中，∠ASO=45°,　　　　　　　　　　

则∠SAO=45°，

∴SO=AO=3x，∴OO₁=2x，

又S_轴截面=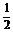(6x+2x)·2x=392，∴x=7.

故圆台的高OO₁=14 (cm)，

母线长l=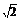O₁O=14 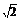(cm)，

两底面半径分别为7 cm,21 cm.