2、抛体的速度

由于运动的等时性，那么大家能否根据前面的结论得到物体做平抛运动的时间？

由y＝1/2gt²得到，运动时间

这说明了什么问题？(这说明了做平抛运动的物体在空中运动的时间仅取决于下落的高度，与初速度无关)

那么落地的水平距离是多大？ (落地的水平距离)

这说明了什么问题？(这说明了平抛运动的水平位移不仅与初速度有关系，还与物体的下落高度有关)利用运动合成的知识，结合图6．4-2，求物体落地速度是多大？结论如何？

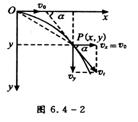
落地速度，即落地速度也只与初速度v和下落高度h有关。平抛运动的速度与水平方向的夹角为a，一般称为平抛运动的偏角。实际上，

常称为平抛运动的偏角公式，在一些问答题中可以直接应用此结论分析解答。

例2：一个物体以l0 m／s的速度从10 m的水平高度抛出，落地时速度与地面的夹角θ是多少(不计空气阻力)？

例3：在5 m高的地方以6 m／s的初速度水平抛出一个质量是10 kg的物体，则物体落地的速度是多大？从抛出点到落地点发生的位移是多大？(忽略空气阻力，取g=10m／s²)

交流与讨论

应用运动的合成与分解的方法我们探究了做平抛运动的物体的位移和速度。请大家根据我们探究的结果研究一下平抛运动的物体位移和速度之间存在什么关系？

1、抛体的位置

我们以平抛运动为例来研究抛体运动所共同具有的性质。

首先我们来研究初速度为v的平抛运动的位置随时间变化的规律。用手把小球水平抛出，小球从离开手的瞬间(此时速度为v，方向水平)开始，做平抛运动，我们以小球离开手的位置为坐标原点，以水平抛出的方向为x轴的方向，竖直向下的方向为y轴的方向，建立坐标系，并从这一瞬间开始计时。

在抛出后的运动过程中，小球受力情况如何？(小球只受重力，重力的方向竖直向下，水平方向不受力。)

那么，小球在水平方向有加速度吗，它将怎样运动？(小球在水平方向没有加速度，水平方向的分速度将保持v不变，做匀速直线运动。)

我们用函数表示小球的水平坐标随时间变化的规律将如何表示？(x=vt)

在竖直方向小球有加速度吗？若有，是多大？它做什么运动？它在竖直方向有初速度吗？

(在竖直方向，根据牛顿第二定律，小球在重力作用下产生加速度g。做自由落体运动，而在竖直方向上的初速度为0)那根据运动学规律，请大家说出小球在竖直方向的坐标随时间变化的规律？(y＝gt²/2)

小球的位置能否用它的坐标(x，y)描述？能否确定小球在任意时刻t的位置？(可以)

那么，小球的运动就可以看成是水平和竖直两个方向上运动的合成。t时间内小球合位移是：

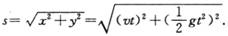
若设s与+x方向(即速度方向)的夹角为θ，如图6．4-1，则其正切值如何求？

例1：一架飞机水平匀速飞行．从飞机上海隔l s释放一个铁球，先后释放4个，若不计空气阻力，从地面上观察4个小球(　　 )

A.在空中任何时刻总是捧成抛物线，它们的落地点是等间距的

B.在空中任何时刻总是排成抛物线，它们的落地点是不等间距的

C.在空中任何时刻总在飞机正下方，排成竖直的直线，它们的落地点是等间距的

D.在空中任何时刻总在飞机的正下方，捧成竖直的直线，它们的落地点是不等间距的。

解析：因为铁球从飞机上释放后做平抛运动，在水平方向上有与飞机相同的速度。不论铁球何时从飞机上释放，铁球与飞机在水平方向上都无相对运动。铁球同时还做自由落体运动，它在竖直方向将离飞机越来越远．所以4个球在落地前始终处于飞机的正下方，并排成一条直线，又因为从飞机上每隔1s释放1个球，而每个球在空中运动的时间又是相等的，所以这4个球落地的时间也依次相差1 s，它们的落地点必然是等间距的．若以飞机为参考系观察4个铁球都做自由落体运动。此题把曲线运动利用分解的方法“化曲为直”，使其成为我们所熟知的直线运动，则据运动的独立性，可以分别在这两个方向上用各自的运动规律研究其运动过程。

22．(本小题满分12分)

已知数列

　 (I)求的通项公式；

　 (II)求证：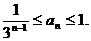

21．(本小题满分12分)

已知A、B是抛物线上的两点，O是抛物线的顶点，OA⊥OB。

　 (I)求证：直线AB过定点M(4，0)；

　 (II)设弦AB的中点为P，求点P到直线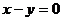的距离的最小值。

20．(本小题满分12分)

　　 已知函数

　 (I)证明：函数；

　 (II)设函数在(-1，1)上单调递增，求a的取值范围。

19．(本小题满分13分)

如图，三棱锥P-ABC中，平面PAC⊥平面BAC，AP=AB=AC=2，∠BAC=∠PAC=120°。

　 (I)求棱PB的长；

　 (II)求二面角P-AB-C的大小。

18．(本小题满分12分)

象棋比赛中，胜一局得2分，负一局得0分，和棋一局得1分，在甲对乙的每局比赛中，甲胜、负、和的概率依次为0.5，0.3，0.2.现此二人进行两局比赛，得分累加。

　 (I)求甲得2分的概率；

　 (II)记甲得分为的分布列和期望。

17．(本小题满分10分)

　　 已知函数

　 (I)求函数的最小正周期；

　 (II)求函数上的最大值与最小值。

16．过点的方程为　　　 。