
4.换元法
例4.求函数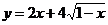 的值域
的值域
解:设 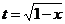 则 t
则 t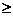 0 x=1-
0 x=1-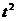
代入得 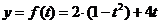
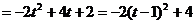
∵t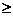 0 ∴y
0 ∴y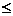 4
4
3.判别式法(△法):
判别式法一般用于分式函数,其分子或分母只能为二次式,解题中要注意二次项系数是否为0的讨论
例3.求函数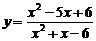 的值域
的值域
方法一:去分母得 (y-1)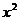 +(y+5)x-6y-6=0 ①
+(y+5)x-6y-6=0 ①
当 y¹1时 ∵xÎR
∴△=(y+5)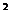 +4(y-1)×6(y+1)
+4(y-1)×6(y+1)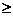 0
0
由此得 (5y+1)
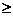 0
0
检验  时
时 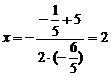 (代入①求根)
(代入①求根)
∵2 Ï 定义域 { x| x¹2且 x¹3} ∴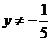
再检验 y=1 代入①求得 x=2 ∴y¹1
综上所述,函数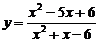 的值域为 { y| y¹1且
y¹
的值域为 { y| y¹1且
y¹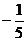 }
}
方法二:把已知函数化为函数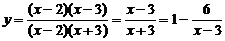 (x¹2)
(x¹2)
由此可得 y¹1 
∵ x=2时  即
即
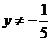
∴函数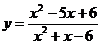 的值域为 { y| y¹1且
y¹
的值域为 { y| y¹1且
y¹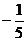 }
}
说明:此法是利用方程思想来处理函数问题,一般称判别式法. 判别式法一般用于分式函数,其分子或分母只能为二次式.解题中要注意二次项系数是否为0的讨论.
2.二次函数比区间上的值域(最值):
例2 求下列函数的最大值、最小值与值域:
①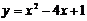 ;
;
②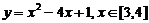 ;
;
③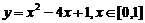 ; ④
; ④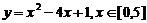 ;
;
解:∵ ,∴顶点为(2,-3),顶点横坐标为2.
,∴顶点为(2,-3),顶点横坐标为2.
①∵抛物线的开口向上,函数的定义域R,
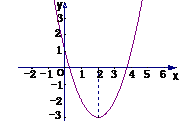 ∴x=2时,ymin=-3 ,无最大值;函数的值域是{y|y
∴x=2时,ymin=-3 ,无最大值;函数的值域是{y|y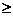 -3 }.
-3 }.
②∵顶点横坐标2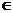 [3,4],
[3,4],
当x=3时,y= -2;x=4时,y=1;
∴在[3,4]上,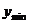 =-2,
=-2,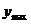 =1;值域为[-2,1].
=1;值域为[-2,1].
③∵顶点横坐标2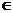 [0,1],当x=0时,y=1;x=1时,y=-2,
[0,1],当x=0时,y=1;x=1时,y=-2,
∴在[0,1]上,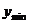 =-2,
=-2,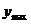 =1;值域为[-2,1].
=1;值域为[-2,1].
④∵顶点横坐标2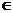 [0,5],当x=0时,y=1;x=2时,y=-3, x=5时,y=6,
[0,5],当x=0时,y=1;x=2时,y=-3, x=5时,y=6,
∴在[0,1]上,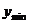 =-3,
=-3,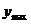 =6;值域为[-3,6].
=6;值域为[-3,6].
注:对于二次函数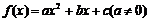 ,
,
⑴若定义域为R时,
①当a>0时,则当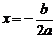 时,其最小值
时,其最小值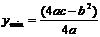 ;
;
②当a<0时,则当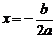 时,其最大值
时,其最大值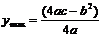 .
.
⑵若定义域为x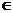 [a,b],则应首先判定其顶点横坐标x0是否属于区间[a,b].
[a,b],则应首先判定其顶点横坐标x0是否属于区间[a,b].
①若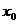
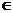 [a,b],则
[a,b],则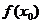 是函数的最小值(a>0)时或最大值(a<0)时,再比较
是函数的最小值(a>0)时或最大值(a<0)时,再比较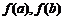 的大小决定函数的最大(小)值.
的大小决定函数的最大(小)值.
②若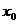
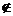 [a,b],则[a,b]是在
[a,b],则[a,b]是在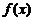 的单调区间内,只需比较
的单调区间内,只需比较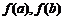 的大小即可决定函数的最大(小)值.
的大小即可决定函数的最大(小)值.
注:①若给定区间不是闭区间,则可能得不到最大(小)值;
②当顶点横坐标是字母时,则应根据其对应区间特别是区间两端点的位置关系进行讨论.
1.直接法:利用常见函数的值域来求
一次函数y=ax+b(a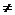 0)的定义域为R,值域为R;
0)的定义域为R,值域为R;
反比例函数 的定义域为{x|x
的定义域为{x|x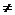 0},值域为{y|y
0},值域为{y|y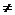 0};
0};
二次函数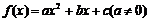 的定义域为R,
的定义域为R,
当a>0时,值域为{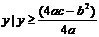 };当a<0时,值域为{
};当a<0时,值域为{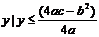 }.
}.
例1.求下列函数的值域
① y=3x+2(-1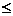 x
x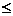 1) ②
1) ②
③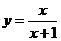 ④
④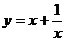

解:①∵-1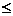 x
x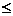 1,∴-3
1,∴-3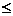 3x
3x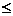 3,
3,
∴-1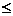 3x+2
3x+2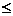 5,即-1
5,即-1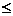 y
y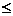 5,∴值域是[-1,5]
5,∴值域是[-1,5]
②∵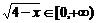 ∴
∴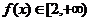

即函数 的值域是 { y| y
的值域是 { y| y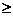 2}
2}
③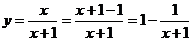
∵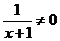 ∴
∴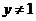
即函数的值域是 { y| yÎR且y¹1}(此法亦称分离常数法)
④当x>0,∴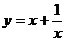 =
=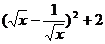
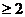 ,
,
当x<0时,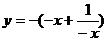 =-
=-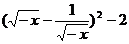
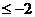

∴值域是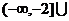 [2,+
[2,+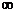 ).(此法也称为配方法)
).(此法也称为配方法)
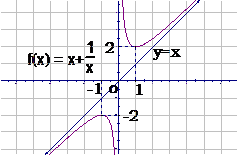 函数
函数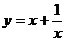 的图像为:
的图像为:
函数的三要素是:定义域、值域和定义域到值域的对应法则;对应法则是函数的核心(它规定了x和y之间的某种关系),定义域是函数的重要组成部分(对应法则相同而定义域不同的映射就是两个不同的函数);定义域和对应法则一经确定,值域就随之确定
函数的表示方法⑴解析法优点:一是简明、全面地概括了变量间的关系;二是可以通过解析式求出任意一个自变量的值所对应的函数值.中学阶段研究的函数主要是用解析法表示的函数.
⑵列表法优点:不需要计算就可以直接看出与自变量的值相对应的函数值.
⑶图象法:优点:能直观形象地表示出自变量的变化,相应的函数值变化的趋势,这样使得我们可以通过图象来研究函数的某些性质.
前面我们已经学习了函数定义域的求法和函数的表示法,今天我们来学习求函数值域的几种常见方法
|
|
化合反应 |
分解反应 |
置换反应 |
复分解反应 |
|
定义 |
|
|
|
|
|
形式 |
|
|
|
|
|
举例 |
|
|
|
|
思考:画出反映四种基本反应类型与氧化还原反应的关系图。
试题枚举
[例1]古诗词是古人为我们留下的宝贵的精神财富。下列诗句只涉及物理变化的是()。
A. 野火烧不尽,春风吹又生
B. 春蚕到死丝方尽,蜡炬成灰泪始干
C. 只要功夫深,铁杵磨成针
D. 爆竹声中一岁除,春风送暖入屠苏
解析:选项A、B、D均涉及有关燃烧的知识,属于化学变化;“铁杵磨成针”只是发生了形变,属于物理变化。
答案:C
[例2]关于化学反应A+B=C+D下列说法中正确的是( )。
A.若生成物C和D分别是盐和水,则反应物一定是酸和碱
B.若A和C是单质,B和D是化合物,则该反应一定是置换反应
C.若A是可溶性碱,B是可溶性盐,则C和D可能是两种沉淀
D.若A、B各取10g混合,使其充分反应,则C、D质量的总和一定等于20g
解析:对一个概念作出判断应弄清它的含义,把握它的实质。B、C符合概念和反应规律,正确。A中由于生成盐和水的反应可以在多种物质类别间发生,如:碱和酸性氧化物,酸和碱性氧化物之间也都能生成盐和水。D中A、B各10g物质可能恰好反应完,也可能其中一种没有反应完,则生成物的总和应≤20g。
答案:B、C。
[例3]下列过程不涉及化学变化的是( )
A.甘油加水作护肤剂
B.用明矾净化水
C.烹鱼时加入少量的料酒和食醋可减少腥味,增加香味
D.烧菜用过的铁锅,经放置常出现红棕色斑迹
解析:化学变化与物理变化的本质区别是:是否有新物质生成。甘油稀释后仍具有吸湿性,可做护肤品,该过程不涉及化学变化。
明矾溶于水后,发生反应:Al3+ + 3H2O 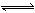 Al(OH)3 + 3H+ 产生氢氧化铝胶体,从而可净化水。
Al(OH)3 + 3H+ 产生氢氧化铝胶体,从而可净化水。
烹鱼时加入少量的料酒和食醋可减少腥味,增加香味的原因是过程中发生了 CH3COOH + C2H5OH →CH3COOC2H5+ H2O ,产生了具有香味的乙酸乙酯的缘故。
烧菜用过的铁锅,由于在潮湿的环境中发生了电化腐蚀,Fe最终被氧化成Fe2O3•nH2O而出现红棕色斑迹,后三者都是化学变化过程。
答案:A
5. 从有无离子参加分为:
4. 根据反应程度分为
3. 从热效应分为:
2. 从有无电子转移分为:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com