
1. 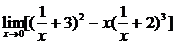
解: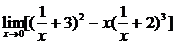
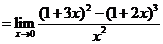
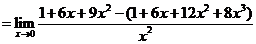
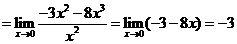
∴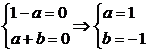
解:(2)
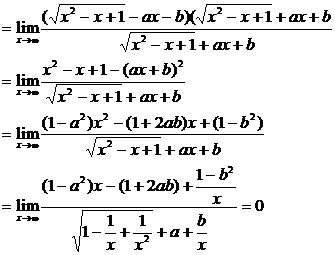
要使极限存在1-a2=0.
∴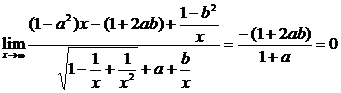
即1+2ab=0,a+1≠0.
∴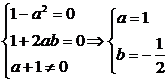
解:(3)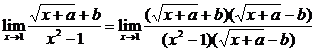
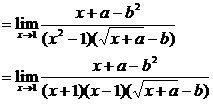
当x→1时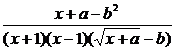 极限存在,则分子、分母必有公因式x-1. ∴a-b2=-1
极限存在,则分子、分母必有公因式x-1. ∴a-b2=-1
∴原式=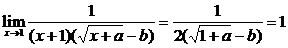
∴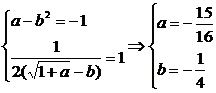
说明:第一题是分子分母同除以x的较低的幂,第二题是分子有理化,和第一题的方法相结合,第三题是因式分解法和分子有理化法相结合.
我们以前求极限的一种方法是分子、分母同除x的最高次幂,但像第一题,因为分子的次数低于分母的次数,如果分子除以x2,则分子极限为0,不符合,所以通分后,应除以分子分母中x的较低次幂.并且x的次数比分子x的最高次幂大的项的系数应该等于0,这样极限才存在.
例3 f(x)=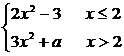 求a,使
求a,使 f(x)存在.
f(x)存在.
解:要使 f(x)存在,则
f(x)存在,则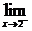 f(x)与
f(x)与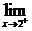 f(x)要存在且相等.
f(x)要存在且相等.
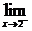 f(x)=
f(x)= 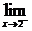 (2x2-3)=2·22-3=5.
(2x2-3)=2·22-3=5.
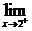 f(x)=
f(x)= 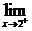 (3x2+a)=3·22+a=12+a.
(3x2+a)=3·22+a=12+a.
∴5=12+a.∴a=-7
例4设函数f(x)=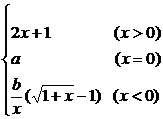 ,在x=0处连续,求a,b的值.
,在x=0处连续,求a,b的值.
分析:要使f(x)在x=0处连续,就要使f(x)在x=0处的左、右极限存在,并且相等,等于f(x)在x=0处的值a.
解: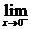 f(x)=
f(x)=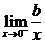 ·(
·(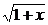 -1)
-1)

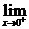 f(x)=
f(x)=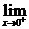 (2x+1)=2·0+1=1
(2x+1)=2·0+1=1
∴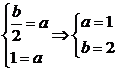
说明:这类连续的题目,也关键是求在一点处的左、右极限存在并都等于在这点的函数值,与函数在这点的极限存在的方法是相同的

例1 已知数列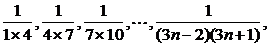 …
…
(1)计算S1,S2,S3,S4.
(2)猜想Sn的表达式,并证明.
(3)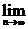 Sn.
Sn.
解:(1)S1=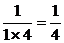 .
.
S2=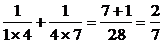
S3=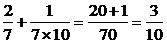
S4=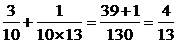 .
.
(2 )解:通项是以3n-2,3n+1两数乘积为分母的,而我们看到,在表示上面四个结果的分数中,分子可用项数n表示,分母可用3n+1表示,于是可猜想.
Sn=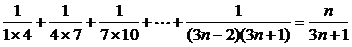
证明方法一:用数学归纳法证明如下:
1° 当n=1时,S1=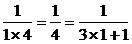 等式成立.
等式成立.
2° 假设当n=k时等式成立.即 Sk=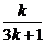 .
.
当n=k+1时.
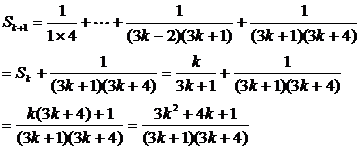
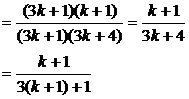
∴当n=k+1时,等式也成立.
∴Sn=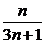 (n∈N*)
(n∈N*)
证明方法二: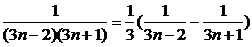
∴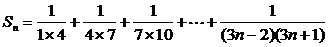
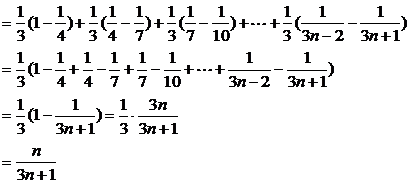
∴Sn=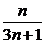
(3)解: 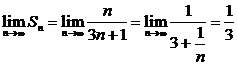
例2 已知下列极限,求a与b.
(1)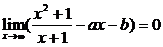
(2)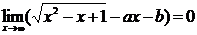
(3)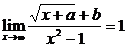
分析:此题属于已知x趋向于x0(或无穷大)时,函数的极限存在且等于某个常数,求函数关系式的类型.上边三个小题都不能简单地将x=x0直接代入函数的解析式中,因为(1)(2)中的x不趋于确定的常数,(3)虽然趋于1,但将x=1代入函数关系式中,分母为零.因此,解决此类问题的关键,是先要确定用哪种方法求极限,再将函数的解析式进行适当的变形,然后根据所给的条件进行分析,进而确定a,b的值.
解:(1)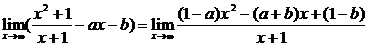
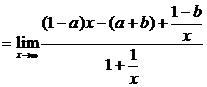
1° 如果1-a≠0,
∵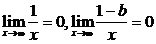
∴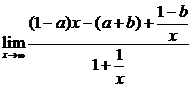 不存在.
不存在.
2° 如果 1-a=0,
∵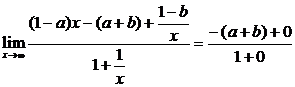
(8) 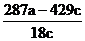 或
或
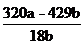
16、(2010·长春模拟)下图是部分常见元素的单质及其化合物的转化关系图(有关反应条件及生成的部分产物已略去)。
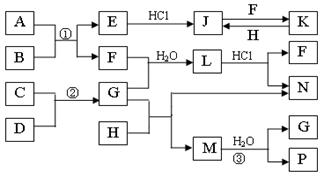
已知:A为硫铁矿的主要成分,E为红棕色固体,K为浅绿色溶液;反应①、②都是化工生产中的重要反应;B、C、D、H是单质;B、C、D、F、G、H常温下是气态; F、P 和H的水溶液均具有漂白作用,且F是形成酸雨的主要物质之一;N是一种常见的氮肥;化合物G分子构型为三角锥形,化合物M由两种元素组成,分子内共有58个电子。
(1)F的化学式 ;G的水溶液中,最多的阳离子是 。
(2)写出K与H反应的离子方程式: ;
G与H反应的化学方程式: 。
(3)在实验室中,向饱和H水溶液中加入CaCO3粉末,充分反应后过滤,可制得浓度较大的P的水溶液。用化学平衡移动的原理加以解释
[答案](1)SO2 、NH4+
(2)2Fe2+ + Cl2 = 2Fe3+ + 2Cl- 4NH3 + 3Cl2 = NCl3 + 3NH4Cl
(3)饱和的Cl2水中存在如下平衡:Cl2 + H2O  H+ + Cl- + HClO ,加入的CaCO3
H+ + Cl- + HClO ,加入的CaCO3
粉末与H+ 反应,使上述平衡向正向移动,HClO浓度增大
()
例1如图,已知正方形ABCD的边长为4,E、F分别是AB、AD的中点,GC⊥平面ABCD,且GC=2,求点B到平面EFG的距离.
分析:由题设可知CG、CB、CD两两互相垂直,可以由此建立空间直角坐标系.用向量法求解,就是求出过B且垂直于平面EFG的向量,它的长即为点B到平面EFG的距离.
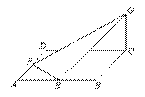 解:如图,设
解:如图,设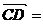 4i,
4i,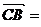 4j,
4j,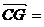 2k,
2k,
以i、j、k为坐标向量建立空间直角坐标系C-xyz.
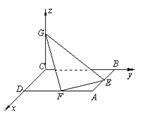 由题设C(0,0,0),A(4,4,0),B(0,4,0),D(4,0,0),E(2,4,0),F(4,2,0),G(0,0,2).
由题设C(0,0,0),A(4,4,0),B(0,4,0),D(4,0,0),E(2,4,0),F(4,2,0),G(0,0,2).
∴ 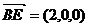 ,
,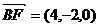 ,
,
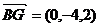 ,
, ,
,
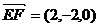 .
.
设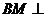 平面EFG,M为垂足,则M、G、E、F四点共面,由共面向量定理知,存在实数a、b、c,使得
平面EFG,M为垂足,则M、G、E、F四点共面,由共面向量定理知,存在实数a、b、c,使得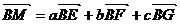
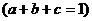 ,
,
∴ 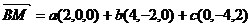 =(2a+4b,-2b-4c,2c).
=(2a+4b,-2b-4c,2c).
由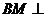 平面EFG,得
平面EFG,得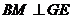 ,
,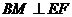 ,于是
,于是
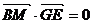 ,
,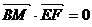 .
.
∴ 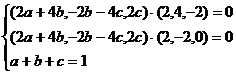
整理得: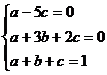 ,解得
,解得 .
.
∴ 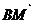 =(2a+4b,-2b-4c,2c)=
=(2a+4b,-2b-4c,2c)= .
.
∴ 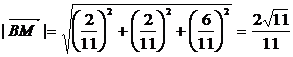
故点B到平面EFG的距离为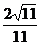 .
.
说明:用向量法求点到平面的距离,常常不必作出垂线段,只需利用垂足在平面内、共面向量定理、两个向量垂直的充要条件解出垂线段对应的向量就可以了.
例2 已知正方体ABCD-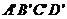 的棱长为1,求直线
的棱长为1,求直线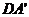 与AC的距离.
与AC的距离.
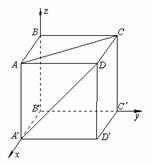 分析:设异面直线
分析:设异面直线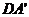 、AC的公垂线是直线l,则线段
、AC的公垂线是直线l,则线段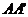 在直线l上的射影就是两异面直线的公垂线段,所以此题可以利用向量的数量积的几何意义求解.
在直线l上的射影就是两异面直线的公垂线段,所以此题可以利用向量的数量积的几何意义求解.
解:如图,设 i,
i,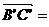 j,
j,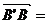 k,以i、j、k为坐标向量建立空间直角坐标系
k,以i、j、k为坐标向量建立空间直角坐标系 -xyz,
-xyz,
则有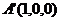 ,
,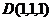 ,
,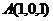 ,
,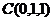 .
.
∴ 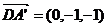 ,
,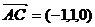 ,
,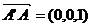 .
.
设n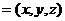 是直线l方向上的单位向量,则
是直线l方向上的单位向量,则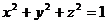 .
.
∵ n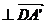 ,n
,n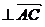 ,
,
∴ 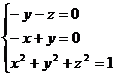 ,解得
,解得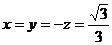 或
或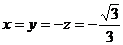 .
.
取n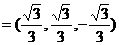 ,则向量
,则向量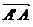 在直线l上的投影为
在直线l上的投影为
n·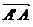
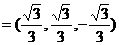 ·
·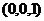
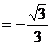 .
.
由两个向量的数量积的几何意义知,直线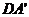 与AC的距离为
与AC的距离为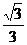 .
.
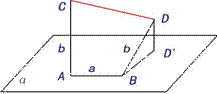 例3 如图,已知线段AB在平面α内,线段
例3 如图,已知线段AB在平面α内,线段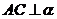 ,线段BD⊥AB,线段
,线段BD⊥AB,线段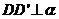 ,
,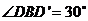 ,如果AB=a,AC=BD=b,求C、D间的距离.
,如果AB=a,AC=BD=b,求C、D间的距离.
解:由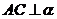 ,可知
,可知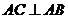 .
.
由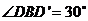 可知,<
可知,<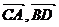 >=
>=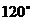 ,
,
∴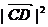 =
=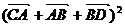
=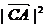 +
+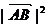 +
+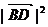 +2(
+2( +
+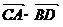 +
+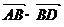 )
)
=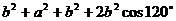 =
=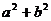 .
.
∴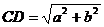 .
.
小结:选定空间同起点且不公面的三个向量作为一个基底,并用它表示指定的向量,是用向量知识解决立体几何问题的基本要领.解题中要结合已知和未知去观察图形、联想有关的运算法则和公式等,就近表示所需的向量,再对照目标将不符合要求的向量加以调整,如此反复,直至所有向量符合目标要求.
例4.如果一条直线与一个平面平行那麽过这个平面内的一点与这条直线平行的直线必在这个平面内
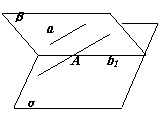 已知:a∥α,AÎa,AÎb且a∥b
已知:a∥α,AÎa,AÎb且a∥b
求证:bÌa
证明:假设bËa过A点和a确定平面为b,
b∩a=b1,b1Ìa,AÎb1
∵a∥α ∴a∥b1
由a∥b而b,b1都过点A
这样,在平面a内过A有两条直线b和b1都平行于a
这是不可能的 ∴bÌa
∴bÌa
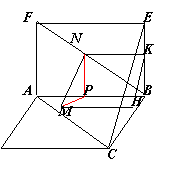
例5.正方形ABCD和正方形ABEF所在平面互相垂直,点M,N分别在对角线AC和BF上,且AM=FN
求证:MN∥平面BEC
分析:证线面平行Ü线线平行,需找出面BEC中与MN平行的直线
证法(一):作NK∥AB交BE于K,作MH∥AB交BC于H
∴MH∥NK
∵ABCD与ABEF是两个有公共边AB的正方形
 ∴它们是全等正方形
∴它们是全等正方形
∵AM=FN ∴CM=BN
又∠HCM=∠KBN,∠HMC=∠KNB
∴△HCM≌△KBN ∴MH=NK
∴MHKN是平行四边形 ∴MN∥HK
∵HKÌ平面BEC MNË平面BEC
∴MN∥平面BEC
证法(二):分析:利用面面平行Þ线面平行
过N作NP∥BE,连MP,∵NP∥AF
∴FN/FB=AP/AB ∴AM=FN,AC=BF
∴FN/FB=AM/AC ∴AP/AB=AM/AC
∴MP∥BC ∴平面MNP∥平面BCE
∴MN∥平面BCE
例6.在三棱锥P-ABC中,三条侧棱PA,PB,PC两两垂直,H是△ABC的垂心
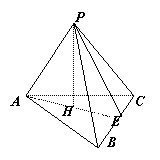 求证:⑴PH^底面ABC ⑵△ABC是锐角三角形
求证:⑴PH^底面ABC ⑵△ABC是锐角三角形
证明:⑴∵PA^PB PA^PC且PB∩PC=P
∴PA^侧面PBC 又∵BCÌ平面PBD ∴PA^BC
∵H是△ABC的垂心 ∴AH^BC
∵PA∩AH=A ∴BC^截面PAH
又PHÌ平面PAH ∴BC^PH
同理可证:AB^PH 又ABÇBC=B ∴PH^面ABC
⑵设AH与直线BC的交点为E,连接PE
由⑴知PH^底面ABC ∴AE为PE在平面ABC的射影
由三垂线定理:PE^BC
∵PB^PC即△BPC是直角三角形,BC为斜边
∴E在BC边上 由于AE^BC,故B∠C都是锐角
同理可证:∠A也是锐角 ∴△ABC为锐角三角形
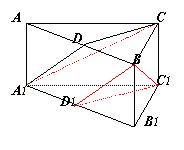
例7.正三棱柱ABC-A1B1C1的侧面三条对角线AB1,BC1,CA1中,AB1^BC1
求证:AB1^CA1
证明:取AB,A1B1中点D,D1连接CD,C1D1及A1D,BD1
 由三棱柱可知,面A1B1C1^面AB1
由三棱柱可知,面A1B1C1^面AB1
在正△A1B1C1中,C1D1^A1B1
∴C1D1^面AB1 (同理CD^面AB1)
∴BD1是BC1在平面AB1内的射影
∵AB1^BC1 ∴AB1^BD1 ∵BD1∥AD1 ∴AB1^A1D
且AD1是A1C在平面AB1内的射影 ∴AB1^A1C
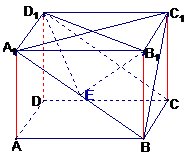
例8.在正四棱柱AC1中,底面边长为1,侧棱长为2,
⑴求D1B1与平面A1BCD1所成的角
⑵求B1到平面A1BC1的距离
分析:⑴按定义需作B1D1在平面A1BCD1上的射影,那麽在此平面上射影的位置该落何处,这就是要考虑垂足的定位问题
常用方法:⑴ 过B1作A1B的垂线B1EÞB1E^平面A1BCD1
⑵ 过B1作平面A1BCD1的垂线ÞB1EÌ平面A1BCD1ÞEÎA1B
 (3) 在垂面内做垂线
(3) 在垂面内做垂线
解:⑴ BC^AB , BC^BB1 ∴BC^面A1B∴面A1C^面A1B
过B1作B1E^A1B=E ∴B1E^平面A1BCD1
连D1E,则D1E是B1D1在平面A1BCD1上的射影
故∠ B1D1E即B1D1与平面A1BCD1所成的角
且在Rt△ B1ED1中,B1E=A1B1*B1B/A1B=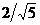
∴Sin∠ B1D1E=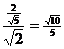
(2)解一:正方形A1B1C1D1中 , 等腰ΔBA1C1中A1C1^ B1D1 ,BO^ A1C1
∴A1C1^面B1BO ∴面A1C1B^面B1BO
∴过B1作高线BO垂线 B1 H^ BO于H 则B1 H^面A1C1B
连A1C1,过B1作平面A1BC1的垂线,垂足为H,则B1H的长
即点B1到平面A1BC1的距离,
由正棱柱性质:B1A1,B1C1,B1B两两垂直∴H是△A1BC1的垂心
连BO则BO^A1C1 ∴HÎBO
∵B1B^底面A1C1 ∴B1B^B1O,B1H^BO
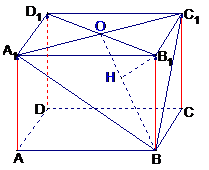 B1H=
B1H=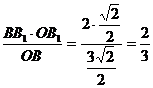
(OB=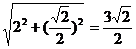 )
)
即顶点B1到截面A1BC1的距离为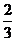

解二:(利用等积法)考察四面体B1A1BC1
设顶点B1到A1BC1的距离为h
则为三棱柱B1-A1BC1的高
VB1-A1BC1=VB-ABC1
∴ *S△A1BC1*h=
*S△A1BC1*h= *S△A1BC1*B1B ∵A1C1^BO
*S△A1BC1*B1B ∵A1C1^BO
∴ *
*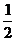 *A1C1*BO*h=
*A1C1*BO*h= *
*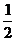 *A1B1*B1C1*BB1
*A1B1*B1C1*BB1
∴B到平面A1BC1的距离为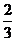

(三)卤素单质的化学性质(相似性及递变性)
由于最外层均为 个电子,极易 电子,因此卤素都是 剂,在自然界均只以 态存在.但随着电子层数递增,原子半径渐 ,核对外层电子的引力渐 ,得电子能力渐 ,其氧化性逐渐 ,主要表现:
。
试题枚举
[例1]下列有关氯的叙述中正确的是
A.液氯和氯水是同一物质
B.红磷在氯气中燃烧产生白色烟雾
C.氯气与水的反应中氯是氧化剂,水是还原剂
D.用氯制漂白粉是为了得到易贮存的漂白剂
解析:液氯、氯水都是液体,但前者是纯氯,后者是氯与水的混合物,时间延长氯水中还逐渐生成盐酸和次氯酸,氯分子渐少,氯离子渐多。如果再有光照, 因分解也在渐少,出现氧气和更多盐酸。氯与水的反应是氯分子中氯原子间发生的自身氧化还原,即歧化反应, 水虽然是反应物,却未参加氧化还原。A、C不正确。
烟是分散在气体中的固体小颗粒,雾是分散在气体里的液体小珠滴。磷在氯气里燃烧的产物三氯化磷是无色液体,可发雾;五氯化磷是浅黄色固体,能形成烟。漂白粉和氯都可以作为漂白剂、消毒剂,且氯更有效。但氯气难贮存,又有剧毒,一般医用、家用的漂白剂和消毒剂使氯气是不合宜的,所以制成漂白粉便于贮存和使用。漂白粉保存得当,如密闭,以防止吸水和 而变质,可以存放较长时间。B、D正确。
答案:B、D。
[例2] 潮湿的氯气、新制的氯水、次氯酸钠及漂白粉的水溶液均能使有色布条褪色,原因是它们均含有 ( )
A. 氯气 B. 次氯酸 C. 次氯酸根 D. 氯化氢
解析 NaClO及Ca(ClO)2的水溶液中,ClO-水解产生HClO无HCl;有色布条的褪色是因HClO的氧化所致。
答案: B
[变式] 用滴管将新制的氯水慢慢滴入盛酚酞的氢氧化钠稀溶液中,当滴到最后一滴时红色突然褪去,发生这一现象的原因可能有两个:
①是由于 (用简要文字说明)
②是由于 (用简要文字说明)
简述用实验方法证明褪色的原因是①还是②
。
[例3]如何鉴别NaCl、NaBr、KI三种白色固体?
解答:
方法一:可用氯水鉴别。
把这三种物质各取少量制成溶液,加入新制的氯水和汽油(或四氯化碳),振荡,分层,使汽油层呈无色的是NaCl;使汽油层呈橙色的是NaBr;呈紫色的是KI。
方法二:可先用焰色反应将KI区分出来。然后再将另外两种物质各取少量制成溶液,加入AgNO3溶液,有白色沉淀生成的是NaCl,有浅黄色沉淀生成的是NaBr。
方法三:直接加入AgNO3溶液。
分别取少量固体制成溶液,分别加入AgNO3溶液,有白色沉淀生成的是NaCl,有浅黄色沉淀生成的是NaBr,有黄色沉淀生成的是KI。
[例4] 多原子分子氰(CN)2、硫氰(SCN)2和(OCN)2的性质与卤素单质相似,故称它们为拟卤素。它们可以生成酸和盐(见下表,表中X代表F、Cl、Br或I)。
|
|
卤素 |
氰 |
硫氰 |
① |
|
“单质” |
X2 |
(CN)2 |
(SCN)2 |
(OCN)2 |
|
酸 |
HX |
HCN |
② |
HOCN |
|
盐 |
KX |
KCN |
KSCN |
③ |
(1)在表中①②③空格处应分别填写_______、_______、_______。
(2)完成下列反应的化学方程式或离子方程式。
①(CN)2和KOH溶液反应的化学方程式为:______________。
②已知阴离子的还原性强弱为:Cl-<Br-<CN-<SCN-<I-。试写出在NaBr和KSCN的混合溶液中加入(CN)2反应的离子方程式:____________________________________。
解析:此题主要考查“运用已学知识进行类推思维的能力”。解题时可用熟知的Cl2、HCl、KCl等物质作参照物。由还原性Br-<CN-<SCN-,可推知氧化性Br2>(CN)2>(SCN)2,因而可判断(CN)2只能与KSCN反应,不能与NaBr反应,亦即由物质的氧化性和还原性的强弱,可以判断氧化还原反应能否发生。
答案:(1)氧氰 HSCN KOCN
(2)①(CN)2+2KOH====KCN+KOCN+H2O
②(CN)2+2SCN-====2CN-+(SCN)2
该题为信息给予题,给予的信息是:拟卤素(如(CN)2)的性质与卤素单质相似,由此而可依据卤素单质的性质来进行类比、模拟来解答习题。这是解答信息给予题的一种方法。
[变式] 溴化碘(IBr)的化学性质与卤素单质相似,能与大多数金属反应生成金属卤化物,和某些非金属单质反应生成相应的卤化物,跟水反应的方程式IBr+H2O=HBr+HIO,下列有关IBr的叙述中,不正确的是 ( )
A. IBr是双原子分子
B.在很多反应中IBr是强氧化剂
C.和NaOH溶液反应生成NaBr和NaIO
D.和水反应时,既是氧化剂又是还原剂
 [例5]在右图的四条直线分别表示钠、镁、铝、铁与足量Cl2反应时,消耗金属的质量(纵轴)与反应掉的氯气质量(横轴)的关系,其中代表铁与Cl2反应的直线是
( )
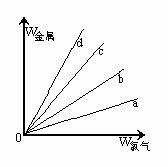
[例5]在右图的四条直线分别表示钠、镁、铝、铁与足量Cl2反应时,消耗金属的质量(纵轴)与反应掉的氯气质量(横轴)的关系,其中代表铁与Cl2反应的直线是
( )
A. a B. b C. c D. d
解析 Cl2与四种金属反应的均为氧化还原反应,在横坐标上取一点作一条垂直于横坐标的直线,分别与a、b、c、d四条直线的交点即为四种金属与等质量Cl2反应时所需的质量。假设这一点的质量为35.5g,此时金属均转移1mol电子,则消耗四种金属的质量分别为:WNa=23g、WMg=12g、WAl=9g、WFe=18.7g,即等质量氯气消耗四种金属的质量是WNa>WFe>WMg>WAl,故a、b、c、d分别代表Al、Mg、Fe、Na与氯气的反应。
答案:C
(二)单质的物理性质
随卤素核电荷数增加,其原子结构的递变而使卤素单质的物理性质呈规律性变化.
归纳:从F2 →I2
1、颜色逐渐 ,状态从 → → ,密度从 → ,熔沸点由 → (原因是 。
2、单质的溶解性--除氟外(与水剧烈反应)在水中溶解度都较 ,且由 → ,都易溶于有机溶剂,下表列出Cl2、Br2、I2在不同溶剂中的颜色.
|
|
水 |
CCl4 |
|
|
Cl2 |
|
|
|
|
Br2 |
|
|
|
|
I2 |
|
|
|
(一)卤素的原子结构
共同点:原子的最外层均为 个电子,都易 1个电子而表现 性;
不同点:核电荷数逐渐 ;电子层数逐渐 ;原子半径依次 ,得电子能力逐渐 ;单质氧化性逐渐 。
2、原理:被检液中滴入少量 酸化,再滴入 溶液,若产生 ,则可断定溶液中含有氯离子。不可用盐酸酸化,酸化目的是防止( 、 、 、 )影响。
+ AgNO3(aq) → + 稀硝酸 →白色↓
解释:Ag+ + Cl- = AgCl↓
2Ag+ + 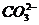 = Ag2CO3↓ Ag2CO3 + 2H+ = 2Ag+ + H2O + CO2↑
= Ag2CO3↓ Ag2CO3 + 2H+ = 2Ag+ + H2O + CO2↑
1、填写下列表格:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com