
3.最值
(1)定义:
最大值:一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:①对于任意的x∈I,都有f(x)≤M;②存在x0∈I,使得f(x0) = M。那么,称M是函数y=f(x)的最大值。
最小值:一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:①对于任意的x∈I,都有f(x)≥M;②存在x0∈I,使得f(x0) = M。那么,称M是函数y=f(x)的最大值。
注意:
1 函数最大(小)首先应该是某一个函数值,即存在x0∈I,使得f(x0) = M;
2 函数最大(小)应该是所有函数值中最大(小)的,即对于任意的x∈I,都有f(x)≤M(f(x)≥M)。
(2)利用函数单调性的判断函数的最大(小)值的方法:
1 利用二次函数的性质(配方法)求函数的最大(小)值;
2 利用图象求函数的最大(小)值;
3 利用函数单调性的判断函数的最大(小)值:
如果函数y=f(x)在区间[a,b]上单调递增,在区间[b,c]上单调递减则函数y=f(x)在x=b处有最大值f(b);
如果函数y=f(x)在区间[a,b]上单调递减,在区间[b,c]上单调递增则函数y=f(x)在x=b处有最小值f(b);
2.单调性
(1)定义:一般地,设函数y=f(x)的定义域为I, 如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x1<x2时,都有f(x1)<f(x2)(f(x1)>f(x2)),那么就说f(x)在区间D上是增函数(减函数);
注意:
1 函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;
2 必须是对于区间D内的任意两个自变量x1,x2;当x1<x2时,总有f(x1)<f(x2)
(2)如果函数y=f(x)在某个区间上是增函数或是减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间。
(3)设复合函数y= f[g(x)],其中u=g(x) , A是y= f[g(x)]定义域的某个区间,B是映射g : x→u=g(x) 的象集:
①若u=g(x) 在 A上是增(或减)函数,y= f(u)在B上也是增(或减)函数,则函数y= f[g(x)]在A上是增函数;
②若u=g(x)在A上是增(或减)函数,而y= f(u)在B上是减(或增)函数,则函数y= f[g(x)]在A上是减函数。
(4)判断函数单调性的方法步骤
利用定义证明函数f(x)在给定的区间D上的单调性的一般步骤:
1 任取x1,x2∈D,且x1<x2;
2 作差f(x1)-f(x2);
3 变形(通常是因式分解和配方);
4 定号(即判断差f(x1)-f(x2)的正负);
5 下结论(即指出函数f(x)在给定的区间D上的单调性)。
(5)简单性质
①奇函数在其对称区间上的单调性相同;
②偶函数在其对称区间上的单调性相反;
③在公共定义域内:
增函数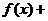 增函数
增函数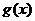 是增函数;
是增函数;
减函数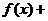 减函数
减函数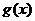 是减函数;
是减函数;
增函数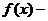 减函数
减函数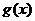 是增函数;
是增函数;
减函数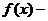 增函数
增函数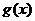 是减函数。
是减函数。
1.奇偶性
(1)定义:如果对于函数f(x)定义域内的任意x都有f(-x)=-f(x),则称f(x)为奇函数;如果对于函数f(x)定义域内的任意x都有f(-x)=f(x),则称f(x)为偶函数。
如果函数f(x)不具有上述性质,则f(x)不具有奇偶性.如果函数同时具有上述两条性质,则f(x)既是奇函数,又是偶函数。
注意:
1 函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;
2 由函数的奇偶性定义可知,函数具有奇偶性的一个必要条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量(即定义域关于原点对称)。
(2)利用定义判断函数奇偶性的格式步骤:
1 首先确定函数的定义域,并判断其定义域是否关于原点对称;
2 确定f(-x)与f(x)的关系;
3 作出相应结论:
若f(-x) = f(x) 或 f(-x)-f(x) = 0,则f(x)是偶函数;
若f(-x) =-f(x) 或 f(-x)+f(x) = 0,则f(x)是奇函数。
(3)简单性质:
①图象的对称性质:一个函数是奇函数的充要条件是它的图象关于原点对称;一个函数是偶函数的充要条件是它的图象关于y轴对称;
②设 ,
,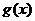 的定义域分别是
的定义域分别是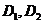 ,那么在它们的公共定义域上:
,那么在它们的公共定义域上:
奇+奇=奇,奇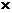 奇=偶,偶+偶=偶,偶
奇=偶,偶+偶=偶,偶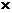 偶=偶,奇
偶=偶,奇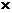 偶=奇
偶=奇
从近几年来看,函数性质是高考命题的主线索,不论是何种函数,必须与函数性质相关联,因此在复习中,针对不同的函数类别及综合情况,归纳出一定的复习线索。
预测2007年高考的出题思路是:通过研究函数的定义域、值域,进而研究函数的单调性、奇偶性以及最值。
预测明年的对本讲的考察是:
(1)考察函数性质的选择题1个或1个填空题,还可能结合导数出研究函数性质的大题;
(2)以中等难度、题型新颖的试题综合考察函数的性质,以组合形式、一题多角度考察函数性质预计成为新的热点。
2.结合具体函数,了解奇偶性的含义;
1.通过已学过的函数特别是二次函数,理解函数的单调性、最大(小)值及其几何意义;
3.求函数值域的各种方法
函数的值域是由其对应法则和定义域共同决定的。其类型依解析式的特点分可分三类:(1)求常见函数值域;(2)求由常见函数复合而成的函数的值域;(3)求由常见函数作某些“运算”而得函数的值域。
①直接法:利用常见函数的值域来求
一次函数y=ax+b(a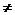 0)的定义域为R,值域为R;
0)的定义域为R,值域为R;
反比例函数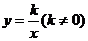 的定义域为{x|x
的定义域为{x|x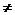 0},值域为{y|y
0},值域为{y|y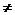 0};
0};
二次函数 的定义域为R,
的定义域为R,
当a>0时,值域为{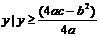 };
};
当a<0时,值域为{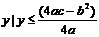 }。
}。
②配方法:转化为二次函数,利用二次函数的特征来求值;常转化为型如: 的形式;
的形式;
③分式转化法(或改为“分离常数法”)
④换元法:通过变量代换转化为能求值域的函数,化归思想;
⑤三角有界法:转化为只含正弦、余弦的函数,运用三角函数有界性来求值域;
⑥基本不等式法:转化成型如: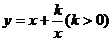 ,利用平均值不等式公式来求值域;
,利用平均值不等式公式来求值域;
⑦单调性法:函数为单调函数,可根据函数的单调性求值域。
⑧数形结合:根据函数的几何图形,利用数型结合的方法来求值域。
2.求函数定义域一般有三类问题:
(1)给出函数解析式的:函数的定义域是使解析式有意义的自变量的取值集合;
(2)实际问题:函数的定义域的求解除要考虑解析式有意义外,还应考虑使实际问题有意义;
(3)已知 的定义域求
的定义域求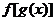 的定义域或已知
的定义域或已知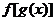 的定义域求
的定义域求 的定义域:
的定义域:
①掌握基本初等函数(尤其是分式函数、无理函数、对数函数、三角函数)的定义域;
②若已知 的定义域
的定义域 ,其复合函数
,其复合函数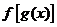 的定义域应由
的定义域应由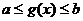 解出。
解出。
“函数”是数学中最重要的概念之一,学习函数的概念首先要掌握函数三要素的基本内容与方法。由给定函数解析式求其定义域这类问题的代表,实际上是求使给定式有意义的x的取值范围 它依赖于对各种式的认识与解不等式技能的熟练。
它依赖于对各种式的认识与解不等式技能的熟练。
1.求函数解析式的题型有:
(1)已知函数类型,求函数的解析式:待定系数法;
(2)已知 求
求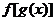 或已知
或已知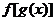 求
求 :换元法、配凑法;
:换元法、配凑法;
(3)已知函数图像,求函数解析式;
(4) 满足某个等式,这个等式除
满足某个等式,这个等式除 外还有其他未知量,需构造另个等式:解方程组法;
外还有其他未知量,需构造另个等式:解方程组法;
(5)应用题求函数解析式常用方法有待定系数法等。
题型1:函数概念
例1.(1)设函数
(2)(2001上海理,1)设函数f(x)=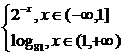 ,则满足f(x)=
,则满足f(x)=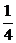 的x值为 。
的x值为 。
解:(1)这是分段函数与复合函数式的变换问题,需要反复进行数值代换,
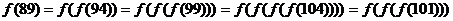
=
=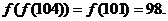
(2)当x∈(-∞,1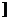 ,值域应为[
,值域应为[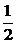 ,+∞],
,+∞],
当x∈(1,+∞)时值域应为(0,+∞),
∴y=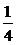 ,y∈(0,+∞),
,y∈(0,+∞),
∴此时x∈(1,+∞),
∴log81x=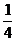 ,x=81
,x=81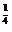 =3。
=3。
点评:讨论了函数的解析式的一些常用的变换技巧(赋值、变量代换、换元等等),这都是函数学习的常用基本功。
变式题:(2006山东 文2)设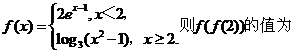 ( )
( )
A.0 B.1 C.2 D.3
解:选项为C。
例2.(2006安徽 文理15)
(1)函数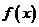 对于任意实数
对于任意实数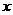 满足条件
满足条件 ,若
,若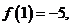 则
则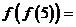 __ ________;
__ ________;
(2)函数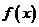 对于任意实数
对于任意实数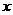 满足条件
满足条件 ,若
,若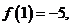 则
则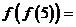 __________。
__________。
解:(1)由 得
得 ,
,
所以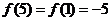 ,则
,则 。
。
(2)由 得
得 ,所以
,所以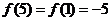 ,则
,则 。
。
点评:通过对抽象函数的限制条件,变量换元得到函数解析式,考察学生的逻辑思维能力。
题型二:判断两个函数是否相同
例3.试判断以下各组函数是否表示同一函数?
(1)f(x)=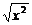 ,g(x)=
,g(x)=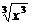 ;
;
(2)f(x)=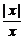 ,g(x)=
,g(x)=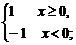
(3)f(x)= ,g(x)=(
,g(x)=( )2n-1(n∈N*);
)2n-1(n∈N*);
(4)f(x)=
 ,g(x)=
,g(x)= ;
;
(5)f(x)=x2-2x-1,g(t)=t2-2t-1。
解:(1)由于f(x)=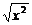 =|x|,g(x)=
=|x|,g(x)=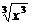 =x,故它们的值域及对应法则都不相同,所以它们不是同一函数;
=x,故它们的值域及对应法则都不相同,所以它们不是同一函数;
(2)由于函数f(x)=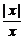 的定义域为(-∞,0)∪(0,+∞),而g(x)=
的定义域为(-∞,0)∪(0,+∞),而g(x)=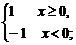 的定义域为R,所以它们不是同一函数;
的定义域为R,所以它们不是同一函数;
(3)由于当n∈N*时,2n±1为奇数,
∴f(x)= =x,g(x)=(
=x,g(x)=( )2n-1=x,它们的定义域、值域及对应法则都相同,所以它们是同一函数;
)2n-1=x,它们的定义域、值域及对应法则都相同,所以它们是同一函数;
(4)由于函数f(x)=
 的定义域为{x|x≥0},而g(x)=
的定义域为{x|x≥0},而g(x)= 的定义域为{x|x≤-1或x≥0},它们的定义域不同,所以它们不是同一函数;
的定义域为{x|x≤-1或x≥0},它们的定义域不同,所以它们不是同一函数;
(5)函数的定义域、值域和对应法则都相同,所以它们是同一函数。
点评:对于两个函数y=f(x)和y=g(x),当且仅当它们的定义域、值域、对应法则都相同时,y=f(x)和y=g(x)才表示同一函数 若两个函数表示同一函数,则它们的图象完全相同,反之亦然。
若两个函数表示同一函数,则它们的图象完全相同,反之亦然。
(1)第(5)小题易错判断成它们是不同的函数,原因是对函数的概念理解不透 要知道,在函数的定义域及对应法则f不变的条件下,自变量变换字母,以至变换成其他字母的表达式,这对于函数本身并无影响,比如f(x)=x2+1,f(t)=t2+1,f(u+1)=(u+1)2+1都可视为同一函数。(2)对于两个函数来讲,只要函数的三要素中有一要素不相同,则这两个函数就不可能是同一函数。
要知道,在函数的定义域及对应法则f不变的条件下,自变量变换字母,以至变换成其他字母的表达式,这对于函数本身并无影响,比如f(x)=x2+1,f(t)=t2+1,f(u+1)=(u+1)2+1都可视为同一函数。(2)对于两个函数来讲,只要函数的三要素中有一要素不相同,则这两个函数就不可能是同一函数。
题型三:函数定义域问题
例4.求下述函数的定义域:
(1) ;
;
(2)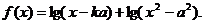
解:(1)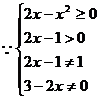 ,解得函数定义域为
,解得函数定义域为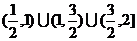 .
.
(2) ,(先对a进行分类讨论,然后对k进行分类讨论),
,(先对a进行分类讨论,然后对k进行分类讨论),
①当a=0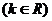 时,函数定义域为
时,函数定义域为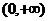 ;
;
②当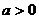 时,得
时,得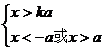 ,
,
1)当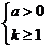 时,函数定义域为
时,函数定义域为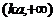 ,
,
2)当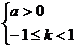 时,函数定义域为
时,函数定义域为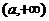 ,
,
3)当 时,函数定义域为
时,函数定义域为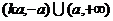 ;
;
③当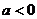 时,得
时,得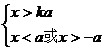 ,
,
1)当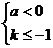 时,函数定义域为
时,函数定义域为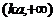 ,
,
2)当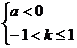 时,函数定义域为
时,函数定义域为 ,
,
3)当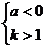 时,函数定义域为
时,函数定义域为 。
。
点评:在这里只需要根据解析式有意义,列出不等式,但第(2)小题的解析式中含有参数,要对参数的取值进行讨论,考察学生分类讨论的能力。
例5.已知函数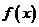 定义域为(0,2),求下列函数的定义域:
定义域为(0,2),求下列函数的定义域:
(1) 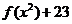 ;(2)
;(2)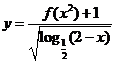 。
。
解:(1)由0<x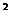 <2, 得
<2, 得
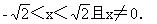
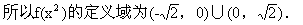

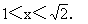
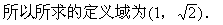
点评:本例不给出f(x)的解析式,即由f(x)的定义域求函数f[g(x)]的定义域 关键在于理解复合函数的意义,用好换元法;求函数定义域的第三种类型是一些数学问题或实际问题中产生的函数关系,求其定义域,后面还会涉及到。
关键在于理解复合函数的意义,用好换元法;求函数定义域的第三种类型是一些数学问题或实际问题中产生的函数关系,求其定义域,后面还会涉及到。
变式题:已知函数f(x)=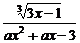 的定义域是R,则实数a的取值范围是( )
的定义域是R,则实数a的取值范围是( )
A.a>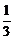 B.-12<a≤0 C.-12<a<0 D.a≤
B.-12<a≤0 C.-12<a<0 D.a≤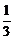
解:由a=0或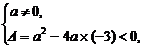 可得-12<a≤0,答案B。
可得-12<a≤0,答案B。
题型四:函数值域问题
例5.求下列函数的值域:
(1)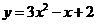 ;(2)
;(2)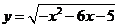 ;(3)
;(3)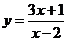 ;
;
(4)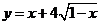 ;(5)
;(5)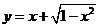 ;(6)
;(6)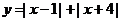 ;
;
(7)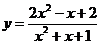 ;(8)
;(8)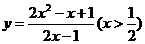 ;(9)
;(9)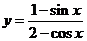 。
。
解:(1)(配方法)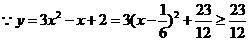 ,
,
∴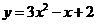 的值域为
的值域为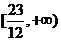 。
。
改题:求函数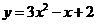 ,
,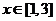 的值域。
的值域。
解:(利用函数的单调性)函数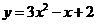 在
在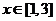 上单调增,
上单调增,
∴当 时,原函数有最小值为
时,原函数有最小值为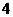 ;当
;当 时,原函数有最大值为
时,原函数有最大值为 。
。
∴函数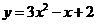 ,
,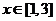 的值域为
的值域为 。
。
(2)求复合函数的值域:
设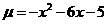 (
( ),则原函数可化为
),则原函数可化为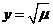 。
。
又∵ ,
,
∴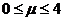 ,故
,故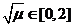 ,
,
∴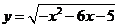 的值域为
的值域为 。
。
(3)(法一)反函数法:
 的反函数为
的反函数为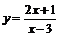 ,其定义域为
,其定义域为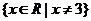 ,
,
∴原函数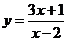 的值域为
的值域为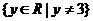 。
。
(法二)分离变量法: ,
,
∵ ,∴
,∴ ,
,
∴函数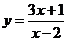 的值域为
的值域为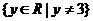 。
。
(4)换元法(代数换元法):设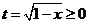 ,则
,则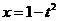 ,
,
∴原函数可化为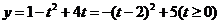 ,∴
,∴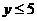 ,
,
∴原函数值域为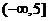 。
。
注:总结 型值域,
型值域,
变形: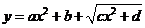 或
或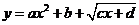
(5)三角换元法:
∵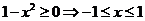 ,∴设
,∴设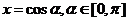 ,
,
则
∵ ,∴
,∴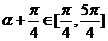 ,∴
,∴ ,
,
∴ ,
,
∴原函数的值域为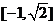 。
。
(6)数形结合法: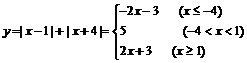 ,
,
∴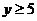 ,∴函数值域为
,∴函数值域为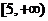 。
。
(7)判别式法:∵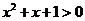 恒成立,∴函数的定义域为
恒成立,∴函数的定义域为 。
。
由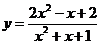 得:
得: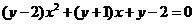 ①
①
①当 即
即 时,①即
时,①即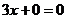 ,∴
,∴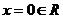
②当 即
即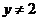 时,∵
时,∵ 时方程
时方程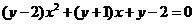 恒有实根,
恒有实根,
∴△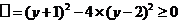 ,
,
∴ 且
且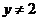 ,
,
∴原函数的值域为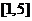 。
。
(8)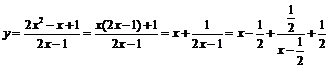 ,
,
∵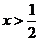 ,∴
,∴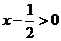 ,
,
∴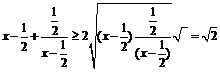 ,
,
当且仅当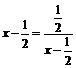 时,即
时,即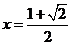 时等号成立。
时等号成立。
∴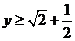 ,
,
∴原函数的值域为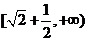 。
。
(9)(法一)方程法:原函数可化为: ,
,
∴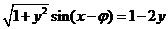 (其中
(其中 ),
),
∴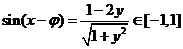 ,
,
∴ ,
,
∴ ,
,
∴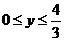 ,
,
∴原函数的值域为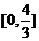 。
。
点评:上面讨论了用初等方法求函数值域的一些常见类型与方法,在现行的中学数学要求中,求值域要求不高,要求较高的是求函数的最大与最小值,在后面的复习中要作详尽的讨论。
题型五:函数解析式
例6.(1)已知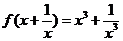 ,求
,求 ;
;
(2)已知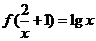 ,求
,求 ;
;
(3)已知 是一次函数,且满足
是一次函数,且满足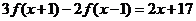 ,求
,求 ;
;
(4)已知 满足
满足 ,求
,求 。
。
解:(1)∵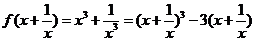 ,
,
∴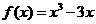 (
( 或
或 )。
)。
(2)令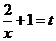 (
(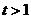 ),则
),则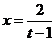 ,
,
∴ ,
,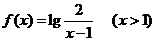 。
。
(3)设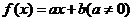 ,
,
则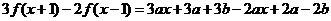
 ,
,
∴ ,
,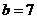 ,
,
∴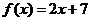 。
。
(4) ①,
①,
把①中的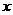 换成
换成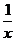 ,得
,得 ②,
②,
①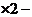 ②得
②得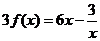 ,
,
∴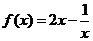 。
。
点评:第(1)题用配凑法;第(2)题用换元法;第(3)题已知一次函数,可用待定系数法;第(4)题用方程组法。
例7.(2006重庆理21)已知定义域为R的函数f(x)满足f(f(x)-x2+x)=f(x)-x2+x。
(Ⅰ)若f(2)=3,求f(1);又若f(0)=a,求f(a);
(Ⅱ)设有且仅有一个实数x0,使得f(x0)= x0。求函数f(x)的解析表达式。
解:(Ⅰ)因为对任意x∈R,有f(f(x)-x2 + x)=f(x)-x2 +x,
所以f(f(2)-22+2)=f(2)-22+2。
又由f(2)=3,得f(3-22+2)-3-22+2,即f(1)=1。
若f(0)=a,则f(a-02+0)=a-02+0,即f(a)=a。
(Ⅱ)因为对任意x∈R,有f(f(x))- x2 +x)=f(x)- x2 +x。
又因为有且只有一个实数x0,使得f(x0)- x0。
所以对任意x∈R,有f(x)- x2 +x= x0.。
在上式中令x= x0,有f(x0)-x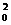 + x0= x0。
+ x0= x0。
又因为f(x0)- x0,所以x0-x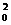 =0,故x0=0或x0=1。
=0,故x0=0或x0=1。
若x0=0,则f(x)- x2 +x=0,即f(x)= x2 –x。
但方程x2 –x=x有两上不同实根,与题设条件矛质,故x2≠0。
若x2=1,则有f(x)- x2 +x=1,即f(x)= x2 –x+1。
易验证该函数满足题设条件。
综上,所求函数为f(x)= x2 –x+1(x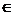 R)。
R)。
点评:该题的题设条件是一个抽象函数,通过应用条件进一步缩小函数的范围得到函数的解析式。这需要考生有很深的函数理论功底。
题型六:函数应用
例8.(2003北京春,理文21)某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出。当每辆车的月租金每增加50元时,未租出的车将会增加一辆。租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
解:(1)当每辆车的月租金定为3600元时,未租出的车辆数为:
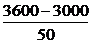 =12,所以这时租出了88辆车。
=12,所以这时租出了88辆车。
(2)设每辆车的月租金定为x元,则租赁公司的月收益为:
f(x)=(100- )(x-150)-
)(x-150)- ×50,
×50,
整理得:f(x)=-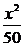 +162x-21000=-
+162x-21000=-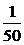 (x-4050)2+307050。
(x-4050)2+307050。
所以,当x=4050时,f(x)最大,其最大值为f(4050)=307050。
即当每辆车的月租金定为4050元时,租赁公司的月收益最大,最大收益为307050元.
点评:根据实际问题求函数表达式,是应用函数知识解决实际问题的基础,在设定或选定变量去寻求等量关系并求得函数表达式后,还要注意函数定义域常受到实际问题本身的限制。
例9.(2006湖南 理20)对1个单位质量的含污物体进行清洗,清洗前其清洁度(含污物体的清洁度定义为: 为
为 ,要求清洗完后的清洁度为
,要求清洗完后的清洁度为 。有两种方案可供选择,方案甲:一次清洗;方案乙:分两次清洗。该物体初次清洗后受残留水等因素影响,其质量变为
。有两种方案可供选择,方案甲:一次清洗;方案乙:分两次清洗。该物体初次清洗后受残留水等因素影响,其质量变为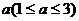 。设用
。设用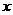 单位质量的水初次清洗后的清洁度是
单位质量的水初次清洗后的清洁度是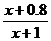
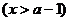 ,用
,用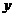 单位质量的水第二次清洗后的清洁度是
单位质量的水第二次清洗后的清洁度是 ,其中
,其中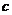
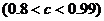 是该物体初次清洗后的清洁度。
是该物体初次清洗后的清洁度。
(Ⅰ)分别求出方案甲以及 时方案乙的用水量,并比较哪一种方案用水量较少;
时方案乙的用水量,并比较哪一种方案用水量较少;
(Ⅱ)若采用方案乙, 当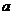 为某固定值时, 如何安排初次与第二次清洗的用水量,使总用水量最小? 并讨论
为某固定值时, 如何安排初次与第二次清洗的用水量,使总用水量最小? 并讨论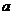 取不同数值时对最少总用水量多少的影响。
取不同数值时对最少总用水量多少的影响。
解:(Ⅰ)设方案甲与方案乙的用水量分别为x与z。
由题设有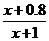 =0.99,解得x=19。
=0.99,解得x=19。
由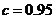 得方案乙初次用水量为3,
得方案乙初次用水量为3,
第二次用水量y满足方程: 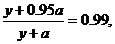 解得y=4
解得y=4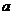 ,故z=4
,故z=4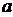 +3.即两种方案的用水量分别为19与4
+3.即两种方案的用水量分别为19与4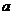 +3。
+3。
因为当 ,故方案乙的用水量较少。
,故方案乙的用水量较少。
(II)设初次与第二次清洗的用水量分别为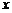 与
与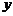 ,类似(I)得
,类似(I)得
 ,
,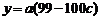 (*)
(*)
于是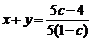 +
+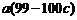
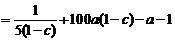
当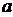 为定值时,
为定值时, ,
,
当且仅当 时等号成立。
时等号成立。
此时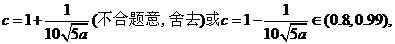
将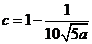 代入(*)式得
代入(*)式得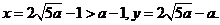
故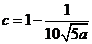 时总用水量最少,
时总用水量最少,
此时第一次与第二次用水量分别为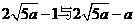 ,
,
最少总用水量是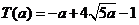 。
。
当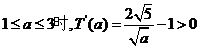 ,
,
故T(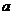 )是增函数(也可以用二次函数的单调性判断)。这说明,随着
)是增函数(也可以用二次函数的单调性判断)。这说明,随着 的值的最少总用水量, 最少总用水量最少总用水量。
的值的最少总用水量, 最少总用水量最少总用水量。
点评:本题贴近生活。要求考生读懂题目,迅速准确建立数学模型,把实际问题转化为数学问题并加以解决。该题典型代表高考的方向。
题型7:课标创新题
例10.(1)设 ,其中a、b、c、d是常数。
,其中a、b、c、d是常数。
如果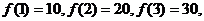 求
求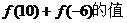 ;
;
(2)若不等式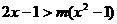 对满足
对满足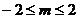 的所有m都成立,求x的取值范围。
的所有m都成立,求x的取值范围。
解:(1)构造函数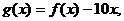 则
则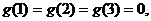 故:
故:
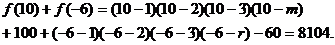
(2)原不等式可化为
构造函数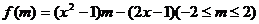 ,其图象是一条线段。
,其图象是一条线段。
根据题意,只须:

即
解得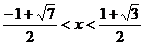 。
。
点评:上面两个题目通过重新构造函数解决了实际问题,体现了函数的工具作用。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com