程序每执行一次循环体，循环条件中涉及到的变量就会发生改变，正在步步逼近满足跳出循环体的条件。

程序中最忌“死循环”。所谓的“死循环”就是指该循环条件永远成立，没有跳出循环体的机会。

请看我们用WHILE循环实现1到100累加为例，做一下说明：

“1+2+……+100”

部分程序如下：

sum = 0

i =1

WHILE 　i <= 100

sum = sum+ i

i=i+1

WEND

这段程序中，循环的条件是“i <= 100”；因此，一开始i肯定需要一个确定的值。前面的

　“i = 0”这一个语句，在声明变量i的同时，也为i赋了初始值“1”。这样，条件 i <= 100 得以成立(因为i为1，所以 条件“i <= 100” 当然成立)。

3．学习了循环语句的两种格式，我们来挖掘一下应用循环语句编写程序的“条件三要素”。

2．条件语句的主要功能是来实现算法中的条件结构。

因为人们对计算机运算的要求不仅仅是一些简单的代数运算，而是经常需要计算机按照条件进行分析、比较、判断，并且按照判断后的不同情况进行不同的操作和处理。如果是要解决像“判断一个数的正负”、“比较数之间的大小”，“对一组数进行排序”、“求分段函数的函数值”等很多问题，计算机就需要用到条件语句。

在设计算法的过程中，解决问题的基本思想常常很简单、很清楚，但表述参与运算的数值的频频变换却很麻烦。为了解决这个问题，需要在程序中引入变量。前面通过对函数概念的学习，我们就已经了解变量的含义：在研究问题的过程中可以取代不同数值的量称为变量。

程序中一些重要的函数也很有用处，如取平方根函数SQR(x)=|x|，取绝对值函数ABS(x)=。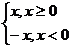

变量与函数是中学数学里面最重要的和最基本的概念，在算法的设计里面仍然发挥着重要的和最基本的作用，它们会使得算法的表达变得非常整洁、清楚。

1．赋值语句在程序运行时给变量赋值；“=”的右侧必须是表达式，左侧必须是变量；一个语句只能给一个变量赋值；有计算功能；将一个变量的值赋给另一个变量时，前一个变量的值保持不变；可先后给一个变量赋多个不同的值，但变量的取值只与最后一次赋值有关。

2．累加变量是最终的输出结果。每进入一次循环体随着计数变量改变而改变。累加变量的初始值通常为0。

1．计数变量的作用一般是统计循环体执行的次数，改变循环条件的取值，为结束循环作准备。譬如：计算等差、等比数列的前n项的和，n就是计数变量的临界值，在当型结构中“小于等于n”维持循环，而在直到型循环结构中“大于n”跳出循环。

2．条件语句的嵌套可多于两层，可以表达算法步骤中的多重限制条件。

题型4：循环语句

例7．设计一个计算1×3×5×7×…×99的算法，编写算法程序。

解析：

算法如下：

第一步：s＝1；

第二步：i＝3；

第三步：s＝s×i；

第四步：i＝i+2；

第五步：如果i≤99，那么转到第三步；

第六步：输出s；

程序如下：(“WHILE型”循环语句)

s＝1

i＝3

WHILE　 i＜＝99

s＝s*i

i＝i+2

WEND

PRINT　 s

END

点评：你能用“UNTIL”型循环语句表示“典例1”中的程序吗？

例8．编写一个程序，求1!+2!+…+10!的值。

解析：这个问题是求前10个正整数的阶乘之和，可以用“WHILE+ WHILE”循环嵌套语句格式来实现。

程序结构要做到如下步骤：

①处理“N!”的值；(注：处理N!值的变量就是一个内循环变量)

②累加“N!”的值。(注：累加N!值的变量就是一个外循环变量)

显然，通过10次循环可分别求出1!、2!、…、10!的值，并同时累加起来, 可求得S的值。而求T=N!，又可以用一个循环(内循环)来实现。

程序为:

s=0

i=1

WHILE i<=10

j=1

t=1

WHILE j<=i

t=t*j

j=j+1

WEND

s=s+t

i=i+1

WEND

PRINT s

END

上面程序中哪个变量是内循环变量，哪个变量是外循环变量？

(1)内循环变量：j，t

(2)外循环变量：s，i

“典例2”程序是一个的“WHILE+WHILE”型循环嵌套语句格式。这是一个比较好想的方法，但实际上对于求n!，我们也可以根据求出的(n－1)!乘上n即可得到，而无需重新从1再累乘到n。

程序可改为：

s=0

i=1

j=1

WHILE i<=10

j=j*i

s=s+j

i=i+1

WEND

PRINT s

END

显然第二个程序的效率要比第一个高得多。第一程序要进行1+2+…+10=55次循环，而第二程序进行10次循环。如题目中求的是1！+2！+…+1000！，则两个程序的效率区别更明显。

点评：解决具体的构造循环语句的算法问题，要尽可能的少引入循环变量，否则较多的变量会使得设计程序比较麻烦，并且较多的变量会使得计算机占用大量的系统资源，致使系统缓慢。另外，也尽可能使得循环嵌套的层数少，否则也浪费计算机的系统资源。

题型5：实际应用

例9．中国网通规定：拨打市内电话时，如果不超过3分钟，则收取话费0.22元；如果通话时间超过3分钟，则超出部分按每分钟0.1元收取通话费，不足一分钟按以一分钟计算。设通话时间为t(分钟)，通话费用y(元)，如何设计一个程序，计算通话的费用。

解析：

算法分析：

数学模型实际上为：y关于t的分段函数。

关系是如下：

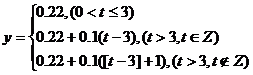
其中[t－3]表示取不大于t－3的整数部分。

算法步骤如下：

第一步：输入通话时间t；

第二步：如果t≤3，那么y = 0.22；否则判断t∈Z 是否成立，若成立执行y= 0.2+0.1× (t－3)；否则执行y = 0.2+0.1×( [t－3]+1)。

第三步：输出通话费用c 。

算法程序如下：

INPUT “请输入通话时间：”；t

IF　 t<=3　 THEN

y=0.22

ELSE

IF　 INT(t)=t　 THEN

y=0.22+0.1*(t－3)

ELSE

y=0.22+0.1*(INT(t－3)+1)

END IF

END IF

PRINT “通话费用为：”；y

END

点评：实际应用问题，在高考中是一个热点。如何将实际问题转化成数学问题是解题的关键，最后还要用算法步骤和程序进行表达。如：中国网通通话费的规定在数学中就是通话时间到通话费用的分段函数。日常生活中的分段函数问题还有很多：出租车的计费问题、个人所得税问题、银行利率问题等等。

例10．编写程序，计算数列{a_n}的前20项的和。(其中数列的前几项分别为1，1，2，3，5，8，……)

解析：这是“Fibonacci数列”的典型特征，从第三项起每一项都是它前两项的和，即。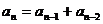

程序如下：

a=1

b=1

s=0

i=3

WHILE　 i<=20

s=s+a+b

t=a

a=b

b=b+t

i=i+1

WEND

PRINT s

END

点评：