
2.当总体中个体取不同值很少时,我们党用样本的频率分布标记频率分布梯形图取估计总体体分布,总体分布排除了抽样造成的错误,精确反映了总体取值的概率分布规律。对于所取不同数值较多或可以在实数区间范围内取值的总体,需用频率分布直方图来表示相应的频率分布。当样本容量无限增大,分组的组距无限缩小时,频率分布直方图无限接近一条光滑曲线--总体密度曲线.由于总体分布通常不易知道,往往是用样本的频率分布估计总体分布。样本容量越大,估计就越精确。
1.统计是为了从数据中提取信息,学习时根据实际问题的需求选择不同的方法合理地选取样本,并从样本数据中提取需要的数字特征。不应把统计处理成数字运算和画图表。对统计中的概念(如"总体"、"样本"等)应结合具体问题进行描述性说明,不应追求严格的形式化定义。
9.4 8.4 9.4 9.9 9.6 9.4 9.7
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为
(A)9.4, 0.484 (B)9.4, 0.016 (C)9.5, 0.04 (D)9.5, 0.016
答案:D;
解析:7个数据中去掉一个最高分和一个最低分后,余下的5个数为:9.4, 9.4, 9.6, 9.4, 9.5。
则平均数为: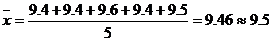 ,即
,即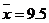 。
。
方差为: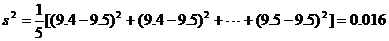
即 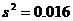 ,故选D。
,故选D。
点评:一定要根据实际的题意解决问题,并还原实际情景。
题型3:频率分布直方图与条形图
例5.为检测,某种产品的质量,抽取了一个容量为30的样本,检测结果为一级品5件,而极品8件,三级品13件,次品14件.
(1)列出样本频率分布表;
(2)画出表示样本频率分布的条形图;
(3)根据上述结果,估计辞呈商品为二极品或三极品的概率约是多少
解析:(1)样本的频率分布表为
|
产品 |
频数 |
频率 |
|
一级晶 |
5 |
0.17 |
|
二级晶 |
8 |
0.27 |
|
三级晶 |
13 |
0.43 |
|
次品 |
4 |
0.13 |
(2)样本频率分布的条形图为:
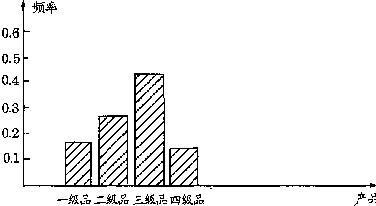
(3)此种产品为二极品或三极品的概率约为0.27+0.43=0.7。
点评:条形图中纵坐标一般是频数或频率。
例6.(2006重庆理,6)为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg) ,得到频率分布直方图如下:
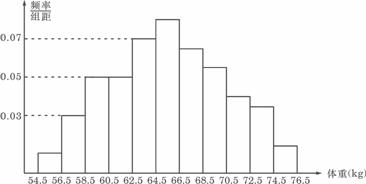
根据上图可得这100名学生中体重在(56.5,64.5)的学生人数是
(A)20 (B)30
(C)40 (D)50
答案:C;
解析:根据运算的算式:体重在(56.5,64.5)学生的累积频率为2×0.03+2×0.05+2×0.05+2×0.07=0.4,则体重在(56.5,64.5)学生的人数为0.4×100=40。
点评:熟悉频率、频数、组距间的关系式。
例7.某中学对高三年级进行身高统计,测量随机抽取的40名学生的身高,其结果如下(单位:cm)
|
分组 |
[140,145) |
[145,150) |
[150,155) |
[155,160) |
[160,165) |
[165,170) |
[170,175) |
[175,180) |
合计 |
|
人数 |
1 |
2 |
5 |
9 |
13 |
6 |
3 |
1 |
40 |
(1)列出频率分布表;
(2)画出频率分布直方图;
(3)估计数据落在[150,170]范围内的概率。
解析:(1)根据题意可列出频率分布表:
|
分 值 |
频 数 |
频 率 |
|
[140,145] |
1 |
0.025 |
|
[145,150] |
2 |
0.050 |
|
[150,155] |
5 |
0.125 |
|
[155,160] |
9 |
0.225 |
|
[160,165] |
13 |
0.325 |
|
[165,170] |
6 |
0.15 |
|
[170,175] |
3 |
0.075 |
|
[175,180] |
1 |
0.025 |
|
合 计 |
40 |
1.00 |
(2)频率分布直方图如下:
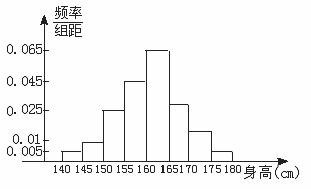
(3)数据落在[150,170]范围内的概率约为0.825。
题型4:茎叶图
例8.观看下面两名选手全垒打数据的茎叶图,对他们的表现进行比较。
1961年扬基队外垒手马利斯打破了鲁斯的一个赛季打出60个全垒打的记录。下面是扬基队的历年比赛中的鲁斯和马利斯每年击出的全垒打的比较图:

 鲁斯
马利斯
鲁斯
马利斯
0 8
1 3 4 6
5 2 2 3 6 8
5 4 3 3 9
9 7 6 6 1 1 4
9 4 4 5
0 6 1
解析:鲁斯的成绩相对集中,稳定在46左右;马利斯成绩相对发散,成绩稳定在26左右。
题型5:线性回归方程
例9.由施肥量x与水稻产量y试验数据的关系,画出散点图,并指明相关性。

解析:散点图为:

通过图象可知是正相关。
例10.在某种产品表面进行腐蚀线实验,得到腐蚀深度y与腐蚀时间t之间对应的一组数据:
|
时间t(s) |
5 |
10 |
15 |
20 |
30 |
40 |
50 |
60 |
70 |
90 |
120 |
深度y(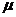 m) m) |
6 |
10 |
10 |
13 |
16 |
17 |
19 |
23 |
25 |
29 |
46 |
(1)画出散点图;
(2)试求腐蚀深度y对时间t的回归直线方程。
略解:(1)散点图略,呈直线形。
(2)经计算可得
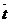 =46.36,
=46.36,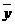 =19.45,
=19.45,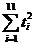 =36750,
=36750,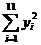 =5442,
=5442, =13910。
=13910。
B=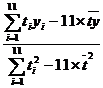 =
=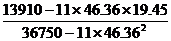
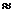 0.3.
0.3.
A=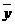 -b
-b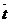 =19.45-03
=19.45-03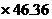
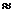 5.542。
5.542。
故所求的回归直线方程为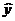 =0.3t+5.542。
=0.3t+5.542。
题型6:创新题
例11.把容量为100的某个样本数据分为10组,并填写频率分布表,若前七组的累积频率为0.79,而剩下三组的频数成公比大于2的整数等比数列,则剩下三组中频数最高的一组的频数为___________.
答案:16
点评:已知前七组的累积频率为0.79,而要研究后三组的问题,因此应先求出后三组的频率之和为1-0.79=0.21,进而求出后三组的共有频数,或者先求前七组共有频数后,再计算后三组的共有频数。由已知知前七组的累积频数为0.79×100=79,故后三组共有的频数为21,依题意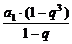 =21,a1(1+q+q2)=21.∴a1=1,q=4。∴后三组频数最高的一组的频数为16。此题剖析只按第二种思路给出了解答,你能按第一种思路来解吗?
=21,a1(1+q+q2)=21.∴a1=1,q=4。∴后三组频数最高的一组的频数为16。此题剖析只按第二种思路给出了解答,你能按第一种思路来解吗?
例12.某班学生在一次数学考试中成绩分布如下表:
|
分数段 |
[0,80) |
[80,90) |
[90,100) |
||
|
人数 |
2 |
|
6 |
||
|
分数段 |
[100,110) |
[110,120 |
[120,130) |
||
|
人数 |
8 |
12 |
6 |
||
|
分数段 |
[130,140) |
[140,150) |
|
||
|
人数 |
4 |
2 |
|
那么分数在[100,110)中的频率和分数不满110分的累积频率分别是______________、_______(精确到0.01).
解析:由频率计算方法知:总人数=45.
分数在[100,110)中的频率为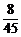 =0.178≈0.18.
=0.178≈0.18.
分数不满110分的累积频率为 =
=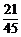 ≈0.47.
≈0.47.
答案:0.18 0.47
1.7 1.2 2.1 3.2 1.0
(1)通过对样本的计算,估计该县1999年消耗了多少盒一次性筷子(每年按350个营业日计算);
(2)2001年又对该县一次性木质筷子的用量以同样的方式作了抽样调查,调查的结果是10个样本饭店,每个饭店平均每天使用一次性筷子2.42盒.求该县2000年、2001年这两年一次性木质筷子用量平均每年增长的百分率(2001年该县饭店数、全年营业天数均与1999年相同);
(3)在(2)的条件下,若生产一套学生桌椅需木材0.07m3,求该县2001年使用一次性筷子的木材可以生产多少套学生桌椅。计算中需用的有关数据为:每盒筷子100双,每双筷子的质量为5g,所用木材的密度为0.5×103kg/m3;
(4)假如让你统计你所在省一年使用一次性筷子所消耗的木材量,如何利用统计知识去做,简要地用文字表述出来。
解析:(1)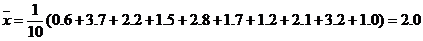
所以,该县1999年消耗一次性筷子为2×600×350=420000(盒)。
(2)设平均每年增长的百分率为X,则2(1+X)2=2.42,
解得X1=0.1=10%,X2=-2.1(不合题意,舍去)。
所以,平均每年增长的百分率为10%;
(3)可以生产学生桌椅套数为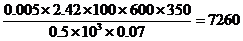 (套)。
(套)。
(4)先抽取若干个县(或市、州)作样本,再分别从这些县(或市、州)中抽取若干家饭店作样本,统计一次性筷子的用量.
点评:本题是一道统计综合题,涉及的知识点很多,需要灵活运用各种知识分析解决问题.对于第(1)小题,可先求得样本平均数,再利用样本估计总体的思想来求得问题的解.对于第(2)小题,实际是一个增长率问题的应用题,可通过设未知数列方程的方法来解.对于第(3)小题,用到了物理公式m=ρv, 体现了各学科知识之间的联系,让学生触类旁通,在解决实际问题时能综合运用多种知识灵活地解决问题.第(4)小题只要能够运用随机抽样方法,能体会到用样本估计总体的统计思想就可解决,在文字表述上要注意简洁、明了、正确。
题型2:数字特征的应用
例3.(2002年全国高考天津文科卷(15))甲、乙两种冬小麦试验品种连续5年的平均单位面积产量如下(单位:t / hm2)
|
品种 |
第1年 |
第2年 |
第3年 |
第4年 |
第5年 |
|
甲 |
9.8 |
9.9 |
10.1 |
10 |
10.2 |
|
乙 |
9.4 |
10.3 |
10.8 |
9.7 |
9.8 |
其中产量比较稳定的小麦品种是 甲 。
解析:¯甲 = 1 5( 9.8 + 9.9 + 10.1 + 10 + 10.2) = 10.0,¯乙 = 1 5( 9.4 + 10.3 + 10.8 + 9.7 + 9.8) = 10.0;
s 2甲 = 1 5( 9.82 + … + 10.22) – 102 = 0.02,s 2甲 = 1 5( 9.42 + … + 9.82) – 102 = 0.244 > 0.02 。
点评:方差与平均数在反映样本的特征上一定要区分开。
例4.(2005江苏7)在一次歌手大奖赛上,七位评委为歌手打出的分数如下:
题型1:数字特征
例1.为了检查一批手榴弹的杀伤半径,抽取了其中20颗做试验,得到这20颗手榴弹的杀伤半径,并列表如下:

(1)在这个问题中,总体、个体、样本和样本容量各是什么?
(2)求出这20颗手榴弹的杀伤半径的众数、中位数和平均数,并估计这批手榴弹的平均杀伤半径.
解析: (1)总体是要检查的这批手榴弹的杀伤半径的全体;个体是每一颗手榴弹的杀伤半径;样本是所抽取的20颗手榴弹的杀伤半径;样本容量是20。
(2)在20个数据中,10出现了6次,次数最多,所以众数是10(米)。
20个数据从小到大排列,第10个和第11个数据是最中间的两个数,分别为9(米)和10(米),所以中位数是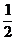 (9+10)=9.5(米)。
(9+10)=9.5(米)。
样本平均数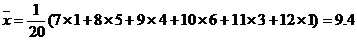 (米)
(米)
所以,估计这批手榴弹的平均杀伤半径约为9.4米。
点评:(1)根据总体、个体、样本、样本容量的概念答题.要注意:总体、个体和样本所说的考察对象是一种数量指标,不能说成考察的对象是手榴弹,而应说是手榴弹的杀伤半径。
(2)读懂表格的意义,利用概念求众数、中位数,用样本平均数估计这批手榴弹的平均杀伤半径.另外在这里要会简便计算有多个重复数据的样本的平均数。
例2.为估计一次性木质筷子的用量,1999年从某县共600家高、中、低档饭店抽取10家作样本,这些饭店每天消耗的一次性筷子盒数分别为:
0.6 3.7 2.2 1.5 2.8
3.线性回归
回归分析:对于两个变量,当自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫相关关系或回归关系。
回归直线方程:设x与y是具有相关关系的两个变量,且相应于n个观测值的n个点大致分布在某一条直线的附近,就可以认为y对x的回归函数的类型为直线型: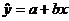 。其中
。其中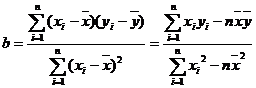 ,
,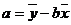 。我们称这个方程为y对x的回归直线方程。
。我们称这个方程为y对x的回归直线方程。
2.频率分布直方图、折线图与茎叶图
样本中所有数据(或数据组)的频率和样本容量的比,就是该数据的频率。所有数据(或数据组)的频率的分布变化规律叫做频率分布,可以用频率分布直方图、折线图、茎叶图来表示。
频率分布直方图:
具体做法如下:
(1)求极差(即一组数据中最大值与最小值的差);
(2)决定组距与组数;
(3)将数据分组;
(4)列频率分布表;
(5)画频率分布直方图。
注:频率分布直方图中小正方形的面积=组距× =频率。
=频率。
折线图:连接频率分布直方图中小长方形上端中点,就得到频率分布折线图。
总体密度曲线:当样本容量足够大,分组越多,折线越接近于一条光滑的曲线,此光滑曲线为总体密度曲线。
1.用样本的数字特征估计总体的数字特征
(1)众数、中位数
在一组数据中出现次数最多的数据叫做这组数据的众数;
将一组数据按照从大到小(或从小到大)排列,处在中间位置上的一个数据(或中间两位数据的平均数)叫做这组数据的中位数;
(2)平均数与方差
如果这n个数据是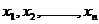 ,那么
,那么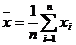 叫做这n个数据平均数;
叫做这n个数据平均数;
如果这n个数据是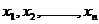 ,那么
,那么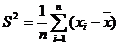 叫做这n个数据方差;同时
叫做这n个数据方差;同时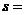
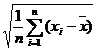 叫做这n个数据的标准差。
叫做这n个数据的标准差。
2.热点问题是频率分布直方图和用样本的数字特征估计总体的数字特征。
“统计”是在初中“统计初步”基础上的深化和扩展,本讲主要会用样本的频率分布估计总体的分布,并会用样本的特征来估计总体的分布。
预测2007年高考对本讲的考察是:
1.以基本题目(中、低档题)为主,多以选择题、填空题的形式出现,以实际问题为背景,综合考察学生学习基础知识、应用基础知识、解决实际问题的能力;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com