
2.基本不等式
定理1:如果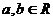 ,那么
,那么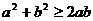 (当且仅当
(当且仅当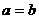 时取“
时取“ ”)。
”)。
说明:(1)指出定理适用范围: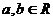 ;(2)强调取“
;(2)强调取“ ”的条件
”的条件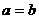 。
。
定理2:如果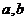 是正数,那么
是正数,那么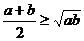 (当且仅当
(当且仅当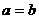 时取“=”)
时取“=”)
说明:(1)这个定理适用的范围: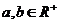 ;(2)我们称
;(2)我们称 的算术平均数,称
的算术平均数,称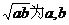 的几何平均数。即:两个正数的算术平均数不小于它们的几何平均数。
的几何平均数。即:两个正数的算术平均数不小于它们的几何平均数。
1.不等式的性质
比较两实数大小的方法--求差比较法
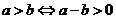 ;
;
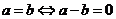 ;
;
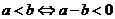 。
。
定理1:若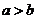 ,则
,则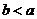 ;若
;若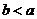 ,则
,则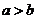 .即
.即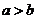
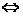
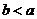 。
。
说明:把不等式的左边和右边交换,所得不等式与原不等式异向,称为不等式的对称性。
定理2:若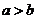 ,且
,且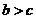 ,则
,则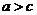 。
。
说明:此定理证明的主要依据是实数运算的符号法则及两正数之和仍是正数;定理2称不等式的传递性。
定理3:若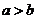 ,则
,则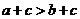 。
。
说明:(1)不等式的两边都加上同一个实数,所得不等式与原不等式同向;
(2)定理3的证明相当于比较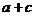 与
与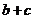 的大小,采用的是求差比较法;
的大小,采用的是求差比较法;
(3)定理3的逆命题也成立;
(4)不等式中任何一项改变符号后,可以把它从一边移到另一边。
定理3推论:若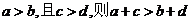 。
。
说明:(1)推论的证明连续两次运用定理3然后由定理2证出;(2)这一推论可以推广到任意有限个同向不等式两边分别相加,即:两个或者更多个同向不等式两边分别相加,所得不等式与原不等式同向;(3)同向不等式:两个不等号方向相同的不等式;异向不等式:两个不等号方向相反的不等式。
定理4.如果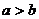 且
且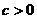 ,那么
,那么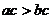 ;如果
;如果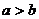 且
且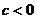 ,那么
,那么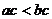 。
。
推论1:如果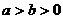 且
且 ,那么
,那么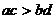 。
。
说明:(1)不等式两端乘以同一个正数,不等号方向不变;乘以同一个负数,不等号方向改变;(2)两边都是正数的同向不等式的两边分别相乘,所得不等式与原不等式同向;(3)推论 可以推广到任意有限个两边都是正数的同向不等式两边分别相乘。这就是说,两个或者更多个两边都是正数的同向不等式两边分别相乘,所得不等式与原不等式同向。
可以推广到任意有限个两边都是正数的同向不等式两边分别相乘。这就是说,两个或者更多个两边都是正数的同向不等式两边分别相乘,所得不等式与原不等式同向。
推论2:如果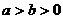 , 那么
, 那么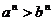
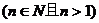 。
。
定理5:如果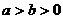 ,那么
,那么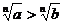
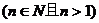 。
。
2.利用基本不等式解决像函数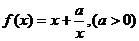 的单调性或解决有关最值问题是考察的重点和热点,应加强训练。
的单调性或解决有关最值问题是考察的重点和热点,应加强训练。
不等式历来是高考的重点内容。对于本将来讲,考察有关不等式性质的基础知识、基本方法,而且还考察逻辑推理能力、分析问题、解决问题的能力。本将内容在复习时,要在思想方法上下功夫。
预测2007年的高考命题趋势:
1.从题型上来看,选择题、填空题都有可能考察,把不等式的性质与函数、三角结合起来综合考察不等式的性质、函数单调性等,多以选择题的形式出现,解答题以含参数的不等式的证明、求解为主;
2.基本不等式:(a,b≥0)
①探索并了解基本不等式的证明过程;
②会用基本不等式解决简单的最大(小)问题。
1.不等关系
通过具体情境,感受在现实世界和日常生活中存在着大量的不等关系,了解不等式(组)的实际背景;
3.数学思想
(1)迭加累加(等差数列的通项公式的推导方法)若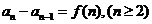 ,则……;
,则……;
(2)迭乘累乘(等比数列的通项公式的推导方法)若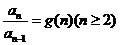 ,则……;
,则……;
(3)逆序相加(等差数列求和公式的推导方法);
(4)错位相减(等比数列求和公式的推导方法)。
2.常用结论
(1)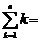 1+2+3+...+n =
1+2+3+...+n = 
(2)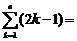 1+3+5+...+(2n-1) =
1+3+5+...+(2n-1) =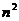
(3)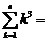

(4)
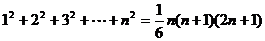
(5)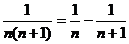
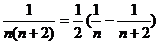
(6)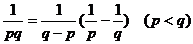
1.数列求和的常用方法
(1)公式法:适用于等差、等比数列或可转化为等差、等比数列的数列;
(2)裂项相消法:适用于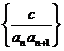 其中{
其中{ 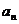 }是各项不为0的等差数列,c为常数;部分无理数列、含阶乘的数列等;
}是各项不为0的等差数列,c为常数;部分无理数列、含阶乘的数列等;
(3)错位相减法:适用于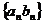 其中{
其中{ 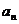 }是等差数列,
}是等差数列,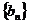 是各项不为0的等比数列。
是各项不为0的等比数列。
(4)倒序相加法:类似于等差数列前n项和公式的推导方法.
(5)分组求和法
(6)累加(乘)法等。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com