
2.根据函数零点的意义探索研究二次函数的零点情况,并进行交流,总结概括形成结论.
二次函数的零点:
二次函数
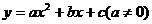 .
.
(1)△>0,方程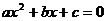 有两不等实根,二次函数的图象与
有两不等实根,二次函数的图象与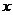 轴有两个交点,二次函数有两个零点.
轴有两个交点,二次函数有两个零点.
(2)△=0,方程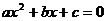 有两相等实根(二重根),二次函数的图象与
有两相等实根(二重根),二次函数的图象与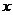 轴有一个交点,二次函数有一个二重零点或二阶零点.
轴有一个交点,二次函数有一个二重零点或二阶零点.
(3)△<0,方程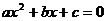 无实根,二次函数的图象与
无实根,二次函数的图象与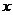 轴无交点,二次函数无零点.
轴无交点,二次函数无零点.
函数零点的概念:
对于函数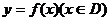 ,把使
,把使 成立的实数
成立的实数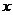 叫做函数
叫做函数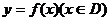 的零点.
的零点.
函数零点的意义:
函数 的零点就是方程
的零点就是方程 实数根,亦即函数
实数根,亦即函数 的图象与
的图象与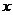 轴交点的横坐标.
轴交点的横坐标.
即:
方程 有实数根
有实数根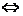 函数
函数 的图象与
的图象与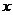 轴有交点
轴有交点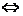 函数
函数 有零点.
有零点.
函数零点的求法:
求函数 的零点:
的零点:
①(代数法)求方程 的实数根;
的实数根;
②(几何法)对于不能用求根公式的方程,可以将它与函数 的图象联系起来,并利用函数的性质找出零点.
的图象联系起来,并利用函数的性质找出零点.
1.师:引导学生仔细体会左边的这段文字,感悟其中的思想方法.
生:认真理解函数零点的意义,并根据函数零点的意义探索其求法:
①代数法;
②几何法.
1.师:引导学生解方程,画函数图象,分析方程的根与图象和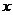 轴交点坐标的关系,引出零点的概念.
轴交点坐标的关系,引出零点的概念.
生:独立思考完成解答,观察、思考、总结、概括得出结论,并进行交流.
师:上述结论推广到一般的一元二次方程和二次函数又怎样?
2.先来观察几个具体的一元二次方程的根及其相应的二次函数的图象:
(用投影仪给出)
①方程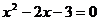 与函数
与函数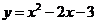
②方程 与函数
与函数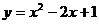
③方程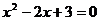 与函数
与函数
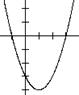
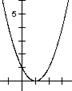
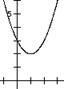
1、提出问题:一元二次方程 ax2+bx+c=0 (a≠0)的根与二次函数
y=ax2+bx+c(a≠0)的图象有什么关系?
17.解:(1)证明联立的方程有两解即可
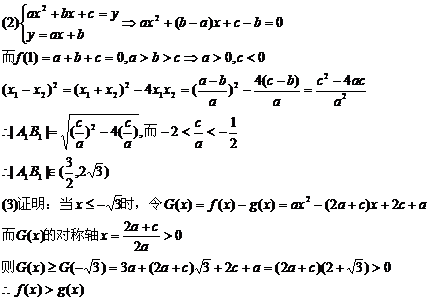
天星 教育网() 版权所有
天星 教育网() 版权所有
天星 教育网() 版权所有
|
|
|
|||||||||||||||
 |
|||||||||||||||
|
|||||||||||||||
|
|||||||||||||||
 |
|||||||||||||||
 |
|||||||||||||||
 |
|||||||||||||||
 |
16.解:(1)
(2)
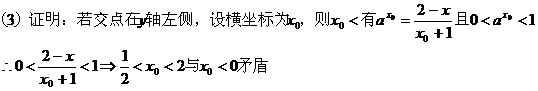
15.解:(1)奇函数. (2)
15.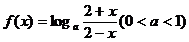 已知函数
已知函数
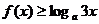
(1)试判断函数f(x)的奇偶性, (2)解不等式
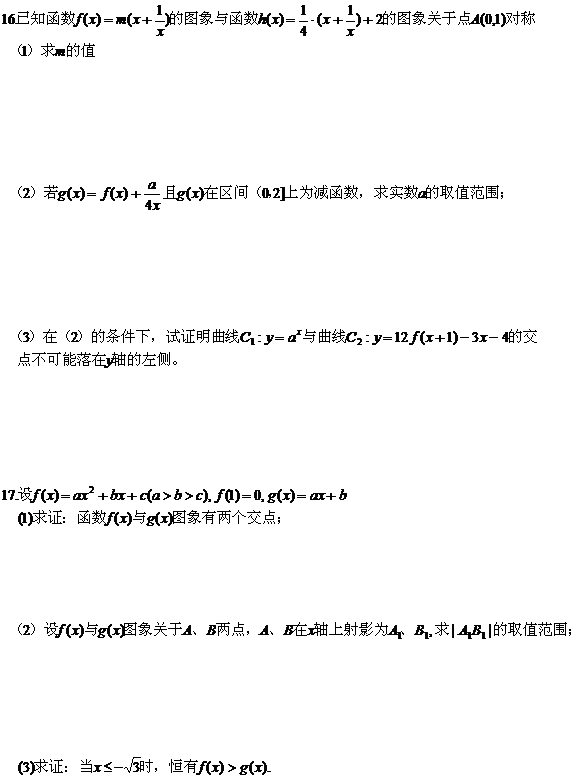
函数图形和性质答案(答案)
12.二次函数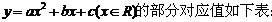
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
y |
6 |
0 |
-4 |
-6 |
-6 |
-4 |
0 |
6 |

则不等式
 三、解答题
三、解答题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com