

2.(2003北京)若数列{an}的通项公式是
an= ,n=1,2,…,则
,n=1,2,…,则 (a1+a2+…+an)等于
(a1+a2+…+an)等于
A. B.
B. C.
C.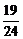 D.
D.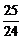
1.
 [n(1-
[n(1-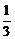 )(1-
)(1-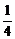 )(1-
)(1- )…(1-
)…(1- )]等于 ( )
)]等于 ( )
A.0 B.1 C.2 D.3
4.在日常学习过程中,注意化归思想、分类讨论思想和极限思想的运用.
同步练习
[选择题]
3. 对含参数的题目要看是否需要分类讨论;
2. 对  型的极限,要分别通过“约去使分母为零的因式、同除以分子、分母的最高次幂、有理化分子”等变形,化归转化后再求极限值。
型的极限,要分别通过“约去使分母为零的因式、同除以分子、分母的最高次幂、有理化分子”等变形,化归转化后再求极限值。
1. 极限的四则运算法则只用于有限次的运算,对于n项和的极限,要先求和再求极限;
[例1] 求下列极限:
(1)
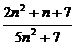 ; (2)
; (2)  (
(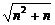 -n);
-n);
(3) (
(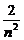 +
+ +…+
+…+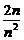 ).
).
分析:(1)因为分子分母都无极限,故不能直接运用商的极限运算法则,可通过变形分子分母同除以n2后再求极限;(2)因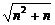 与n都没有极限,可先分子有理化再求极限;(3)因为极限的运算法则只适用于有限个数列,需先求和再求极限.
与n都没有极限,可先分子有理化再求极限;(3)因为极限的运算法则只适用于有限个数列,需先求和再求极限.
解:(1)
 =
=
 =
=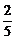 .
.
(2) (
(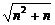 -n)=
-n)= 
 =
=
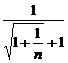 =
= .
.
(3)原式=
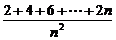 =
=
 =
= (1+
(1+ )=1.
)=1.
◆特别提示::对于(1)要避免下面两种错误:①原式=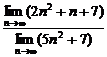 =
= =1,②∵
=1,②∵ (2n 2+n+7),
(2n 2+n+7),  (5n2+7)不存在,∴原式无极限.对于(2)要避免出现下面两种错误:
①
(5n2+7)不存在,∴原式无极限.对于(2)要避免出现下面两种错误:
① (
(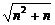 -n)=
-n)= 
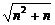 -
- n=∞-∞=0;②原式=
n=∞-∞=0;②原式=
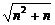 -
- n=∞-∞不存在.对于(3)要避免出现原式=
n=∞-∞不存在.对于(3)要避免出现原式=
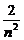 +
+
 +…+
+…+
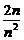 =0+0+…+0=0这样的错误.
=0+0+…+0=0这样的错误.
[例2] 已知数列{an}是由正数构成的数列,a1=3,且满足lgan=lgan-1+lgc,其中n是大于1的整数,c是正数.
(1)求数列{an}的通项公式及前n和Sn;
(2)求
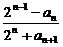 的值.
的值.
解:(1)由已知得an=c·an-1,
∴{an}是以a1=3,公比为c的等比数列,则an=3·cn-1.
∴Sn=
(2)

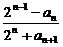 =
=
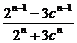 .
.
①当c=2时,原式=-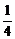 ;
;
②当c>2时,原式=
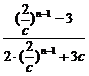 =-
=-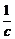 ;
;
③当0<c<2时,原式=
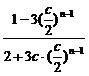 =
= .
.
评述:求数列极限时要注意分类讨论思想的应用.
[例3]
已知直线l:x-ny=0(n∈N *),圆M:(x+1)2+(y+1)2=1,抛物线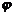 :y=(x-1)2,又l与M交于点A、B,l与
:y=(x-1)2,又l与M交于点A、B,l与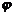 交于点C、D,求
交于点C、D,求
 .
.
分析:要求
 的值,必须先求它与n的关系.
的值,必须先求它与n的关系.
解:设圆心M(-1,-1)到直线l的距离为d,则d2=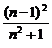 .
.
又r=1,∴|AB|2=4(1-d2)=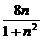 .
.
设点C(x1,y1), D(x2,y2),
由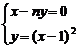
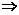 nx2-(2n+1)x+n=0,
nx2-(2n+1)x+n=0,
∴x1+x2= , x1·x2=1.
, x1·x2=1.
∵(x1-x2)2=(x1+x2)2-4x1x2= ,(y1-y2)2=(
,(y1-y2)2=(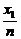 -
-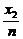 )2=
)2=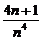 ,
,
∴|CD|2=(x1-x2)2+(y1-y2)2
=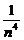 (4n+1)(n2+1).
(4n+1)(n2+1).
∴
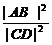 =
=
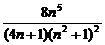 =
=
 =2.
=2.
评述:本题属于解析几何与数列极限的综合题.要求极限,需先求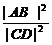 ,这就要求掌握求弦长的方法.
,这就要求掌握求弦长的方法.
[例4]若数列{an}的首项为a1=1,且对任意n∈N*,an与an+1恰为方程x2-bnx+cn=0的两根,其中0<|c|<1,当 (b1+b2+…+bn)≤3时,求c的取值范围.
(b1+b2+…+bn)≤3时,求c的取值范围.
解:首先,由题意对任意n∈N*,an·an+1=cn恒成立.
∴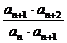 =
=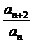 =
=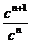 =c.又a1·a2=a2=c.
=c.又a1·a2=a2=c.
∴a1,a3,a5,…,a2n-1,…是首项为1,公比为c的等比数列,a2,a4,a6,…,a2n,…是首项为c,公比为c的等比数列.其次,由于对任意n∈N*,an+an+1=bn恒成立.
∴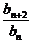 =
=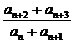 =c.又b1=a1+a2=1+c,b2=a2+a3=2c,
=c.又b1=a1+a2=1+c,b2=a2+a3=2c,
∴b1,b3,b5,…,b2n-1,…是首项为1+c,公比为c的等比数列,b2,b4,b6,…,b2n,…是首项为2c,公比为c的等比数列,
∴ (b1+b2+b3+…+bn)
(b1+b2+b3+…+bn)
=  (b1+b3+b5+…)+
(b1+b3+b5+…)+  (b2+b4+…)
(b2+b4+…)
= +
+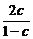 ≤3.
≤3.
解得c≤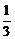 或c>1.∵0<|c|<1,∴0<c≤
或c>1.∵0<|c|<1,∴0<c≤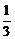 或-1<c<0.
或-1<c<0.
故c的取值范围是(-1,0)∪(0,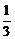 ].
].
提炼方法: 本题的解题目标是将题设中的极限不等式转化为关于c的不等式,即将{bn}的各项和表示为关于c的解析式;关键是对数列特点的分析和运用;显然“起点”应是一元二次方程根与系数的关系.
[研讨.欣赏]在大沙漠上进行勘测工作时,先选定一点作为坐标原点,然后采用如下方法进行:从原点出发,在x轴上向正方向前进a(a>0)个单位后,向左转90°,前进a r (0<r<1=个单位,再向左转90°,又前进a r2个单位,…,如此连续下去.
(1)若有一小分队出发后与设在原点处的大本营失去联系,且可以断定此小分队的行动与原定方案相同,则大本营在何处寻找小分队?
(2)若其中的r为变量,且0<r<1,则行动的最终目的地在怎样的一条曲线上?
剖析:(1)小分队按原方案走,小分队最终应在运动的极限位置.
(2)可先求最终目的地关于r的参数形式的方程.
解:(1)由已知可知即求这样运动的极限点,设运动的极限位置为Q(x,y),则
x=a-ar2+ar4-…=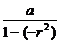 =
=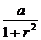 ,
,
y=ar-ar3+ar5-…=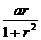 ,
,
∴大本营应在点(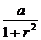 ,
,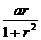 )附近去寻找小分队.
)附近去寻找小分队.
(2)由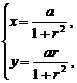 消去r得(x-
消去r得(x- )2+y2=
)2+y2=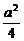 (其中x>
(其中x> ,y>0),
,y>0),
即行动的最终目的地在以( ,0)为圆心,
,0)为圆心, 为半径的圆上.
为半径的圆上.
6. -1
5.  =0.12+0.0012+…=0.12/(1─0.01) =4/33.
=0.12+0.0012+…=0.12/(1─0.01) =4/33.
4.  .分子先求和,再求极限.
.分子先求和,再求极限.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com