
6. 把n个不同的球随机地放入编号为1,2,…,m的m个盒子内,则1号盒恰有r个球的概率等于__________.
简答.提示:1-3.BDC; 3.由C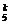 (
(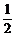 )k(
)k(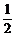 )5-k=C
)5-k=C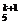 (
(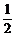 )k+1·(
)k+1·(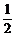 )5-k-1,
)5-k-1,
即C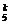 =C
=C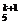 ,k+(k+1)=5,k=2; 4.他须解对5题或4题.P=(
,k+(k+1)=5,k=2; 4.他须解对5题或4题.P=(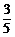 )5+C
)5+C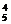 ×(
×(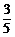 )4×(1-
)4×(1-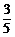 )=
)=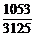 ; 5.
; 5. ;
;
5.甲、乙两人在罚球线投球命中的概率分别为 ,甲、乙两人在罚球线各投球二次,这四次中至少一次命中的概率是________.
,甲、乙两人在罚球线各投球二次,这四次中至少一次命中的概率是________.
4.某学生参加一次选拔考试,有5道题,每题10分.已知他解题的正确率为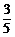 ,若40分为最低分数线,则该生被选中的概率是________.
,若40分为最低分数线,则该生被选中的概率是________.
3.将一枚硬币连掷5次,如果出现k次正面的概率等于出现k+1次正面的概率,那么k的值为 ( )
A.0 B.1 C.2 D.3
[填空题]
2.在某段时间内,甲地不下雨的概率为0.3,乙地不下雨的概率为0.4,假设在这段时间内两地是否下雨相互无影响,则这段时间内两地都下雨的概率是 ( )
A.0.12 B.0.88 C.0.28 D.0.42
1.(2004年辽宁,5)甲、乙两人独立地解同一问题,甲解决这个问题的概率是p1,乙解决这个问题的概率是p2,那么恰好有1人解决这个问题的概率是
A.p1p2 B.p1(1-p2)+p2(1-p1)
C.1-p1p2 D.1-(1-p1)(1-p2)
3.善于发现或将问题化为n次独立重复试验问题,进而计算发生k次的概率.
同步练习 10.7相互独立事件同时发生的概率
[选择题]
2.对于复杂的事件要能将其分解为互斥事件的和或独立事件的积,或先计算对立事件.
1.正确理解概念,能准确判断是否相互独立事件,只有对于相互独立事件A与B来说,才能运用公式P(A·B)=P(A)·P(B).
[例1]甲、乙两人各进行3次射击,甲每次击中目标的概率为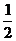 ,乙每次击中目标的概率为
,乙每次击中目标的概率为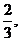 求:
求:
(Ⅰ)甲恰好击中目标2次的概率;
(Ⅱ)乙至少击中目标2次的概率;
(Ⅲ)乙恰好比甲多击中目标2次的概率.
解:(I)甲恰好击中目标2次的概率为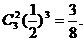
(II)乙至少击中目标2次的概率为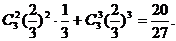
(III)设乙恰好比甲多击中目标2次为事件A,乙恰好击中目标2次且甲恰好击中目标0次为事件B1,乙恰好击中目标3次且甲恰好击中目标1次为事件B2,则A=B1+B2,B1,B2为互斥事件.
P(A)=P(B1)+P(B2)
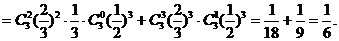
所以,乙恰好比甲多击中目标2次的概率为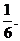
[例2](2006浙江)甲、乙两袋装有大小相同的红球和白球,甲袋装有2个红球,2个白球;乙袋装有2个红球,n个白球.两甲,乙两袋中各任取2个球.
(Ⅰ)若n=3,求取到的4个球全是红球的概率;
(Ⅱ)若取到的4个球中至少有2个红球的概率为 ,求n.
,求n.
解:(I)记“取到的4个球全是红球”为事件 .
.
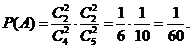
(II)记“取到的4个球至多有1个红球”为事件 ,“取到的4个球只有1个红球”为事件
,“取到的4个球只有1个红球”为事件 ,“取到的4个球全是白球”为事件
,“取到的4个球全是白球”为事件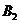 .
.
由题意,得


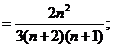
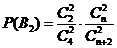
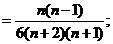 所以
所以
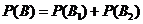
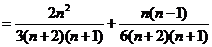
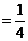 ,
,
化简,得 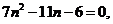
解得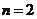 ,或
,或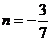 (舍去),故
(舍去),故 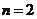 .
.
[例3](2006四川)某课程考核分理论与实验两部分进行,每部分考核成绩只记“合格”与“不合格”,两部分考核都“合格”则该课程考核“合格” 甲、乙、丙三人在理论考核中合格的概率分别为0.9、0.8、0.7;在实验考核中合格的概率分别为0.8、0.7、0.9
甲、乙、丙三人在理论考核中合格的概率分别为0.9、0.8、0.7;在实验考核中合格的概率分别为0.8、0.7、0.9 所有考核是否合格相互之间没有影响
所有考核是否合格相互之间没有影响
(Ⅰ)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
(Ⅱ)求这三人该课程考核都合格的概率(结果保留三位小数)
解:记“甲理论考核合格”为事件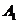 ;“乙理论考核合格”为事件
;“乙理论考核合格”为事件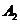 ;“丙理论考核合格”为事件
;“丙理论考核合格”为事件 ;记
;记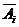 为
为 的对立事件,
的对立事件,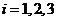 ;记“甲实验考核合格”为事件
;记“甲实验考核合格”为事件 ;“乙实验考核合格”为事件
;“乙实验考核合格”为事件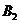 ;“丙实验考核合格”为事件
;“丙实验考核合格”为事件 ;
;
(Ⅰ)记“理论考核中至少有两人合格”为事件 ,记
,记 为
为 的对立事件
的对立事件
解法1: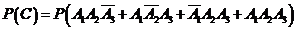


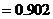
解法2: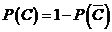
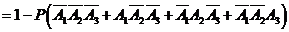
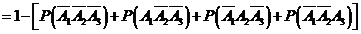
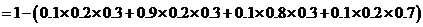
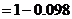
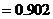
所以,理论考核中至少有两人合格的概率为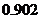
(Ⅱ)记“三人该课程考核都合格” 为事件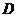

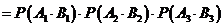
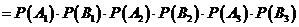
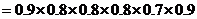

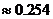
所以,这三人该课程考核都合格的概率为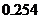
[例4]一个元件能正常工作的概率叫做这个元件的可靠性,设构成系统的每个元件的可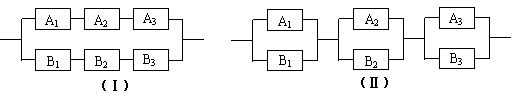 靠性为P(0<P<1,且每个元件能否正常工作是相互独立的。今有6个元件按图所示的两种联接方式构成两个系统(Ⅰ)、(Ⅱ),试分别求出它们的可靠性,并比较它们可靠性的大小。
靠性为P(0<P<1,且每个元件能否正常工作是相互独立的。今有6个元件按图所示的两种联接方式构成两个系统(Ⅰ)、(Ⅱ),试分别求出它们的可靠性,并比较它们可靠性的大小。
解:系统(Ⅰ)有两个道路,它们能正常工作当且仅当两条道路至少有一条能正常工作,而每条
道路能正常工作当且仅当它的每个元件能正常工作。系统(Ⅰ)每条道路正常工作的概率是P3,不能工作的概率是1-P3,系统(Ⅰ)不能工作的概率为(1-P3)2。
故系统(Ⅰ)正常工作的概率是P1=1-(1-P3)2=P3(2-P3);
系统(Ⅱ)有3对并联元件串联而成,它能正常工作,当且仅当每对并联元件都能正常工作,由于每对并联元件不能工作的概率为(1-P)2,因而每对并联元件正常工作的概率是1-(1-P)2, 故系统(Ⅱ)正常工作的概率是:P2=[1-(1-P)2]3=P3(2-P)3。
又P1-P2= P3(2-P3)-P3(2-P)3=-6P3(P-1)2<0,∴P1<P2,故系统(Ⅱ)的可靠性大。
思维点拨:本题的基本思路是从正反两个方面加以分析,先求出每个系统的可靠性再进行比较.
[研讨.欣赏]甲、乙两个乒乓球运动员进行乒乓球比赛,已知每局甲胜的概率为0.6,乙胜的概率为0.4,比赛时可以用三局二胜或五局三胜制,问在哪一种比赛制度下,甲获胜的可能性较大?
解:(1)如果采用三局二胜制,则甲在下列两种情况获胜
A1-2:0(甲净胜两局);A2-2:1(前两局各胜一局,第三局甲胜)
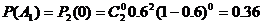
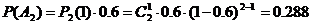
因A1与A2互斥,故甲获胜的概率为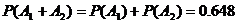
(2)如果采用五局三胜制,则甲在下列三种情况下获胜:
B1-3:0(甲净胜三局);B2-3:1(前三局甲胜两局,负一局,第四局甲胜);B3-3:2(前四局中甲、乙各胜两局,第五局甲胜)
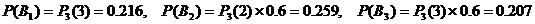 因此甲胜的概率为
因此甲胜的概率为
由(1)、(2)的结果知,甲在五局三胜制中获胜的可能性更大
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com