
5.已知函数f(x)=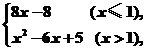 g(x)=lnx,则f(x)与g(x)两函数的图象的交点
g(x)=lnx,则f(x)与g(x)两函数的图象的交点
个数为 ( )
A.1 B.2 C.3 D.4
解析:画出f(x)=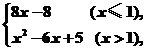
g(x)=lnx的图象如图,两函数的图象的交点个数为3,故选C.
答案:C
|
题组三 |
对数函数的性质 |
4.若函数f(x)=loga(x+b)的图象如图所示,其中a,b为常数,则函数g(x)=ax+b的大致图象是 ( )
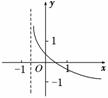
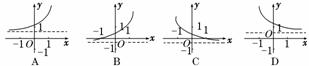
解析:由题意得0<a<1,0<b<1,则函数g(x)=ax+b的大致图象是D.
答案:D
3.(2009·广东高考)若函数y=f(x)是函数y=ax(a>0,且a≠1)的反函数,其图象经过点(,a),则f(x)= ( )
A.log2x B. C.log
C.log x D.x2
x D.x2
解析:由题意f(x)=logax,∴a=logaa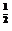 =,
=,
∴f(x)=log x.
x.
答案:C
2.已知log23=a,log37=b,则用a,b表示log1456为 .
解析:∵log23=a,log37=b,∴log27=ab,
∴log1456===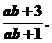
答案: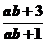
|
题组二 |
对数函数的图象 |
1.设函数f(x)=logax(a>0且a≠1),若f(x1x2…x2010)=8,则f(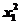 )+f(
)+f(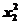 )+…+f(x
)+…+f(x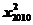 )=( )
)=( )
A.4 B.8 C.16 D.2loga8
解析:∵f(x1x2…x2010)=f(x1)+f(x2)+…+f(2010)=8,
∴f(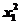 )+f(
)+f(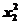 )+…+f(
)+…+f(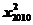 )=2[f(x1)+f(x2)+…+f(x2010)]
)=2[f(x1)+f(x2)+…+f(x2010)]
=2×8=16.
答案:C
21. (本小题满分14分)
已知函数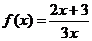 ,数列
,数列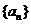 满足
满足 ,
,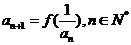 .
.
(1)求数列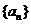 的通项公式;
的通项公式;
(2)令 ,求
,求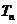 ;
;
(3)令 ,
,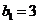 ,
,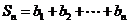 ,若
,若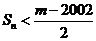 对一切
对一切 成立,求最小正整数m.
成立,求最小正整数m.
19. (本小题满分14分)
A、B两个投资项目的利润率分别为随机变量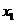 和
和 。根据市场分析,
。根据市场分析,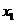 和
和 的分布列分别为:
的分布列分别为:
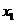 |
5% |
10% |
|
 |
2% |
8% |
12% |
|
P |
0.8 |
0.2 |
|
P |
0.2 |
0.5 |
0.3 |
(1)在A、B两个项目上各投资100万元,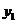 和
和 分别表示投资项目A和B所获得的利润,求方差
分别表示投资项目A和B所获得的利润,求方差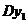 、
、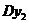 ;
;
(2)将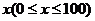 万元投资A项目,
万元投资A项目,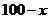 万元投资B项目,
万元投资B项目,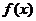 表示投资A项目所得利润的方差与投资B项目所得利润的方差的和. 求
表示投资A项目所得利润的方差与投资B项目所得利润的方差的和. 求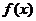 的最小值,并指出x为何值时,
的最小值,并指出x为何值时,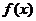 取到最小值.(注:
取到最小值.(注: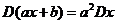 )
)
20(本题满分14分)
椭圆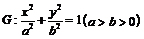 的两个焦点为
的两个焦点为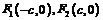 ,M是椭圆上的一点,且满足
,M是椭圆上的一点,且满足
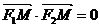 .
.
(1)求离心率的取值范围;
(2)当离心率e取得最小值时,点N(0,3)到椭圆上的点的最远距离为 ;
;
①求此时椭圆G的方程;
②设斜率为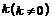 的直线L与椭圆G相交于不同的两点A、B,Q为AB的中点,
的直线L与椭圆G相交于不同的两点A、B,Q为AB的中点,
问A、B两点能否关于过点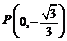 、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
18. (本小题满分14分)
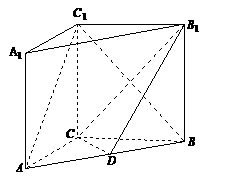 如图,在直三棱柱
如图,在直三棱柱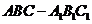 中,AC=3,BC=4,AB=5,
中,AC=3,BC=4,AB=5,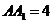 ,点D是AB的中点.
,点D是AB的中点.
(1)求证: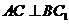 ;
;
(2)求证: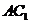 ∥平面
∥平面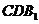 ;
;
(3)求异面直线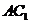 与
与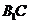 所成角的余弦值.
所成角的余弦值.
17.(本小题满分12分)
设函数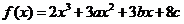 在
在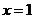 及
及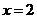 时取极值.
时取极值.
(1)求a、b的值;
(2)若对于任意的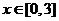 ,都有
,都有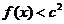 成立,求c的取值范围.
成立,求c的取值范围.
16.(本小题满分12分)
已知函数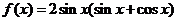 .
.
(1)求函数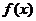 的最小正周期和最大值;
的最小正周期和最大值;
(2)求 在R上的单调区间.
在R上的单调区间.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com