
4、摩擦力
(1)摩擦力的产生;两个相互接触的物体,有相对运动趋势(或相对运动)时产生摩擦力。
(2)作用效果:总是要阻碍物体间的相对运动(或相对运动趋势)。
(3)产生的条件:接触面粗糙;相互接触且挤压;有相对运动(或相对运动趋势)。
(4)摩擦力的方向:总是与物体的相对运动方向(或相对运动趋势方向)相反。
 (5)摩擦力的大小:静摩擦力的大小与外力的变化有关,而与正压力无关,要计算静摩擦力,就需根据物体的运动状态,利用平衡条件或动力学规律来计算求解,其可能的取值范围是0<Ff≤Fm;滑动摩擦力的大小与正压力成正比,即F=μFN,其中的FN表示正压力,不一定等于重力G;μ为动摩擦因数,与接触面的材料和状况有关。
(5)摩擦力的大小:静摩擦力的大小与外力的变化有关,而与正压力无关,要计算静摩擦力,就需根据物体的运动状态,利用平衡条件或动力学规律来计算求解,其可能的取值范围是0<Ff≤Fm;滑动摩擦力的大小与正压力成正比,即F=μFN,其中的FN表示正压力,不一定等于重力G;μ为动摩擦因数,与接触面的材料和状况有关。
例题:如图所示,用跟水平方向成α角的推力F推重量为G的木块沿天花板向右运动,木块和天花板间的动摩擦因数为μ,求木块所受的摩擦力大小。
解析:由竖直方向合力为零可得FN=Fsinα-G,因此有:f =μ(Fsinα-G)
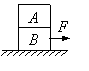 例题:如图所示,A、B为两个相同木块,A、B间最大静摩擦力Fm=5N,水平面光滑。拉力F至少多大,A、B才会相对滑动?
例题:如图所示,A、B为两个相同木块,A、B间最大静摩擦力Fm=5N,水平面光滑。拉力F至少多大,A、B才会相对滑动?
解析:A、B间刚好发生相对滑动时,A、B间的相对运动状态处于一个临界状态,既可以认为发生了相对滑动,摩擦力是滑动摩擦力,其大小等于最大静摩擦力5N,也可以认为还没有发生相对滑动,因此A、B的加速度仍然相等。分别以A和整体为对象,运用牛顿第二定律,可得拉力大小至少为F=10N
(研究物理问题经常会遇到临界状态。物体处于临界状态时,可以认为同时具有两个状态下的所有性质。)
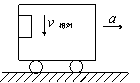 例题: 小车向右做初速为零的匀加速运动,物体恰好沿车后壁匀速下滑。试分析下滑过程中物体所受摩擦力的方向和物体速度方向的关系。
例题: 小车向右做初速为零的匀加速运动,物体恰好沿车后壁匀速下滑。试分析下滑过程中物体所受摩擦力的方向和物体速度方向的关系。
解析:物体受的滑动摩擦力的始终和小车的后壁平行,方向竖直向上,而物体的运动轨迹为抛物线,相对于地面的速度方向不断改变(竖直分速度大小保持不变,水平分速度逐渐增大),所以摩擦力方向和运动方向间的夹角可能取90°和180°间的任意值。
3、弹力
(1)弹力的产生:发生弹性形变的物体,由于要恢复原来的形状,对跟它接触的物体产生力的作用,这种力叫弹力。
(2)产生的条件:两物体要相互接触;发生弹性形变。
(3)弹力的方向:①压力、支持力的方向总是垂直于接触面。
②绳对物体的拉力总是沿着绳收缩的方向。
③杆对物体的弹力不一定沿杆的方向。如果轻直杆只有两个端点受力而处于平衡状态,则轻杆两端对物体的弹力的方向一定沿杆的方向。
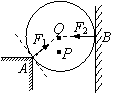 例题:如图所示,光滑但质量分布不均的小球的球心在O,重心在P,静止在竖直墙和桌边之间。试画出小球所受弹力。
例题:如图所示,光滑但质量分布不均的小球的球心在O,重心在P,静止在竖直墙和桌边之间。试画出小球所受弹力。
解析:由于弹力的方向总是垂直于接触面,在A点,弹力F1应该垂直于球面所以沿半径方向指向球心O;在B点弹力F2垂直于墙面,因此也沿半径指向球心O。
注意弹力必须指向球心,而不一定指向重心。又由于F1、F2、G为共点力,重力的作用线必须经过O点,因此P和O必在同一竖直线上,P点可能在O的正上方(不稳定平衡),也可能在O的正下方(稳定平衡)。
 例题: 如图所示,重力不可忽略的均匀杆被细绳拉住而静止,试画出杆所受的弹力。
例题: 如图所示,重力不可忽略的均匀杆被细绳拉住而静止,试画出杆所受的弹力。
解析:A端所受绳的拉力F1沿绳收缩的方向,因此沿绳向斜上方;B端所受的弹力F2垂直于水平面竖直向上。
由于此直杆的重力不可忽略,其两端受的力可能不沿杆的方向。
 杆受的水平方向合力应该为零。由于杆的重力G竖直向下,因此杆的下端一定还受到向右的摩擦力f作用。
杆受的水平方向合力应该为零。由于杆的重力G竖直向下,因此杆的下端一定还受到向右的摩擦力f作用。
例题: 图中AC为竖直墙面,AB为均匀横梁,其重为G,处于水平位置。BC为支持横梁的轻杆,A、 B、C三处均用铰链连接。试画出横梁B端所受弹力的方向。
解析:轻杆BC只有两端受力,所以B端所受压力沿杆向斜下方,其反作用力轻杆对横梁的弹力F沿轻杆延长线方向斜向上方。
(4)弹力的大小:对有明显形变的弹簧、橡皮条等物体,弹力的大小可以由胡克定律计算。对没有明显形变的物体,如桌面、绳子等物体,弹力大小由物体的受力情况和运动情况共同决定,根据运动情况,利用平衡条件或动力学规律来计算。
胡克定律:在弹性限度内,弹簧的弹力与弹簧的伸长(或收缩)的长度x成正比,F=kx,k是劲度系数。除此之外,一般物体的弹力大小,就需
例题:如图所示,两物体重分别为G1、G2,两弹簧劲度分别为k1、k2,弹簧两端与物体和地面相连。用竖直向上的力缓慢向上拉G2,最后平衡时拉力F=G1+2G2,求该过程系统重力势能的增量。
 解析:关键是搞清两个物体高度的增量Δh1和Δh2跟初、末状态两根弹簧的形变量Δx1、Δx2、Δx1/、Δx2/间的关系。
解析:关键是搞清两个物体高度的增量Δh1和Δh2跟初、末状态两根弹簧的形变量Δx1、Δx2、Δx1/、Δx2/间的关系。
无拉力F时 Δx1=(G1+G2)/k1,Δx2= G2/k2,(Δx1、Δx2为压缩量)
加拉力F时 Δx1/=G2/k1,Δx2/= (G1+G2) /k2,(Δx1/、Δx2/为伸长量)
而Δh1=Δx1+Δx1/,Δh2=(Δx1/+Δx2/)+(Δx1+Δx2)
系统重力势能的增量ΔEp= G1žΔh1+G2žΔh2
整理后可得: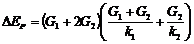
2、重力:由于地球吸引,而使物体受到的力。
(1)重力的产生:由于地球的吸引而使物体受到的力叫重力。
(2)重力的大小:G=mg,可以用弹簧秤测量,重力的大小与物体的速度、加速度无关。
(3)重力的方向:竖直向下。
(4)重心:重力的作用点。重心的测定方法:悬挂法。重心的位置与物体形状的关系:质量分布均匀的物体,重心位置只与物体形状有关,其几何中心就是重心;质量分布不均匀的物体,其重心的位置除了跟形状有关外,还跟物体的质量分布有关。
1、力:力是物体对物体的作用。
⑴力是一种作用,可以通过直接接触实现(如弹力、摩擦力),也可以通过场来实现(重力、电场力、磁场力)
⑵力的性质:物质性(力不能脱离物体而独立存在);相互性(成对出现,遵循牛顿第三定律);矢量性(有大小和方向,遵从矢量运算法则);效果性(形变、改变物体运动状态,即产生加速度)
⑶力的要素:力的大小、方向和作用点称为力的三要素,它们共同影响力的作用效果。
力的描述:描述一个力,应描述力的三要素,除直接说明外,可以用力的图示和力的示意图的方法。
⑷力的分类:按作用方式,可分为场力(重力、电场力)、接触力(弹力、摩擦力);接效果分,有动力、阻力、牵引力、向心力、恢复力等;接性质分,有重力、弹力、摩擦力、分子力等;按研究系统分,内力、外力。
4.(本小题满分10分)一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数:f1(x)=x,f2(x)=x2,f3(x)=x3,f4(x)=sinx,f5(x)=cosx,f6(x)=2.
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数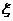 的分布列和数学期望.
的分布列和数学期望.
3.把下列参数方程化为普通方程,并说明它们各表示什么曲线。
(1)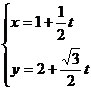 (t为参数);
(t为参数);
(2)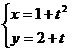 (t为参数);
(t为参数);
2.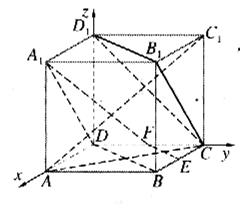 已知E,F分别是正方体ABCD-A1B1C1D1的棱BC和CD的中点,求:
已知E,F分别是正方体ABCD-A1B1C1D1的棱BC和CD的中点,求:
(1)A1D与EF所成角的大小;
(2)A1F与平面B1EB所成角;
(3)二面角C-D1B1-B的大小.
1.设n为大于1的自然数,求证: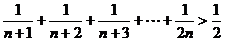 .
.
20.(本题满分16分)
已知函数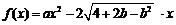 ,
, .
.
(1)当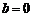 时,若
时,若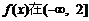 上单调递减,求a的取值范围;
上单调递减,求a的取值范围;
(2)求满足下列条件的所有整数对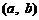 :存在
:存在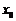 ,使得
,使得 的最大值,
的最大值, 的最小值;
的最小值;
(3)对满足(II)中的条件的整数对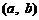 ,试构造一个定义在
,试构造一个定义在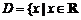 且
且 上的函数
上的函数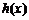 :使
:使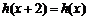 ,且当
,且当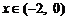 时,
时, .
.
附加题
19.(本小题满分16分)
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点。已知AB=3米,AD=2米。
(I)设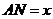 (单位:米),要使花坛AMPN的面积大于32平方米,求
(单位:米),要使花坛AMPN的面积大于32平方米,求 的取值范围;
的取值范围;
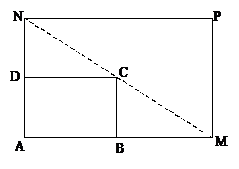 (II)若
(II)若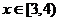 (单位:米),则当AM,AN的长度分别是多少时,花坛AMPN的面积最大?并求出最大面积。
(单位:米),则当AM,AN的长度分别是多少时,花坛AMPN的面积最大?并求出最大面积。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com