
6、超导现象
(1)超导现象:某些物质当温度降到一定程度时,电阻突然降为零的现象,称为超导现象。
(2)超导体:能够发生超导现象的物质,称为超导体。
(3)转变温度:导体由普通状态向超导态转变时的温度称为超导转变温度,或临界温度。用TC表示。
|
物质 |
临界温度t/K |
物质 |
临界温度t/K |
|
钨(W) |
0.012 |
镤(Pa) |
1.4 |
|
铪(Hf) |
0.134 |
铊(Tl) |
2.39 |
|
铱(Ir) |
0.140 |
铟(In) |
3.4035 |
|
钛(Ti) |
0.39 |
锡(Sn) |
3.722 |
|
钌(Ru) |
0.49 |
汞(Hg) |
4.153 |
|
锆(Zr) |
0.546 |
钽(Ta) |
4.4831 |
|
镉(Cd) |
0.56 |
镧(La) |
4.92 |
|
锇(Os) |
0.655 |
钒(V) |
5.30 |
|
铀(U) |
0.68 |
铅(Pb) |
7.193 |
|
锌(Zn) |
0.75 |
锝(Tc) |
8.22 |
|
钼(Mo) |
0.92 |
铌(Nb) |
9.25 |
|
镓(Ga) |
1.091 |
铌三铝(Nb3AL) |
17.2 |
|
铝(Al) |
1.196 |
铌三锗(Nb3Ge) |
22.5 |
|
钍(Th) |
1.368 |
铌三锡(Nb3Sn) |
18 |
5、半导体的导电特性
(1)半导体的热敏特性:半导体材料的电阻随温度升高而减小,称为半导体的热敏特性。
(2)半导体的光敏特性:半导体材料的电阻随光照而减小,称为半导体的光敏特性。
(3)半导体的掺杂特性:在纯净的半导体材料中掺入微量的杂质,会使它的电阻急剧变化,半导体的导电性能大大增强,称为半导体的掺杂特性。
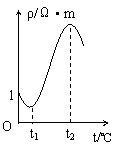 例题:家用电热灭蚊器中电热部分的主要部件是PTC元件,PTC元件是由酞酸钡等半导体材料制成的电阻器,其电阻率与温度的关系如图4所示,由于这种特性,PTC元件具有发热、控温两重功能,对此以下说法中正确的是( )
例题:家用电热灭蚊器中电热部分的主要部件是PTC元件,PTC元件是由酞酸钡等半导体材料制成的电阻器,其电阻率与温度的关系如图4所示,由于这种特性,PTC元件具有发热、控温两重功能,对此以下说法中正确的是( )
A.通电后其功率先增大后减小
B.通电后其功率先减小后增大
C.当其产生的热量与散发的热量相等时,温度保持在t1至t2的某一值不变
D.当其产生的热量与散发的热量相等时,温度保持在t1或t2不变
解析:根据PTC元件的电阻率随温度变化的曲线,可知在常温下,它的电阻是相当小的,通入电流以后,随着温度的升高,其电阻率先变小后增大,那么它的功率先变大,后变小,温度保持在在t1至t2的某一值不变,这时候电路处于稳定状态,如果温度再升高,电阻率变大,导致电流变小,温度就会降下来;如果温度降低,电阻率减小,导致电流变大,温度就会升上去,所以本题正确答案为:A、C。
例题:一般的电熨斗用合金丝作发热元件,合金丝电阻R随温度t变化的关系如图5所示的实线①,由于环境温度、熨烫衣服的厚度、干湿等情况不同,熨斗的散热功率不同,因而熨斗的温度可能会在较大的范围内波动,易损坏衣服。
有一种用主要成份为BaTiO3的称为“PTC”的特殊材料作发热元件的电熨斗,具有升温快,能自动控制温度的特点,PTC材料的电阻随温度变化的关系如图中实线②所示。
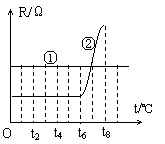 (1)为什么原处于冷态的“PTC”熨斗刚通电时,比普通电熨斗升温快?
(1)为什么原处于冷态的“PTC”熨斗刚通电时,比普通电熨斗升温快?
(2)通电一段时间后,电熨斗温度稳定在什么范围内?
(3)简析PTC发热元件的自动控温过程。
解析:解答此题的关键是要看懂图中涉及的物理量的含义:图线①说明合金的电阻基本上不随温度的变化而变化;图线②说明在较低的温度下,“PTC”材料的电阻基本不变,但在某一温度范围内电阻会突变。
 (1) 由图可知,冷态的“PTC”材料的电熨斗电阻比一般电熨斗电阻小,所以发热功率P=U2/R较一般电熨斗大,所以在相同的时间内“PTC”升温快。
(1) 由图可知,冷态的“PTC”材料的电熨斗电阻比一般电熨斗电阻小,所以发热功率P=U2/R较一般电熨斗大,所以在相同的时间内“PTC”升温快。
(2)由图可知,温度自动稳定在t6<t<t8范围内。
(3 )当熨斗温度升高到t6后,“PTC”材料的电阻急剧增大,电功率变小,此时如果散热功率大于电功率,熨斗温度会下降,当温度降低时,电阻R急剧减小,电功率增大,温度又升高……,因而熨斗的温度能稳定在一定的范围内。
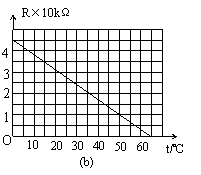
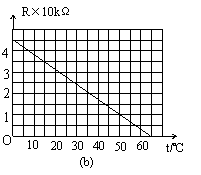 例题:如图所示,为在温度为10℃左右的环境中工作的某自动恒温箱原理简图。箱内的电阻R1=20kΩ,R,2=10kΩ,R3=40kΩ,Rt为热敏电阻,它的电阻随温度的变化的图线如图7(b)所示,当a、b两端电压Uab<0时,电压鉴别器会令开关K接通,恒温箱内的电热丝发热,使箱内温度提高,当Uab>0时,电压鉴别器会K断开,停止加热,恒温箱内的温度恒定在多少摄氏度。
例题:如图所示,为在温度为10℃左右的环境中工作的某自动恒温箱原理简图。箱内的电阻R1=20kΩ,R,2=10kΩ,R3=40kΩ,Rt为热敏电阻,它的电阻随温度的变化的图线如图7(b)所示,当a、b两端电压Uab<0时,电压鉴别器会令开关K接通,恒温箱内的电热丝发热,使箱内温度提高,当Uab>0时,电压鉴别器会K断开,停止加热,恒温箱内的温度恒定在多少摄氏度。
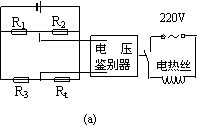
解析:在Uab<0时,K接通,箱内的温度提高,导致Rt减小。当Rt=20kΩ时达到电桥平衡,此时Uab=0,而Uab=0是K断开、闭合的分界点,故此温度可由图7(b)中读出,Rt=20kΩ时对应的温度t=35℃。
4、半导体
(1)半导体
导电性能介于导体和绝缘体之间,而且电阻不随温度的增加而增加,反随温度的增加而减小,这种材料称为半导体。
(2)从电阻率的观点认识导体、绝缘体、半导体
金属导体的电阻率约为10-8-10-6Ω·m
绝缘体的电阻率约为108-1018Ω·m
半导体的电阻率介于导体和绝缘体之间,约为10-5-106Ω·m
4、电流的微观表达式
(1)三种速率
①热运动的平均速率:金属导体中的大量自由电子在不停地做无规则热运动,热运动的平均速率很大,但从其宏观效果上看,没有电荷的定向移动,因而热运动的平均速率对形成电流没有贡献。
②定向移动的平均速率:导体中自由电荷定向移动的平均速率是很小的,但就是这一定向移动的速率使电荷定向移动形成了电流。
③电场传播速率:电场的传播速率等于真空中的光速,电路一接通,导体中民光速的速率在各处建立电场,导体中各处的自由电荷几乎同时开始做定向移动,整个电路几乎同时形成电流。
(2)电流的微观表达式
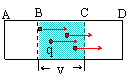 如图所示,AD表示粗细均匀的一段导体,两端加以一定的电压。
如图所示,AD表示粗细均匀的一段导体,两端加以一定的电压。
设导体中的自由电荷沿导体定向移动的速率为v,导体的横截面积为S,导体中每单位体积的自由数为n,每个自由电荷所带的电荷量为q。
①导体中单位时间内能够通过截面C的自由电荷分布
导体中单位时间内能够通过截面C的自由电荷分布在以截面C为底,速率v为长的导体中。
②单位时间内能够通过截面C的自由电荷数
N=nV=nvS
③单位时间内能够通过截面C的电荷量
Q=Nq=nqvS
④电流的微观表达式
I==nqvS
3、导体的伏安特性
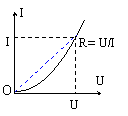
(1) 导体的伏安特性曲线
①导体的伏安特性曲线
 用纵轴表示电流I,用横轴表示电压U,画出的I-U图线叫做导体的伏安特性曲线。
用纵轴表示电流I,用横轴表示电压U,画出的I-U图线叫做导体的伏安特性曲线。
如下图所示,是金属导体的伏安特性曲线。
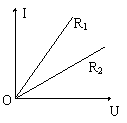
②图线斜率的物理意义
在I-U图中,图线的斜率表示导体电阻的倒数。
即k=tanθ==
 图线的斜率越大,电阻越小。右图中R1<R2。
图线的斜率越大,电阻越小。右图中R1<R2。
③线性元件和非线性元件
a.线性元件:伏安特性曲线是过坐标原点的直线,这样的元件叫线性元件。
b.非线性元件:伏安特性曲线不是直线,这样的元件叫非线性元件。
注意:欧姆定律不适用的导体和器件,电流和电压不成正比,伏安特性曲线不是直线,都是非线性元件。
1、电流
(1)概念:电荷的定向移动形成电流。
(2)产生电流的条件
①内因:要有能够自由移动的电荷──自由电荷。
②外因:导体两端存在电压──在导体内建立电场。
干电池、蓄电池、发电机等都是电源,它们的作用是提供并保持导体的两端的电压,使导体中有持续的电流。
(3)电流的方向:正电荷的定向移动方向为电流方向。
总结:在金属导体中,电流的方向与自由电子定向移动的方向相反。在电解质溶液中,电流的方向与正离子定向移动的方向相同,与负离子定向移动的方向相反。
(4)电流
①定义:通过导体横截面的电荷量q跟通过这些电荷量所用的时间t的比值称为电流。
②公式:I= (量度式)
③单位:在国际单位制中,电流的单位是安培,简称安,符号是A。
电流的常用单位还有毫安(mA)和微安(μA),它们之间的关系是:
1 mA=10-3A
1μA=10-6A
④测量仪器
在实际中,测量电流的仪器是电流表。
(5)直流与恒定电流
①直流:方向不随时间而改变的电流叫做直流。
②恒定电流:方向和强弱都不随时间而改变的电流叫做恒定电流。
例题:关于电流的方向,下列叙述中正确的是( )
A.金属导体中电流的方向就是自由电子定向移动的方向
B.在电解质溶液中有自由的正离子和负离子,电流方向不能确定
C.不论何种导体,电流的方向规定为正电荷定向移动的方向
D.电流的方向有时与正电荷定向移动的方向相同,有时与负电荷定向移动的方向相同.
解析:正确选项为C。
电流是有方向的,电流的方向是人为规定的.物理上规定正电荷定向移动的方向为电流的方向,则负电荷定向移动的方向一定与电流的方向相反.
例题:某电解质溶液,如果在1 s内共有5.0×1018个二价正离子和1.0×1019个一价负离子通过某横截面,那么通过电解质溶液的电流强度是多大?
解析:设在t=1 s内,通过某横截面的二价正离子数为n1,一价离子数为n2,元电荷的电荷量为e,则t时间内通过该横截面的电荷量为q=(2n1+N2)e,所以电流为
I==3.2 A。
例题:氢原子的核外只有一个电子,设电子在离原子核距离为R的圆轨道上做匀速圆周运动.已知电子的电荷量为e,运动速率为v,求电子绕核运动的等效电流多大?
解析:取电子运动轨道上任一截面,在电子运动一周的时间T内,通过这个截面的电量q=e,由圆周运动的知识有:T=
根据电流的定义式得:I==
例题:来自质子源的质子(初速度为零),经一加速电压为800kV的直线加速器加速,形成电流强度为1mA的细柱形质子流。已知质子电荷e=1.60×10-19C。这束质子流每秒打到靶上的质子数为_________。假定分布在质子源到靶之间的加速电场是均匀的,在质子束中与质子源相距L和4L的两处,各取一段极短的相等长度的质子流,其中的质子数分别为n1和n2,则n1∶n2=_______。
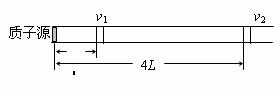
解:按定义,
由于各处电流相同,设这段长度为l,其中的质子数为n个,
则由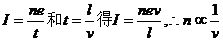 。而
。而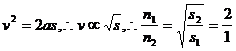
(四)、透镜:
⑴透镜:是利用光的折射控制光路和成像的光学器材。
①透镜:是两个表面分别为球面(或一面为球面,另一面为平面)的透明体。
凸透镜:中间厚边缘薄的透镜。
凹透镜:中间薄边缘厚的透镜。
②透镜的光心、主轴、焦点和焦距的概念(略)。
③本节研究的内容适用薄透镜、近轴光线。
⑵透镜对光线的作用
凸透镜:对光线有会聚作用。
凹透镜:对光线有发散作用。
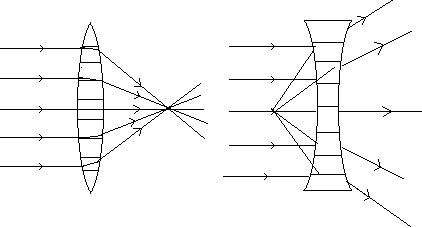
注意理解:
①透镜对光线的作用,是通过两次折射来实现的。
②从凸透镜射出的光线不一定是会聚光束。
从凹透镜射出的光线也不一定是发散光束。
⑶透镜成像规律:
①规律:
|
透镜 |
物的位置 |
像的位置 |
像的性质 |
像的下倒 |
像的大小 |
  |
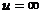 |
异侧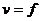 |
实像点 |
|
|
|
凸 |
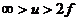 |
异侧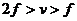 |
实像 |
倒立 |
缩小 |
|
透 |
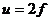 |
异侧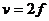 |
实像 |
倒立 |
等大 |
|
镜 |
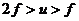 |
异侧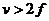 |
实像 |
倒立 |
放大 |
|
|
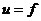 |
不 成 像 |
|||
|
|
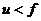 |
同侧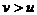 |
虚像 |
正立 |
放大 |
|
凹 透 镜 |
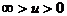 |
同侧  |
虚像 |
正立 |
缩小 |
②实像和虚像比较:
|
|
实像 |
虚像 |
|
形成 |
由射出光学元件的光线实际会聚而成 |
由射出光学元件的光线的反向沿长线会聚而成 |
|
观察 |
可成在光屏上,也可用眼睛直接看 |
只能用眼睛直接看不能成在光屏上 |
⑷透镜成像公式:
①公式: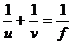
符号:物距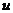 :取“+”。
:取“+”。
像距v:实像取“+”;虚像取“-”。
焦距f:凸透镜取“+”;凹透镜取“-”。
②放大率(m):
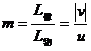
⑸透镜成像光路作图。
①三条基本光线。
a. 平行主轴的光线,经透镜折射后,出射光线过焦点。
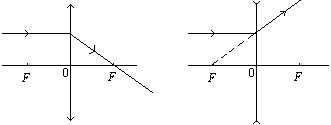
b.过焦点的光线,经透镜折射后平行主轴。
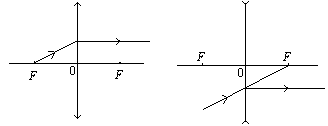
c.过光心的光线,经透镜后不改变方向。
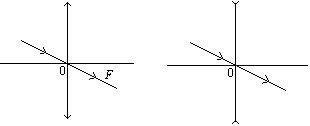
②透镜成像作用:
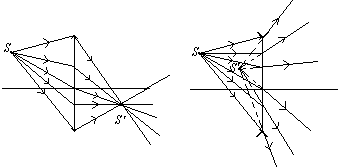
成像是光源s发出的光线经透镜折射后会聚于一点(或反向沿长线会聚于一点)。
在所有光线中选择两条基本光线可以确定像的位置。
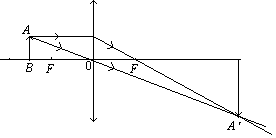
(三)棱镜:
⑴棱镜的色散:
①棱镜对一束单色兴的作用:
一束光从空气,射向棱镜的一侧面时,经过两次折射,出射光相对入射光方向偏折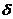 角,出射光偏向底边。
角,出射光偏向底边。
②棱镜对白光的色散作用:
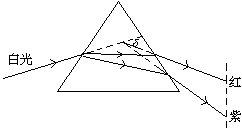
a.现象:白光通过三棱镜后被分解成不同的色光。并按顺序排列为红、橙、黄、绿、蓝、靛、紫。这种现象称色散现象。
b.说明:①白光是复色光,由不同颜色 的单色光组成。
②各种色光的偏折角度不同,所 以介质对不同色光的折射率 不同。由于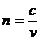 所以各种色 光在同一介质中的传播速度不同。
所以各种色 光在同一介质中的传播速度不同。
如图对红光偏折角最小;对红光折射率最小;红光在玻璃中传播速度最大。
对紫光偏折角最大;对紫光折射率最大;紫光在玻璃中传播速度最小。
⑵全反射棱镜:
全反射棱镜,为横截面是等腰直角三角形的棱镜它可以将光全部反射,常用来控制光路。

例题:如图所示,一细束红光和一细束蓝光平行射到同一个三棱镜上,经折射后交于光屏上的同一个点M,若用n1和n2分别表示三棱镜对红光和蓝光的折射率,下列说法中正确的是
A.n1<n2,a为红光,b为蓝光 B.n1<n2,a为蓝光,b为红光
C.n1>n2,a为红光,b为蓝光 D.n1>n2,a为蓝光,b为红光
解析:由图可知,b光线经过三棱镜后的偏折角较小,因此折射率较小,是红光。
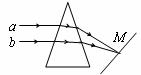
例题:如图所示,两细束平行的单色光a、b射向同一块玻璃砖的上表面,最终都从玻璃砖的下表面射出。已知玻璃对单色光a的折射率较小,那么下列说法中正确的有
A.进入玻璃砖后两束光仍然是平行的
B.从玻璃砖下表面射出后,两束光不再平行
C.从玻璃砖下表面射出后,两束光之间的距离一定减小了
D.从玻璃砖下表面射出后,两束光之间的距离可能和射入前相同
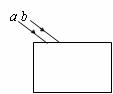
解析:进入时入射角相同,折射率不同,因此折射角不同,两束光在玻璃内不再平行,但从下表面射出时仍是平行的。射出时两束光之间的距离根据玻璃砖的厚度不同而不同,在厚度从小到搭变化时,该距离先减小后增大,有可能和入射前相同(但左右关系一定改变了)。
例题: 如图所示,一束平行单色光a垂直射向横截面为等边三角形的棱镜的左侧面,棱镜材料的折射率是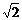 。试画出该入射光射向棱镜后所有可能的射出光线。
。试画出该入射光射向棱镜后所有可能的射出光线。
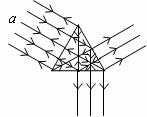
解析:由折射率为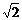 得全反射临界角是45°。光线从左侧面射入后方向不发生改变,射到右侧面和底面的光线的入射角都是60°,大于临界角,因此发生全反射。反射光线分别垂直射向底面和右侧面。在底面和右侧面同时还有反射光线。由光路可逆知,它们最终又从左侧面射出。所有可能射出的光线如图所示。
得全反射临界角是45°。光线从左侧面射入后方向不发生改变,射到右侧面和底面的光线的入射角都是60°,大于临界角,因此发生全反射。反射光线分别垂直射向底面和右侧面。在底面和右侧面同时还有反射光线。由光路可逆知,它们最终又从左侧面射出。所有可能射出的光线如图所示。
(二)全反射:
⑴全反射现象:
①光从光密介质射入光疏介质时,折射角大于入射角,当入射角增大到某一角度时,折射光消失,只剩下反射光,光全部被反射回光密介质中,这种现象叫全反射。
②增大入射角时,不但折射角和反射角增大,光的强度也在变化,即折射光越来越弱;反射光越来越强;全反射时,入射光能量全部反射回到原来的介质中。
⑵临界角(A):
定义:当光从某种介质射向真空时,折射角度为90°时的入射角叫做临界角。
用A表示。根据折射定律:
⑶发生全反射的条件:
①光从光密介质入射光疏介质。
②入射角大于临界角。
⑷光导纤维
全反射的一个重要应用就是用于光导纤维(简称光纤)。光纤有内、外两层材料,其中内层是光密介质,外层是光疏介质。光在光纤中传播时,每次射到内、外两层材料的界面,都要求入射角大于临界角,从而发生全反射。这样使从一个端面入射的光,经过多次全反射能够没有损失地全部从另一个端面射出。
例题:如图所示,一条长度为L=5.0m的光导纤维用折射率为n=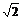 的材料制成。一细束激光由其左端的中心点以α= 45°的入射角射入光导纤维内,经过一系列全反射后从右端射出。求:⑴该激光在光导纤维中的速度v是多大?⑵该激光在光导纤维中传输所经历的时间是多少?
的材料制成。一细束激光由其左端的中心点以α= 45°的入射角射入光导纤维内,经过一系列全反射后从右端射出。求:⑴该激光在光导纤维中的速度v是多大?⑵该激光在光导纤维中传输所经历的时间是多少?

解析:⑴由n=c/v可得v=2.1×108m/s
⑵由n=sinα/sinr可得光线从左端面射入后的折射角为30°,射到侧面时的入射角为60°,大于临界角45°,因此发生全反射,同理光线每次在侧面都将发生全反射,直到光线达到右端面。由三角关系可以求出光线在光纤中通过的总路程为s=2L/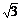 ,因此该激光在光导纤维中传输所经历的时间是t=s/v=2.7×10-8s。
,因此该激光在光导纤维中传输所经历的时间是t=s/v=2.7×10-8s。
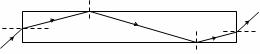
例题:如图所示,自行车的尾灯采用了全反射棱镜的原理。它虽然本身不发光,但在夜间骑行时,从后面开来的汽车发出的强光照到尾灯后,会有较强的光被反射回去,使汽车司机注意到前面有自行车。尾灯的原理如图所示,下面说法中正确的是
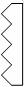
A.汽车灯光应从左面射过来在尾灯的左表面发生全反射
B.汽车灯光应从左面射过来在尾灯的右表面发生全反射
C.汽车灯光应从右面射过来在尾灯的左表面发生全反射
D.汽车灯光应从右面射过来在尾灯的右表面发生全反射
解析:利用全反射棱镜使入射光线偏折180°,光线应该从斜边入射,在两个直角边上连续发生两次全反射。所以选C。
例题:如图所示,AB为一块透明的光学材料左侧的端面。建立直角坐标系如图,设该光学材料的折射率沿y轴正方向均匀减小。现有一束单色光a从原点O以某一入射角θ由空气射入该材料内部,则该光线在该材料内部可能的光路是下图中的哪一个
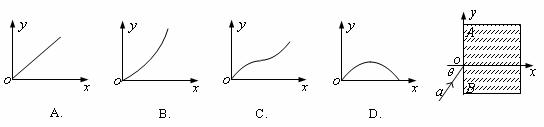
解析:如图所示,由于该材料折射率由下向上均匀减小,可以设想将它分割成折射率不同的薄层。光线射到相邻两层的界面时,如果入射角小于临界角,则射入上一层后折射角大于入射角,光线偏离法线。到达更上层的界面时入射角逐渐增大,当入射角达到临界角时发生全反射,光线开始向下射去直到从该材料中射出。
例题:如图所示,用透明材料做成一长方体形的光学器材,要求从上表面射入的光线可能从右侧面射出,那么所选的材料的折射率应满足
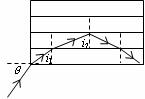
A.折射率必须大于 B.折射率必须小于
B.折射率必须小于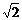
C.折射率可取大于1的任意值 D.无论折射率是多大都不可能
解析:从图中可以看出,为使上表面射入的光线经两次折射后从右侧面射出,θ1和θ2都必须小于临界角C,即θ1<C,θ2<C,而θ1+θ2=90°,故C>45°,n=1/sinC<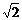 ,选B答案。
,选B答案。

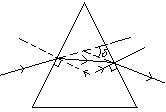
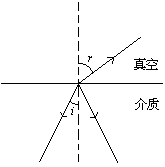
(一)、折射定律:
⑴折射现象:
光从一种介质,斜射入另一种介质的界面时,其中一部分光进另一种介质中传播,并且改变了传播方向:这种现象叫折射观察(光由一种介质,垂直界面方向入射另一种介质时传播方向不发生改变)。
⑵折射定律:

⑶折射率(n):

①定义:光从真空射入某介质时,入射角正弦和折射角正弦的比,称为该介质的折射率。用n表示。
即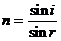
②折射率反映了介质对光的折射能力。如图光从真空以相同的入射角i,入射不同介质时,n越大,根据折射定律,折射角r越小,则偏折角 越大。
越大。
③折射率和光在该介质中传播速度有关。
a.折射率等于光在真空中速度c,与光在介质中速度 之比。
之比。
即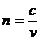
b.由于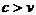 。所以
。所以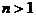
④光疏介质和光密介质:
光疏介质:折射率小的介质叫光疏介质。在光疏介质中,光速较大。
光密介质:折射率大的介质叫光密介质在光密介质中,光速较小。
4、反射和折射现象中,光路可逆。
例题: 直角三棱镜的顶角α=15°, 棱镜材料的折射率n=1.5,一细束单色光如图所示垂直于左侧面射入,试用作图法求出该入射光第一次从棱镜中射出的光线。
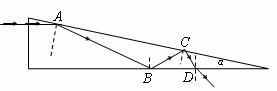
 解析:由n=1.5知临界角大于30°小于45°,边画边算可知该光线在射到A、B、C、D各点时的入射角依次是75°、60°、45°、30°,因此在A、B、C均发生全反射,到D点入射角才第一次小于临界角,所以才第一次有光线从棱镜射出。
解析:由n=1.5知临界角大于30°小于45°,边画边算可知该光线在射到A、B、C、D各点时的入射角依次是75°、60°、45°、30°,因此在A、B、C均发生全反射,到D点入射角才第一次小于临界角,所以才第一次有光线从棱镜射出。
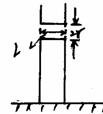
例题:为了观察门外情况,有人在门上开一小圆孔,将一块圆柱形玻璃嵌入其中,圆柱体轴线与门面垂直,如图所示.从圆柱底面中心看出去,可以看到的门外入射光线与轴线间的最大夹角称做视场角.已知该玻璃的折射率为n,圆柱深为l,底面半径为r.则视场角是( )
??A、arcsin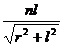 B、arcsin
B、arcsin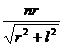
??C、arcsin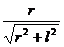 ??????D、arcsin
??????D、arcsin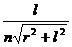
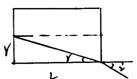 解析:如图所示,当门外的入射光线进入玻璃时,
解析:如图所示,当门外的入射光线进入玻璃时,
光线会发生折射现象,且入射角大于折射角,所以
观察者的视场范围变大,人的视角较小。由图可知:
sini=nsinr=n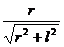 。
。
∴i=arcsin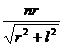
所以本题的答案是B。
例题:已知一束单色光在水中的传播速度是真空中的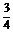 ,则( )
,则( )
A.这束光在水中传播时的波长为真空中的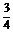
B.这束光在水中传播时的频率为真空中的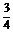
C.对于这束光,水的折射率为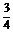
D.从水中射向水面的光线,一定可以进入空气中
解析: 由题意可知,当光从一种介质进入另一种介质时,光的频率是不变的。所以当光从水中进入空气中,频率不变,而传播速度变大,即波长也相应变大,波长为原波长的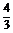 倍,n=
倍,n=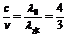 ,λ
,λ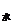 =
=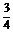 λ。当光从水中进入空气中,即从光密介质进入光疏介质,如入射角大于临界角就会发生全反射,无光线进入空气中。
λ。当光从水中进入空气中,即从光密介质进入光疏介质,如入射角大于临界角就会发生全反射,无光线进入空气中。
即正确答案为A。
例题:已知介质对某单色光的临界角为θ,则( ).
A.该介质对此单色光的折射率等于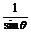
B.此单色光在该介质中的传播速度等于csinθ倍(c是真空中的光速)
C.此单色光在该介质中的波长是在真空中的波长的sinθ倍
D.此单色光在该介质中的频率是在真空中频率的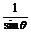 倍
倍
解析:由临界角的计算公式可知:sinθ=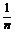 ,得n=
,得n=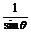 ,故A对.光在介质中的传播速度v=
,故A对.光在介质中的传播速度v=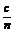 =c·sinθ,故B对.此单色光在介质中的波长λ=
=c·sinθ,故B对.此单色光在介质中的波长λ=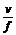 ,又因为c=λ
,又因为c=λ f,得f =
f,得f =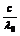 ,
,
即可得:λ=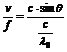 λ
λ ·sinθ.λ
·sinθ.λ 为该光在真空中的波长,所以C正确.因为光从一种介质进入另一种介质时频率不变,且等于在真空中的频率,所以D错。
为该光在真空中的波长,所以C正确.因为光从一种介质进入另一种介质时频率不变,且等于在真空中的频率,所以D错。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com