
1、电荷守恒定律
电荷既不能创造,也不能消灭,只能从一个物体转移到另一个物体,或者从物体的一部分转移到另一部分,在转移的过程中,电荷的总量不变,这个结论叫做电荷守恒定律。
形状完全相同的两个小球
(1)若一个带电,一个不带电,两小球接触后再分开,则电荷量平分.
(2)若两小球分别带同种电荷q1、q2,两者接触后再分开,则每个小球带电为.
(3)若两小球分别带异种电荷q1、q2,两者接触后再分开,则每个小球带电为.
18、常用电容器
电容器从构造上看,分固定电容器和可变电容器。
(1)固定电容器
固定电容器的电容是固定不变的。
(2)可变电容器
可变电容器的电容是可以改变的。
(3)电容器的两个重要参数
①电容值
②击穿电压:加在电容器两极上的电压超过某一值(击穿电压)时,板间电介质被击穿,电容器将被损坏,这个极限电压称为击穿电压。
额定电压:指电容器长期工人作时所能承受的电压,额定电压应小于击穿电压,电容器工作时的电压不应超过额定值。

17、平行板电容器的电容
(1)平行板电容器:两块平行且相互绝缘的金属板构成的电容器,叫做平行板电容器。
平行板电容器是电容器中具有代表性的一种。可描述一对平行板的几何特性,强调一下:①两极间距d;②两极板的正对面积S。
⑵介绍静电计:静电计是在电容器的基础上制成的,用来测量电势差。把它的金属球接一导体,金属外壳接另一导体,从指针的偏角可测出两导体间的电势差,指针偏角越大,指针与外壳间电势差越大。
⑶跟平行板电容器的电容有关的因素
①与极板间的距离有关
d↑→C↓,d↓→C↑
②与极板的正对面积有关
S↑→C↑,S↓→C↓
③与极板间的介质有关
板间充满某种介质时,C会变为板间为真空时的若干倍。
⑷平行板电容器电容的决定公式
C= (决定式)
注意:①平行板电容器充电后保持两极板与电源相连,U、C、Q、E怎样随d、S变化
U不变,等于电源电压。
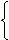 C↓→Q↓
C↓→Q↓
d↑→
E(=U/d)↓
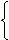 C↑→Q↑
C↑→Q↑
S↑→
E(=U/d)不变
②平行板电容器充电后两极板与电源断开,U、C、Q、E怎样随d、S变化
Q不变
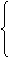 C↓
C↓
|
E===,保持不变
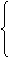 C↓
C↓
|
E===↑
16、电容
(1)电容器所带电荷量:电容器所带电荷量,是指每个极板所带电荷量的绝对值。
(2)电容
①定义:电容器所带电荷量Q与电容器两极板间的电势差U的比值,叫做电容器的电容。
②公式
用C表示电容,则有
C== (量度式)
上式表示,电容器的电容在数值上等于使两板间电势差为1 V时电容器所带电荷量。或等于使电容器两极板间电势差增加1V时所需的电荷量。需要的电荷量多,表示电容器的电容大。
③物理意义
电容是表示电容器容纳电荷本领的物理量,由电容器本身决定。
定义式C=为量度式,C不能说与Q成正比,与U成反比,C与Q、U无关。不论电容器是否带电,带多少电,两极板间的电势差是多少等,电容器的电容都是个定值。Q=CU,Q由C、U决定;U=,U由Q、C决定。
④单位
在国际单位制中,电容的单位是法拉,简称法,符号是F。如果一个电容器带1C的电量,两极板间的电势差是1V,这个电容器的电容就是1F。法拉这个单位太大,实际中常用较小的单位:微法(μF)和皮法(pF),它们与法拉的关系是:
1 F=106μF=1012pF
15、电容器
(1)电容器:任何两个彼此绝缘又相隔很近的导体,组成一个电容器。
(2)电容器的充放电
①充电:电容器两板分别接在电池两端,两板带上等量异种电荷的过程叫做充电。
在充电过程中,电路中有短暂的充电电流。
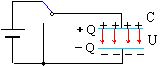 充电后,切断与电源的联系,两个极板上都保存有电荷,
充电后,切断与电源的联系,两个极板上都保存有电荷,
两极板间有电场存在。充电过程中由电源获得的电能储
存在电场中,称为电场能。
充电:电源能量→电场能。
②放电:充了电的电容器的两极板用导线相连,使两极板上正、
 负电荷中和的过程叫做放电。
负电荷中和的过程叫做放电。
在放电过程中,从灵敏电流计可以观察到有短暂的放电电流。
放电后,两极板间不存在电场,电场能转化为其它形式的能。
放电:电场能→其他形式能。
14、等势面的特点
(1)同一等势面上各点的电势相等,在同一等势面上移动电荷时电场力不做功。电荷从一个等势面上的任一点移到另一个等势面上的任一点,电势能的变化量相同,电场力做的功相同。
(2)等势面一定和电场线垂直,且电场线总是由电势较高的等势面指向电势较低的等势面。
(3)在相邻等势面间电势差值相同的情况下,等势面密处场强大,等势面疏处场强小。
(4)不同电势的等势面在空间不能相交,同一电势的等势面一般也不相交。
例题:下列说法中正确的是( )
A.某匀强电场若用相邻的两个等势面的电场差均相等的等势面来表示,则这些等势面一定是间隔相等的一系列平面
B.凡是场强不为零的匀强电场,一定能够用一些间隔相等、同一方向的平行电场线来描述
C.某非匀强电场,它的电场线图可能由间隔不等的同一方向的一些平行直线组成
D.如果在某电场中各点的电场线都是方向相同、相互平行的直线,那么这个电场一定是匀强电场 答:ABD
13、几种典型电场的等势面
(1)点电荷电场中的等势面,是以电荷为球心的一簇球面;
下图是点电荷电场中的等势面及与等高线对比的示意图。

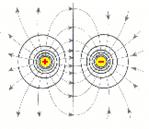
(2)等量异种点电荷电场中的等势面,是两簇对称曲面;
下图是等量异种点电荷电场中的等势面及与等高线对比的示意图。

(3)等量同种点电荷电场中的等势面,也是两簇对称曲面;
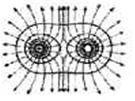 下图是等量同种点电荷电场中的等势面及与等高线对比的示意图。
下图是等量同种点电荷电场中的等势面及与等高线对比的示意图。

(4)匀强电场中的等势面,是垂直于电场线的一簇平面。
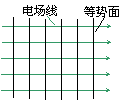
12、等势面
电场中电势相同的各点构成的面,叫等势面。
等势面不仅可形象描述电势,而且每相邻两等势面间距也可形象表示它们间的电势差。
11、电势能
(1)电势能
电荷在电场中具有的能,称之为电势能。
(2)电场力做功与电势能变化的关系
①电场力做正功时电势能减少
②电场力做负功时电势能增加
③电场力做功与电势能变化的关系
电势能的变化与电场力做的功的数值相等。电势能的增减可从物理意义上分析得出。
电场力做多少正功,电势能就减少多少。电场力做多少负功,电势能就增加多少。
W=εA-εB=-Δε
电势能的变化与电场力做的功的数值相等。电势能的增减可从物理意义上分析得出。
顺着电场线方向移动正电荷或逆着电场线方向移动负电荷时,电场力做正,电势能减少;逆着电场线移动正电荷或顺着电场线移动负电荷,电场力做负功,电势能增加。
(3)电势能的数值
电荷在电场中某点的电势能,在数值上等于把电荷从该点移动到电势能为零处电场力所做的功。
例1:在如图所示的电场中,已知A、B两点间的电势差UAB=-10V。
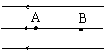 (1)电荷q=+4×10-9 C由A点移动到B点,电场力所做的功是多少?电势能是增加还是减少?
(1)电荷q=+4×10-9 C由A点移动到B点,电场力所做的功是多少?电势能是增加还是减少?
(2)电荷q=-2×10-9 C由A点移动到B点,电场力所做的功是多少?电势能是增加还是减少:
解析:从图中电场线的方向知道, A<
A< B,UAB=
B,UAB=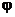 A-
A-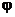 B<0,题中给出的UAB为负值。
B<0,题中给出的UAB为负值。
(1)电荷q=+4×10-9 C由A点移动到B点,电场力所做的功为
WAB=qUAB=4×10-9×(-10)J=-4×10-8J。
正电荷由A点移动到B点,电场力的方向与位移的方向相反,电场力做负功,即克服电场力做功。这时其它形式的能转化为电势能,电势能增加。
(2)电荷q=-2×10-9 C由A点移动到B点,电场力所做的功为
WAB=qUAB=-2×10-9×(-10)J=2×10-8J。
负电荷由A点移动到B点,电场力的方向与位移的方向相同,电场力做正功,这时电势能转化为其它形式的能,电势能减少。
总结:在应用公式WAB=qUAB进行计算时,式中的各个量可以取绝对值,功的正负则根据电场力的方向和位移的方向来判断。这时,公式可写成
W=qU。
不论电场如何分布,电场力是恒力还是变力,都可用W=qU来计算电功。
例2:将电荷量为6×10-6C的负电荷从电场中的A点移到B点,电荷克服电场力做了3×10-5J的功,再从B移到C,电场力做了1.2×10-5J的功,求
①A、C间的电势差UAC?
②电荷从A移到B,再从B移到C的过程中电势能共改变了多少?
解:①UAC===3V
②WAC=WAB+WBC=-3×10-5+1.2×10-5=-1.8×10-5J
可见电势能增加了1.8×10-5J。
⑷关于能量的转化和守恒定律在电场中的应用
①如果只有电场力对带电粒子做功
电场力对带电粒子所做的正功,等于其电势能减少量,也等于其动能的增加量;带电粒子反抗电场力所做的功(电场力对带电粒子做负功),等于其电势能的增加量,也等于其动能的减少量.
总之,带电粒子在电场里运动的过程中,如果只有电场力对带电粒子做功,那么带电粒子的动能和电势能互相转化,而且动能和电势能的总和保持不变.
②如果电场和重力都对带电微粒做功,此外其他力不做功.那么,带电微粒的电势能和机械能互相转化,而且带电微粒的电势能和机械能的总和保持不变.
10、电势
(1)电势
电场中某点的电势,等于单位正电荷由该点移到参考点(零电势点)时电场力所做的功。
UAB=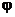 A-
A-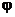 B
B
UBA=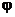 B-
B-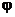 A
A
例题: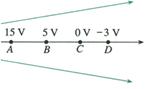 在图中所示的电场中,取C点为零电势点,1C的正电荷分别由A、B、D三点移动到C点时,电场力所做的功分别是15J、5J、-3J,这三点的电势就分别是
在图中所示的电场中,取C点为零电势点,1C的正电荷分别由A、B、D三点移动到C点时,电场力所做的功分别是15J、5J、-3J,这三点的电势就分别是 A=15V,
A=15V,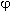 B=5V,
B=5V,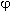 D=-3V。
D=-3V。
有了电势的概念,即可用两点的电势的差值来表示两点间的电势差。
UAB=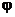 A-
A-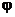 B
B
UBA= B-
B- A
A
 A、B两点间的电势差UAB =
A、B两点间的电势差UAB =  A-
A-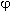 B = 15V-5V=10V,D、A两点间的电势差UDA =
B = 15V-5V=10V,D、A两点间的电势差UDA = 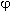 D-
D-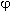 A =-3V-15V=-18V。
A =-3V-15V=-18V。
(2)电势的数值是相对的
电场中某点的电势与零电势点的选取有关,
电场中某点的电势的数值是相对的。
(3)电势是标量
电势是标量,电势的正、负表示该点的电势比零电势高还是低。
(4)物理意义
电势是描述电场中一点的能的性质的物理量。
(5)沿电场线的方向,电势越来越低
电场中电势的高低可以根据电场线的方向来判断。
如何判断电势高低呢?
分析:只要两点间的电势差的情况了解了,电势高低即可清楚,故可取一电荷在电场中移动讨论电场力做功。
在电场中移动电荷时,有下面的四种典型情况:

沿着电场线移动正电荷,电场力做正功;逆着电场线移动正电荷,电场力做负功;沿着电场线移动负电荷,电场力做负功;逆着电场线移动负电荷,电场力做正功。
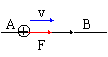 沿着电场线的方向将单位正电荷由A点移动B点,电场力做正功:
沿着电场线的方向将单位正电荷由A点移动B点,电场力做正功:
UAB=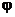 A-
A-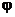 B>0
B>0
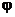 A>
A>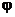 B
B
结论:沿电场线方向,电势逐渐降低。
沿电场线的方向,电势越来越低。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com