12、轨道半径和周期

(1)轨道半径公式：由qvB＝m可得

r＝

上式告诉我们，在匀强磁场中做匀速园周运动的带电粒子，它的轨道半径跟粒子的运动速率成正比。运动的速度越大，轨道的半径也越大。

(2)周期公式

将半径r代入周期公式T＝中，得到

T＝

带电粒子在磁场中做匀速圆周运动的周期跟轨道半径和运动速率无关。

(3)频率公式：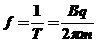

(4)角频率(角速度)公式：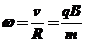

例题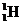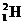：、、它们以下列情况垂直进入同一匀强磁场，求轨道半径之比。

①具有相同速度；

②具有相同动量；

③具有相同动能。

解答：依据qvB＝m，得r＝

①v、B相同，所以r∝，所以r₁∶r₂∶r₃＝1∶2∶2

②因为mv、B相同，所以r∝，r₁∶r₂∶r₃＝2∶2∶1

③mv²相同，v∝，B相同，所以r∝，所以r₁∶r₂∶r₃＝1∶∶1。

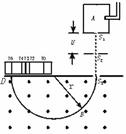例题：如图所示，一质量为m，电荷量为q的粒子从容器A下方小孔S₁飘入电势差为U的加速电场。然后让粒子垂直进入磁感应强度为B的磁场中做匀速园周运动，最后打到照相底片D上，如图所示。求

①粒子进入磁场时的速率；

②粒子在磁场中运动的轨道半径。

解答：①粒子在S₁区做初速度为零的匀加速直线运动。在S₂区做匀速直线运动，在S₃区做匀速圆周运动。

由动能定理可知

mv²＝qU

由此可解出

v＝

②粒子在磁场中做匀速圆周运动的轨道半径为

r＝＝

11、带电粒子在匀强磁场中的运动

(1)带电粒子的运动方向与磁场方向平行

当带电粒子的运动方向与磁场方向平行时，粒子不受洛伦兹力。所以，此时粒子做匀速直线运动。

(2)带电粒子的运动方向与磁场方向垂直

①运动轨迹

垂直射入匀强磁场中的带电粒子，在洛伦兹力F＝qvB的作用下，将会偏离的运动方向。粒子在匀强磁场中做匀速圆周运动。

②带电粒子的受力及运动分析

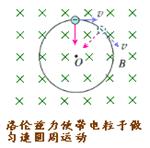
洛伦兹力只改变速度的方向，不改变速度的大小，提供电子做匀速园周运动的向心力。

　(3)带电粒子的运动方向与磁场方向成θ角

粒子在垂直于磁场方向作匀速圆周运动，在磁场方向作匀速直线运动。叠加后粒子作等距螺旋线运动。

5、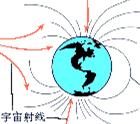宇宙射线：运动电荷在磁场中受到洛伦兹力的作用，运动方向会发生偏转，这一点对于地球上的生命来说有十分重要的意义.从太阳或其他星体上，时刻都有大量的高能粒子流放出，称为宇宙射线，这些高能粒子流，如果都到达地球，将对地球上的生物带来危害.庆幸的是，地球周围存在地磁场，地磁场改变宇宙射线中带电粒子的运动方向，对宇宙射线起了一定的阻挡作用。

宇宙射线是穿透力极强的辐射线，它们来自宇宙空间，从各个方向射向地球，20世纪初，我们想要获得一个不受辐射影响的实验环境，总是不能如愿，即使深入矿井内部，仍然摆脱不开宇宙射线穿透性辐射的干扰，1912年，奥地利物理学家海斯乘气球升空去探寻这些辐射的来源，他发现，在气球上升过程中，辐射不是减弱而是增强了，后来又发现，两极地区的辐射更为强大，说明它似乎受地球磁场的影响，表明它含有带电粒子(如质子)，宇宙射线中的带电粒子在穿越地磁场过程中，受到地磁场对它们的洛伦兹力的作用，运动方向会发生偏转，对宇宙射线有一定的阻挡作用，大大减弱了到达地球表面的宇宙射线。

例题：如图所示，一个带正电q的小带电体处于垂直纸面向里的匀强磁场中，磁感应强度为B，若小带电体的质量为m，为了使它对水平绝缘面正好无压力，应该(　 )

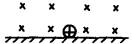A．使B的数值增大

B．使磁场以速率 v＝，向上移动

C．使磁场以速率v＝，向右移动

D．使磁场以速率v＝，向左移动

解析：为使小球对平面无压力，则应使它受到的洛伦兹力刚好平衡重力，磁场不动而只增大B，静止电荷在磁场里不受洛伦兹力， A不可能；磁场向上移动相当于电荷向下运动，受洛伦兹力向右，也不可能平衡重力，故B、C也不对；磁场以V向左移动，等同于电荷以速率v向右运动，此时洛伦兹力向上。当 qvB＝mg时，带电体对绝缘水平面无压力，则v＝，选项 D正确。

关于带电小球在匀强磁场中的运动

例题： 单摆摆长L，摆球质量为m，带有电荷+q，在垂直于纸面向里的磁感应强度为B的匀强磁场中摆动，当其向左、向右通过最低点时，线上拉力大小是否相等？

解析：摆球所带电荷等效于一个点电荷，它在磁场中摆动时受到重力mg，线的拉力F与洛伦兹力 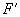，由于只有重力做功，及机械能守恒，所以摆球向左、向右通过最低点时的速度大小是相同的，设为V，向在通过最低点时洛仑兹力 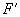竖直向下，根据牛顿第二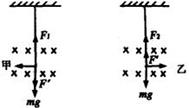定律，如图有

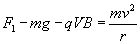
故有

当向右通过最低点时，洛伦兹力 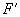的竖直向上，而大小仍为qvB，同理可得

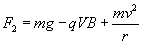
显然F₁＞F₂

4、洛伦兹力的特点

(1)运动的电荷才在可能受到洛伦兹力，静止的电荷在磁场中不受洛伦兹力。

(2)洛仑兹力的大小和方向都与带电粒子运动状态有关。

(3)洛仑兹力对运动电荷不做功，不会改变电荷运动的速率。

洛伦兹力的方向垂直于v和B组成的平面，即洛伦兹力垂直于速度方向，因此，洛伦兹力只改变速度的方向，不改变速度的大小，所以洛伦兹力对电荷不做功。

3、洛伦兹力的大小

(1)洛伦兹力的推导

若有一段长度为L的通电导线，横截面积为S，单位体积中含有的自由电荷数为n，每个自由电荷的电荷量为q，定向移动的平均速率为v，将这段导线垂直于磁场方向放入磁感应强度为B的匀强磁场中。

这段导体所受的安培力为F_安＝BIL

电流强度I的微观表达式是I＝nqSv

这段导体中含有的电荷数为nLS

每个自由电荷所受的洛伦兹力大小为F＝＝＝＝qvB

(2)洛伦兹力公式：F＝qvB

公式中各量的单位：F为N，q为C，v为m/s，B为T。

(3)适用条件

电荷的运动方向与磁场方向垂直，即v⊥B。

若v与B方向成某一角度θ时，洛沦兹力的分式为：F＝qvBsinθ。

说明：①θ角为电荷运动方向和磁场方向的夹角；

②θ＝90°时F＝qvB；θ＝0°时F＝0。

③因为B为矢量，Bsinθ为B在垂直于v方向上的分量；Bcosθ为B沿v方向上的分量。

④因为v为矢量：F＝qvBsinθ可写成F＝qBvsinθ。vsinθ理解为v在垂直于B方向上的分量。

例题：电子的速率v＝3×10⁶ m/s，垂直射入B＝0.10 T的匀强磁场中，它受到的洛伦兹力是多大？

F＝qvB＝1.60×10^－19×3×10⁶×0.10N＝4.8×10^－14 N。

例题：来自宇宙的质子流，以与地球表面垂直的方向射向赤道上空的某一点，则这些质子在进入地球周围的空间时，将(　　)

A．竖直向下沿直线射向地面　　　　　 B．相对于预定地面向东偏转

C．相对于预定点稍向西偏转　　　　　 D．相对于预定点稍向北偏转

分析：B项正确。地球表面地磁场方向由南向北，质子是氢原子核带正电，根据左手定则可判定，质子自赤道上空竖直下落过程中受洛伦兹力方向向东。

例题：电视机显像管的偏转线圈示意图如右，即时电流方向如图所示。该时刻由里向外射出的电子流将向哪个方向偏转？

解：画出偏转线圈内侧的电流，是左半线圈靠电子流的一侧为向里，右半线圈靠电子流的一侧为向外。电子流的等效电流方向是向里的，根据“同向电流互相吸引，反向电流互相排斥”，可判定电子流向左偏转。(本题用其它方法判断也行，但不如这个方法简洁)。

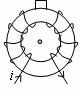
2、洛伦兹力的方向

洛伦兹力方向的判断──左手定则

伸开左手，使大拇指和其余四指垂直，且处于同一平面内，把手放入磁场中，让磁感线垂直穿入手心，四指指向正电荷运动的方向，那么，拇指所指的方向就是正电荷所受洛伦兹力的方向。

运动的负电荷在磁场中所受的洛伦兹力，方向跟正电荷受的力相反。在用左手定则判断时，若四指指向是电荷运动的反方向，那么拇指所指的方向就是负电荷所受洛伦兹力的方向。

1、概念：运动电荷在磁场中受到的作用力，叫做洛伦兹力。

荷兰物理学家洛伦兹首先提出了运动电荷产生磁场和磁场对运动电荷有作用力的观点，为纪念他，人们称这种力为洛伦兹力。通电导线在磁场中所受安培力是洛伦兹力的宏观表现。

10、洛伦兹力：

9、电流表的工作原理

(1)电流表的工作原理

线框所受安培力的力矩应为

M₁＝NBIS

弹簧产生的弹性力矩M₂与指针的偏转角度θ成正比，即M₂＝kθ。

当M₁＝M₂时，线圈就停在某一偏角θ上。

由M₁＝M₂可得

NBIS＝kθ

θ＝·I

从公式中可以看出：

①对于同一电流表N、B、S和k为不变量，所以θ∝I，可见θ与I一一对应，从而用指针的偏角来测量电流I的值；

②因θ∝I，θ随I的变化是线性的，所以表盘的刻度是均匀的。

　(2)磁电式仪表的优缺点

利用充当永久磁铁使通电线圈偏转的仪器叫做磁电式仪表

磁场对电流的作用力和电流成正比，因而线圈中的电流越大，安培力产生的力矩也越大，线圈和指针偏转的角度也越大，因此，根据指针偏转角度的大小，可以知道被测电流的强弱.当线圈中的电流方向改变时，安培力的方向随着改变，指针的偏转方向也随着改变，所以，根据指针的偏转方向，可以知道被测电流的方向。

磁电式仪表的优点是刻度均匀、准确度高、灵敏度高，可以测出很弱的电流；缺点是价格较贵，绕制线圈的导线很细，允许通过的电流很弱(几十微安到几毫安).如果通过的电流超过允许值，很容易把它烧坏。

8、线框在匀强磁场中的磁力矩

(1)线圈平面与磁场方向平行

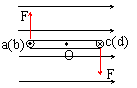
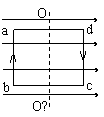例题：如图所示，单匝矩形线圈的边长分别为ab＝cd＝L₁，bc＝ad＝L₂，它可以绕对称轴OO′转动，线圈中的电流强度为I，线圈处于磁感应强度B的匀强磁场中，当线圈平面与磁场平行时，求线圈所受的安培力的总力矩。

解析：线圈平面与磁场平行时，线圈中只有ab、cd两边受力。所受力如图所示，两边安培力的大小为

F＝BIL₁

这一对力偶的力偶臂为L₂，所受安培力的总力矩

M＝BIL₁L₂＝BIS

拓展：如果是n匝线圈，则线圈所受安培力的力矩为多大？

如果是n匝线圈，则线圈所受安培力的力矩为M＝nBIS

当线圈平面与磁感线平行时，线圈受到的安培力的力矩为最大。

(2)线圈平面与磁场方向成α角：M＝nBIScosα＝M_mcosα

(3)线圈平面与磁场方向垂直：M＝0。

(4)说明①上式只适用于匀强磁场；

②在匀强磁场中，当转轴OO′⊥B的时，M与转轴的位置及线圈的形状无关。

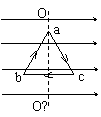例题：如图所示，一正三角形线圈，放在匀强磁场中，磁场与线圈平面平行，设I＝5 A，磁感应强度B＝1.0 T，三角形边长L＝30cm.。求线圈所受磁力矩的大小及转动方向(电流方向为acba)。

解法一：因为在匀强磁场中，在转轴OO′和B相垂直的条件下，M与转轴的位置和线圈的形状无关。所以

M＝BIS＝0.2 N·m。

根据左手定则ab边受的安培力方向垂直于ab边向下，ac边受的安培力方向垂直于ac边向上，所以线圈的转动方向为：从上往下看为顺时针转动。

解法二：bc边不受安培力；ab、ac受力等大反向，可认为安培力作用在它们的中点，磁力矩为

M＝2F×sin30°

F＝BILcos30°

由以上二式求出

M＝0.2 N·m

从上往下看转动方向为顺时针方向。