1．物块静止在固定的斜面上，分别对物块施加大小相等的力F，施力后物块仍然静止。则力F使物块所受的静摩擦力增大的是.　　　　　　　　　　　　　 (　 　　)

A．F的方向垂直于斜面向上

B．F的方向垂直于斜面向下

C．F的方向竖直向上

D．F的方向竖直向下

6、北京商业中心分布和变化分为----------、--------------------、-----------------------的出现三个阶段。

5、沈大高速线旁有大型服装市场因为有 ------交通，可以吸引大量的-------，获得较高的---------。商业这种分布体现-----------原则。

4、山区比平原区商业网点-----，因为山区交通-------，交通线路------，交通运输方式-------，

3、扬州兴盛原因是-----------的开凿，后来的衰落是因为----------淤塞，加之--------发展以及--------线修筑，使大运河的------衰落，城市也随之衰落，

2、嘉兴最初是-------地域形态，后来演变成------，-------，最后演变为------状。是由于----------发展变化造成的。

1、株洲和筑波两个城市呈--------分布。都是沿---------发展的。

15．已知函数y＝f(x)是定义在R上的周期函数，周期T＝5，函数y＝f(x)(－1≤x≤1)是奇函数．又知y＝f(x)在[0,1]上是一次函数，在[1,4]上是二次函数，且在x＝2时函数取得最小值，最小值为－5.

(1)证明：f(1)+f(4)＝0；

(2)试求y＝f(x)，x∈[1,4]的解析式；

(3)试求y＝f(x)在[4,9]上的解析式．

(1)证明：∵y＝f(x)是以5为周期的周期函数，

∴f(4)＝f(4－5)＝f(－1)．

又y＝f(x)(－1≤x≤1)是奇函数，

∴f(1)＝－f(－1)＝－f(4)．

∴f(1)+f(4)＝0.

(2)解：当x∈[1,4]时，由题意，可设

f(x)＝a(x－2)²－5　(a≠0)

由f(1)+f(4)＝0得

a(1－2)²－5+a(4－2)²－5＝0

解得a＝2.

∴f(x)＝2(x－2)²－5　(1≤x≤4)．

(3)解：∵y＝f(x)　(－1≤x≤1)是奇函数，

∴f(0)＝－f(－0)．∴f(0)＝0.

又y＝f(x)　(0≤x≤1)是一次函数，

∴可设f(x)＝kx(0≤x≤1)，

∵f(1)＝2(1－2)²－5＝－3，

又f(1)＝k·1＝k，

∴k＝－3.

∴当0≤x≤1时，f(x)＝－3x；

当－1≤x<0时，0<－x≤1.

∴f(x)＝－f(－x)＝－3x.

∴当－1≤x≤1时，f(x)＝－3x；

当4≤x≤6时，－1≤x－5≤1，

∴f(x)＝f(x－5)＝－3(x－5)＝－3x+15；

当6<x≤9时，1<x－5≤4，

f(x)＝f(x－5)＝2[(x－5)－2]²－5＝2(x－7)²－5.

∴f(x)＝

14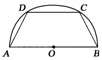．如右图所示，有一块半径为R的半圆形钢板，计划剪裁成等腰梯形ABCD的形状，它的下底AB是⊙O的直径，且上底CD的端点在圆周上，写出梯形周长y关于腰长x的函数关系式，并求出它的定义域．

解：AB=2R.

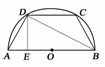C、D在⊙O的半圆周上，

设腰长AD=BC=x，作DE⊥AB，

垂足为E，连接BD，

那么∠ADB是直角，

由此Rt△ADE∽Rt△ABD.

∴AD²=AE×AB，即AE=，

∴CD=AB-2AE=2R-，

所以y=2R+2x+(2R-)，即y=-+2x+4R.

再由，解得0<x<R.

所以y＝－+2x+4R，定义域为(0，R)．

13．已知函数f(x)和g(x)的图象关于原点对称，且f(x)＝x²+2x.

(1)求g(x)的解析式；

(2)解不等式g(x)≥f(x)－|x－1|.

解：(1)设函数y＝f(x)的图象上任一点Q(x₀，y₀)关于原点的对称点为P(x，y)，

则　即

∵点Q(x₀，y₀)在函数y＝f(x)的图象上，

∴－y＝x²－2x，即y＝－x²+2x，

故g(x)＝－x²+2x.

(2)由g(x)≥f(x)－|x－1|可得：2x²－|x－1|≤0.

当x≥1时，2x²－x+1≤0，此时不等式无解．

当x<1时，2x²+x－1≤0，∴－1≤x≤.

因此，原不等式的解集为[－1，]．