
5.2; 6. 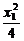 +
+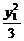 =1,
=1, 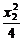 +
+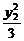 =1.相减得
=1.相减得
∴ =-
=-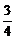 ·
· .
.
又∵M为AB中点,x1+x2=2,y1+y2=2.
∴直线l的斜率为-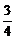 .
.
得直线l的方程为3x+4y-7=0.
4.设左焦点为F1,右焦点为F2,由双曲线定义和三角形边的关系得:
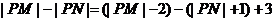
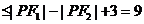 ,选D
,选D
6. 直线l过点M(1,1),与椭圆 +
+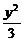 =1相交于A、B两点,若AB的中点为M,则直线l的方程是________.
=1相交于A、B两点,若AB的中点为M,则直线l的方程是________.
简答:1-4.BCBD;
5.(2005山东)设直线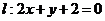 关于原点对称的直线为
关于原点对称的直线为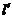 ,若
,若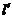 与椭圆
与椭圆 的交点为A、B,点
的交点为A、B,点 为椭圆上的动点,则使
为椭圆上的动点,则使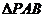 的面积为
的面积为 的点
的点 的个数为______.
的个数为______.
4.(2006江西) 为双曲线
为双曲线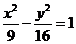 的右支上一点,
的右支上一点,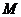 、
、 分别是圆
分别是圆
 上的点,则
上的点,则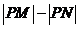 的最大值为( )
的最大值为( )
A.6 B.7 C.8 D.9
3.(2006江苏)已知两点M(-2,0)、N(2,0),点P为坐标平面内的动点,满足 =0,则动点P(x,y)的轨迹方程为( )
=0,则动点P(x,y)的轨迹方程为( )
(A)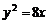 (B)
(B)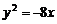 (C)
(C)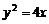 (D)
(D)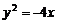
2.已知双曲线的两个焦点是椭圆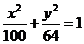 的两个顶点,双曲线的两条准线经过椭圆的两个焦点,则此双曲线的方程是 ( )
的两个顶点,双曲线的两条准线经过椭圆的两个焦点,则此双曲线的方程是 ( )
A.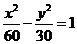 B.
B.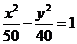 C.
C.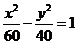 D.
D.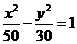
1.(2005北京)设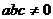 ,“
,“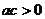 ”是“曲线
”是“曲线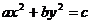 为椭圆”的( )
为椭圆”的( )
A.充分非必要条件 B.必要非充分条件
C.充分必要条件 D.既非充分又非必要条件
解析几何是以数来研究形的学科,就是数形结合的学科;解析法就是通过坐标、方程所反映的数量间的关系和特征,来研究图形的几何性质。
圆锥曲线的综合问题包括:解析法的应用,数形结合的思想,与圆锥曲线有关的定值、最值等问题;有圆锥曲线科内综合,还有与代数、三角、几何、向量等学科间的综合。
复习中应注意掌握解析几何的常用方法,如求曲线方程的方法、研究位置关系的方法、求范围与最值的方法等,通过问题的解决,进一步培养函数与方程、等价转化、分类讨论等数学思想。
4.了解圆锥曲线的初步应用,掌握处理圆锥曲线综合问题的常用方法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com