
3.曲线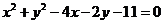 上到直线
上到直线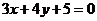 距离等于1的点的个数为
距离等于1的点的个数为
A.1 B.2 C.3 D.4
2.复数 的共轭复数
的共轭复数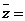
A.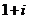 B.
B.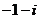 C.
C.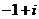 D.
D.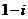
有一项是符合题目要求的,)
1.不等式 的解集为
的解集为
A. B.
B.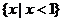
C.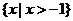 D.
D.
22.(本小题满分14分)
已知函数f(x)=ln(x+a)-x2-x在x = 0处取得极值.
(I)求实数a的值;
(Ⅱ)若关于x的方程,f(x)=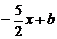 在区间[O,2]上恰有两个不同的实数根,求实数b的取值范围;
在区间[O,2]上恰有两个不同的实数根,求实数b的取值范围;
(Ⅲ)证明:对任意的正整数n,不等式ln  都成立.
都成立.
2009年福建省普通高中毕业班质量检查
21.(本小题满分12分)
 已知定点A(a,O)( a >0),B为x轴负半轴上的动点.以AB为边作菱形ABCD,使其两对角线的交点恰好落在y轴上.
已知定点A(a,O)( a >0),B为x轴负半轴上的动点.以AB为边作菱形ABCD,使其两对角线的交点恰好落在y轴上.
(I)求动点D的轨迹E的方程;
(Ⅱ)过点A作直线l与轨迹E交于P、Q两点,设点R (- a,0),问当l绕点A转动时,∠PRQ是否可以为钝角?请给出结论,并加以证明.
20.(本小题满分12分)
国际上钻石的重量计量单位为克拉.已知某种钻石的价值υ(美元)与其重量ω (克拉)的平方成正比,且一颗重为3克拉的该种钻石的价值为54000美元.
(I)写出υ关于ω的函数关系式;
(Ⅱ)若把一颗钻石切割成重量比为1∶3的两颗钻石,求价值损失的百分率;
(Ⅲ)试用你所学的数学知识证明:把一颗钻石切割成两颗钻石时,按重量比为1:1切割,价值损失的百分率最大.
(注:价值损失的百分率= ×100%;在切割过程中的重量损耗忽略不计)
×100%;在切割过程中的重量损耗忽略不计)
19.(本小题满分12分)
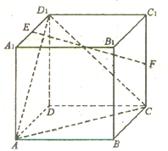 如图,在棱长为2的正方体ABCD -A1B1C1D1中,E、F分别为AA1,和CC1的中点.
如图,在棱长为2的正方体ABCD -A1B1C1D1中,E、F分别为AA1,和CC1的中点.
(I)求证:EF∥平面ACD,;
(Ⅱ)求异面直线EF与AB所成的角;
(Ⅲ)在棱BB1上是否存在一点P,使得二面角P-AC-B的大小为30°?若存在,求出BP的长;若不存在,请说明理由.
18.(本小题满分12分)
在数列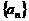 中,a1=1,an+1=
中,a1=1,an+1=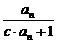 (c为常数,n∈N*),且a1,a2,a5成公比不等于1的等比数列.
(c为常数,n∈N*),且a1,a2,a5成公比不等于1的等比数列.
(I)求证:数列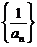 是等差数列;
是等差数列;
(Ⅱ)求c的值;
(Ⅲ)设bn=anan+1,数列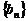 的前n项和为Sn,求
的前n项和为Sn,求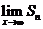 .
.
17.(本小题满分12分)
已知函数f(x)=cos2x+sinxcosx(x∈R)
(I)求f( )的值;
)的值;
(Ⅱ)求f(x)的单调递增区间.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com