2．下列函数中既是奇函数，又在区间(0，+∞)上单调递增的是

　　　 A．y＝sinx　　　　　　　　　 B．y＝－x²　　　　　 C．y＝lg2^x 　　　　　　　　 D．y＝e|x|

1．已知集合M＝|0，a|，N＝|x|x²－2x－3<0,x∈Z|，若M∩N≠，则a的值为

　　　 A．1　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．2

C．1或2　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．不为零的任意实数

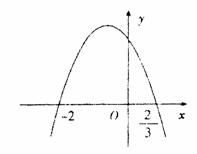
22．(本小题满分12分)设的极小值为－8，其导函数的图象经过点，如图所示。

　 (1)求的解析式；

　 　 (2)若对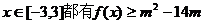恒成立，求实数m的取值范围。

21．(本小题满分12分)已知，椭圆的焦点为顶点，以双曲线的顶点为焦点。

　 (1)求椭圆C的方程；

　 (2)若直线与椭圆C相交于M、N两点(M、N不是左右顶点)，且以线段MN为直径的圆过点A，求证：直线l过定点，并求出该定点的坐标。

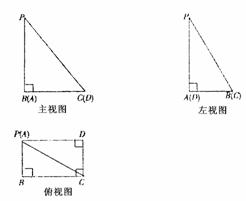
20．(本小题满分12分)如图是一个几何体的三视图，请认真读图。

　 (1)有人说该几何体的侧棱PA垂直于底面ABCD，有人说四边形ABCD为矩形，也有人说PA不垂直于底面，请根据你的判断画出几何体的直观图；

　 (2)设AB的中点为M，PC中点为N，求证：MN//平面PAD；

　 　 (3)当AB=BC时，求证：平面PAC⊥平面BND。

19．(本题满分2分)为了支持其贫困山区学校的教学工作，某市决定从5位优秀教师(二位女教师，三位男教师)中选派3位教师去该山区学校担任支教教师。设选派的3名老师中恰有2位女教师的概率为P(A)；选派3名教师中至少有一位女教师的概率为P(B)。

　 (1)求P(A)；

　 (2)求P(B)；

　 (3)设函数，记“在函数定义域内任取一点x₀，则”为事件C，求事件C的概率。

18．(本小题满分12分)数列

　 (1)求证：数列是等比数列；

　 (2)求数列{}的通项公式；

　 (3)

17．(本小题满分12分)若向量

的图象中，对称中心到对称轴的最小距离为 时，的最大值为1。

　 (1)求函数的解析式；

　 (2)求函数的单调递增区间。

16．设函数上的奇函数，且满足都成立，又当时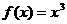，，则下列四个命题：

　　　 ①函数以4为周期的周期函数；　 ②当[1，3]时，；

　　　 ③函数的图象关于x=1对称；　 ④函数的图象关于点(2，0)对称，

其中正确的命题序号是　　　　　 。

15．已知a、b都是正实数，且满足的最小值为　　　　　 。