
4. 选修4-5:不等式选讲
已知x,y,z均为正数.求证: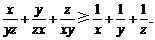
证明:因为x,y,z无为正数.所以 , ………………………………4分
, ………………………………4分
同理可得 ,………………………………………………………7分
,………………………………………………………7分
当且仅当x=y=z时,以上三式等号都成立.
将上述三个不等式两边分别相加,并除以2,得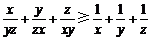 .…………10分
.…………10分
3. 选修4-4:坐标系与参数方程
过点P(-3,0)且倾斜角为30°的直线和曲线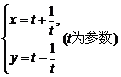 相交于A、B两点.求线段AB的长.
相交于A、B两点.求线段AB的长.
解:直线的参数方程为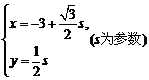 ,………………………………………………3分
,………………………………………………3分
曲线 可以化为
可以化为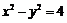 .……………………………………………5分
.……………………………………………5分
将直线的参数方程代入上式,得 .
.
设A、B对应的参数分别为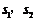 ,∴
,∴ .…………………………8分
.…………………………8分
AB =
=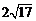 .…………………………………………………10分
.…………………………………………………10分
说明:掌握直线,圆,圆锥曲线的参数方程及简单的应用.
2. 选修4-2:矩阵与变换
 如图所示, 四边形ABCD和四边形
如图所示, 四边形ABCD和四边形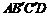 分别是矩形和平行四边
分别是矩形和平行四边
形,其中点的坐标分别为A(-1,2),B(3,2),C(3,-2),
D(-1,-2), (3,7),
(3,7),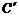 (3,3).求将四边形ABCD变成
(3,3).求将四边形ABCD变成
四边形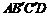 的变换矩阵M.
的变换矩阵M.
解:该变换为切变变换,设矩阵M为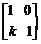 ,…………………3分
,…………………3分
则 .………………………………………………6分
.………………………………………………6分
∴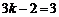 ,解得
,解得 .…………………………………………………………………9分
.…………………………………………………………………9分
所以,M为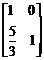 .………………………………………………………………………10分
.………………………………………………………………………10分
说明:掌握几种常见的平面变换.
1. 选修4-1:几何证明选讲
 如图,四边形ABCD内接于
如图,四边形ABCD内接于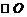 ,
, ,过A点的切线交CB
,过A点的切线交CB
的延长线于E点.
求证: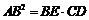 .
.
证明:连结AC.…………………………………………………1分
因为EA切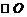 于A, 所以∠EAB=∠ACB.…………3分
于A, 所以∠EAB=∠ACB.…………3分
 因为
因为 ,所以∠ACD=∠ACB,AB=AD.
,所以∠ACD=∠ACB,AB=AD.
于是∠EAB=∠ACD.…………………………………5分
又四边形ABCD内接于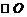 ,所以∠ABE=∠D.
,所以∠ABE=∠D.
所以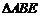 ∽
∽ .
.
于是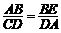 ,即
,即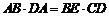 .………………9分
.………………9分
所以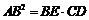 .…………………………………10分
.…………………………………10分
20.(本小题满分16分)
已知数列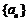 中,
中, ,且对
,且对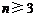 时,有
时,有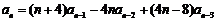 .
.
(Ⅰ)设数列 满足
满足 ,证明数列
,证明数列 为等比数列,并求数列
为等比数列,并求数列 的通项公式;
的通项公式;
(Ⅱ)记 ,求数列
,求数列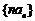 的前n项和Sn.
的前n项和Sn.
(Ⅰ) 证明:由条件,得 ,
,
则 .……………………………………2分
.……………………………………2分
即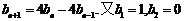 ,所以
,所以 ,
,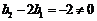 .
.
所以 是首项为
是首项为 2,公比为2的等比数列. …………………………………4分
2,公比为2的等比数列. …………………………………4分
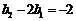 ,所以
,所以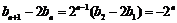 .
.
两边同除以 ,可得
,可得 .…………………………………………………6分
.…………………………………………………6分
于是 为以
为以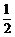 首项,-
首项,-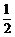 为公差的等差数列.
为公差的等差数列.
所以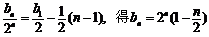 .………………………………………………8分
.………………………………………………8分
(Ⅱ) ,令
,令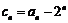 ,则
,则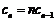 .
.
而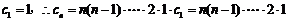 .
.
∴ . ……………………………………………………………12分
. ……………………………………………………………12分
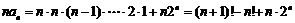 ,
,
∴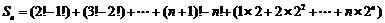 .………………14分
.………………14分
令Tn=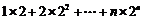 , ①
, ①
则2Tn= . ②
. ②
①-②,得 Tn=
Tn= ,Tn=
,Tn= .
.
∴ .……………………………………………………………16分
.……………………………………………………………16分
评讲建议:
此题主要考查数列的概念、等差数列、等比数列、数列的递推公式、数列的通项求法、数列前n项和的求法,作新数列法,错项相消法,裂项法等知识与方法,同时考查学生的分析问题与解决问题的能力,逻辑推理能力及运算能力.讲评时着重在正确审题,怎样将复杂的问题化成简单的问题,本题主要将一个综合的问题分解成几个常见的简单问题.事实上本题包含了好几个常见的数列题.本题还有一些另外的解法,如第一问的证明还可以直接代.
B.附加题部分
19.(本小题满分16分)
已知函数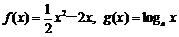 (a>0,且a≠1),其中为常数.如果
(a>0,且a≠1),其中为常数.如果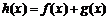 是增函数,且
是增函数,且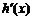 存在零点(
存在零点(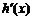 为
为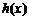 的导函数).
的导函数).
(Ⅰ)求a的值;
(Ⅱ)设A(x1,y1)、B(x2,y2)(x1<x2)是函数y=g(x)的图象上两点,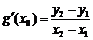 (
(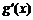 为
为 的导函数),证明:
的导函数),证明: .
.
解:(Ⅰ)因为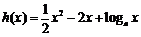
 ,
,
所以 . …………………………………………3分
. …………………………………………3分
因为h(x)在区间 上是增函数,
上是增函数,
所以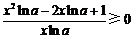 在区间
在区间 上恒成立.
上恒成立.
若0<a<1,则lna<0,于是 恒成立.
恒成立.
又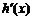 存在正零点,故△=(-2lna)2-4lna=0,lna=0,或lna=1与lna<0矛盾.
存在正零点,故△=(-2lna)2-4lna=0,lna=0,或lna=1与lna<0矛盾.
所以a>1.
由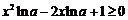 恒成立,又
恒成立,又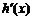 存在正零点,故△=(-2lna)2-4lna=0,
存在正零点,故△=(-2lna)2-4lna=0,
所以lna=1,即a=e. ……………………………………………………………………7分
(Ⅱ)由(Ⅰ), ,于是
,于是 ,
,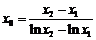 .…………………………9分
.…………………………9分
以下证明 . (※)
. (※)
(※)等价于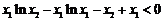 . ……………………………………………11分
. ……………………………………………11分
令r(x)=xlnx2-xlnx-x2+x,…………………………………………………………13分
r ′(x)=lnx2-lnx,在(0,x2]上,r′(x)>0,所以r(x)在(0,x2]上为增函数.
当x1<x2时,r(x1)< r(x2)=0,即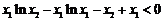 ,
,
从而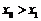 得到证明.……………………………………………………………………15分
得到证明.……………………………………………………………………15分
对于 同理可证……………………………………………………………16分
同理可证……………………………………………………………16分
所以 .
.
评讲建议:
此题主要考查函数、导数、对数函数、二次函数等知识.评讲时注意着重导数在研究函数中的应用.本题的第一小题是常规题比较容易,第二小题是以数学分析中的中值定理为背景,作辅助函数,利用导数来研究函数的性质,是近几年高考的热点.第二小题还可以这样证明:
要证明 ,只要证明
,只要证明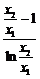 >1,令
>1,令 ,作函数h(x)=t-1-lnt,下略.
,作函数h(x)=t-1-lnt,下略.
18.(本小题满分15分)
已知椭圆 的左焦点为F,左、右顶点分别为A、C,上顶点为B.过F、B、
的左焦点为F,左、右顶点分别为A、C,上顶点为B.过F、B、
C作⊙P,其中圆心P的坐标为(m,n).
(Ⅰ)当m+n>0时,求椭圆离心率的范围;
(Ⅱ)直线AB与⊙P能否相切?证明你的结论.
解:(Ⅰ)设F、B、C的坐标分别为(-c,0),(0,b),(1,0),则FC、BC的中垂线分别为
 ,
, .………………………………………………………………2分
.………………………………………………………………2分
联立方程组,解出 ……………………………………………………………4分
……………………………………………………………4分
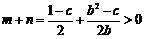 ,即
,即 ,即(1+b)(b-c)>0,
,即(1+b)(b-c)>0,
∴ b>c. ……………………………………………………………………………………6分
从而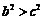 即有
即有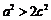 ,∴
,∴ .……………………………………………………7分
.……………………………………………………7分
又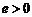 ,∴
,∴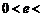
 . …………………………………………………………………8分
. …………………………………………………………………8分
(Ⅱ)直线AB与⊙P不能相切.…………………………………………………………………9分
由 ,
,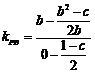 =
=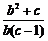 . ………………………………………………10分
. ………………………………………………10分
如果直线AB与⊙P相切,则 ·
·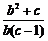 =-1. ………………………………………12分
=-1. ………………………………………12分
解出c=0或2,与0<c<1矛盾,………………………………………………………14分
所以直线AB与⊙P不能相切. …………………………………………………………15分
评讲建议:
此题主要考查直线与直线、直线与圆以及椭圆的相关知识,要求学生理解三角形外接圆圆心是三边中垂线的交点,从而大胆求出交点坐标,构造关于椭圆中a,b,c的齐次等式得离心率的范围.第二小题亦可以用平几的知识:圆的切割线定理,假设直线AB与⊙P相切,则有AB2=AF×AC,易由椭圆中a,b,c的关系推出矛盾.
17.(本小题满分15分)
口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:
甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,
否则算乙赢.
(Ⅰ)求甲赢且编号的和为6的事件发生的概率;
(Ⅱ)这种游戏规则公平吗?试说明理由.
解:(I)设“甲胜且两数字之和为6”为事件A,事件A包含的基本事件为
(1,5),(2,4),(3,3),(4,2),(5,1),共5个.……………………2分
又甲、乙二人取出的数字共有5×5=25(个)等可能的结果, ……………………4分
所以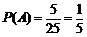 . ………………………………………………………………………6分
. ………………………………………………………………………6分
答:编号的和为6的概率为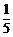 .…………………………………………………………………7分
.…………………………………………………………………7分
(Ⅱ)这种游戏规则不公平.……………………………………………………………………9分
设“甲胜”为事件B,“乙胜”为事件C, ……………………………………………10分
则甲胜即两数字之和为偶数所包含的基本事件数为13个:
(1,1),(1,3),(1,5),(2,2),(2,4),(3,1),(3,3),(3,5),
(4,2) ,(4,4),(5,1) ,(5,3),(5,5).
所以甲胜的概率P(B)=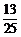 ,从而乙胜的概率P(C)=1-
,从而乙胜的概率P(C)=1-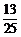 =
=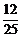 .…………14分
.…………14分
由于P(B)≠P(C),所以这种游戏规则不公平. ………………………………15分
评讲建议:
本题主要考查古典概率的计算及其相关知识,要求学生列举全面,书写规范.尤其注意此类问题的答题格式:设事件、说明概型、计算各基本事件种数、求值、作答.
引申:连续玩此游戏三次,若以D表示甲至少赢一次的事件,E表示乙至少赢两次的事件,试问D与E是否为互斥事件?为什么?(D与E不是互斥事件.因为事件D与E可以同时发生,如甲赢一次,乙赢两次的事件即符合题意;亦可分别求P(D)、P(E),由P(D)+ P(E)>1可得两者一互斥.)
16.(本小题满分14分)
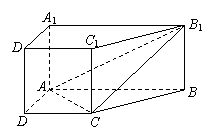
直棱柱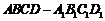 中,底面ABCD是直角梯形,
中,底面ABCD是直角梯形,
∠BAD=∠ADC=90°, .
.
(Ⅰ)求证:AC⊥平面BB1C1C;
(Ⅱ)在A1B1上是否存一点P,使得DP与平面BCB1与
平面ACB1都平行?证明你的结论.
证明:(Ⅰ) 直棱柱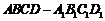 中,BB1⊥平面ABCD,
中,BB1⊥平面ABCD,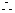 BB1⊥AC. ………………2分
BB1⊥AC. ………………2分
又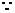 ∠BAD=∠ADC=90°,
∠BAD=∠ADC=90°, ,
,
∴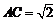 ,∠CAB=45°,∴
,∠CAB=45°,∴ ,
,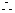 BC⊥AC.………………………………5分
BC⊥AC.………………………………5分
又 ,
,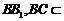 平面BB1C1C,
平面BB1C1C,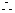 AC⊥平面BB1C1C. ………………7分
AC⊥平面BB1C1C. ………………7分
(Ⅱ)存在点P,P为A1B1的中点. ……………………………………………………………8分
证明:由P为A1B1的中点,有PB1‖AB,且PB1=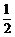 AB.……………………………………9分
AB.……………………………………9分
又∵DC‖AB,DC=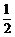 AB,
AB,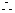 DC ∥PB1,且DC= PB1,
DC ∥PB1,且DC= PB1,
∴DC PB1为平行四边形,从而CB1∥DP.……………………………………………11分
又CB1 面ACB1,DP
面ACB1,DP 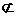 面ACB1,
面ACB1, DP‖面ACB1.………………………………13分
DP‖面ACB1.………………………………13分
同理,DP‖面BCB1.……………………………………………………………………14分
评讲建议:
本题主要考查线面平行、垂直的的判定和证明等相关知识,第一小题要引导学生挖掘直角梯形ABCD中BC⊥AC,第二小题,要求学生熟练掌握一个常用结论:若一直线与两相交平面相交,则这条直线一定与这两平面的交线平行;同时注意问题的逻辑要求和答题的规范性,这里只需要指出结论并验证其充分性即可,当然亦可以先探求结论,再证明之,这事实上证明了结论是充分且必要的.
变题:
求证:(1)A1B⊥B1D;(2)试在棱AB上确定一点E,使A1E∥平面ACD1,并说明理由.
15.(本小题满分14分)
在△ABC中,角A,B,C所对边分别为a,b,c,且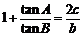 .
.
(Ⅰ)求角A;
(Ⅱ)若m ,n
,n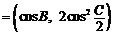 ,试求|m
,试求|m n|的最小值.
n|的最小值.
解:(Ⅰ) ,……………………………………………3分
,……………………………………………3分
即 ,
,
∴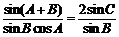 ,∴
,∴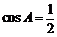 . ………………………………………………5分
. ………………………………………………5分
∵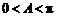 ,∴
,∴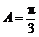 .………………………………………………………………7分
.………………………………………………………………7分
(Ⅱ)m n
n 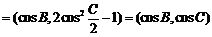 ,
,
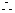 |m
|m n|
n|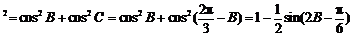 .…………10分
.…………10分
∵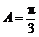 ,∴
,∴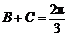 ,∴
,∴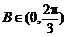 .
.
从而 .……………………………………………………………12分
.……………………………………………………………12分
∴当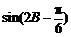 =1,即
=1,即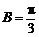 时,|m
时,|m n|
n| 取得最小值
取得最小值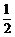 .……………………13分
.……………………13分
所以,|m n|
n|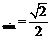 .………………………………………………………………14分
.………………………………………………………………14分
评讲建议:
 本题主要考查解三角形和向量的运算等相关知识,要求学生涉及三角形中三角恒等变换时,要从化角或化边的角度入手,合理运用正弦定理或余弦定理进行化简变形;在第二小题中,要强调多元问题的消元意识,进而转化为函数的最值问题,注意定义域的确定对结论的影响,并指明取最值时变量的取值.
本题主要考查解三角形和向量的运算等相关知识,要求学生涉及三角形中三角恒等变换时,要从化角或化边的角度入手,合理运用正弦定理或余弦定理进行化简变形;在第二小题中,要强调多元问题的消元意识,进而转化为函数的最值问题,注意定义域的确定对结论的影响,并指明取最值时变量的取值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com