
在下列个小题的横线上,写出相应的诗文名句或作家作品。(10分)
① ,思而不学则殆。 (《论语》)
② ,蜡炬成灰泪始干。 (李商隐《无题》)
③ 受任于败军之际, ,尔来二十又一年矣。(诸葛亮《 》)
④安得广厦千万间, ,大庇天下寒士俱欢颜。( 《茅屋为秋风所破歌》)
⑤蒹葭苍苍, 。所谓伊人, 。(《诗经·蒹葭》)
⑥剪不断,理还乱,是离愁, 。 (李煜《相见欢》)
⑦落红不是无情物, 。 (龚自珍《己亥杂诗》)
2.请根据要求填写古诗文名句 (8分)
(1) ____________________,悠然见南山。 (陶渊明《饮酒》)
(2) _____________________,随风直到夜郎西。(李白《闻王昌龄左迁龙标遥有此寄》)
(3)_____________________,东风无力百花残。 (李商隐《无题》)
(4) 马作的卢飞快,_____________________。 (辛弃疾《破阵子》)
(5)子日:“岁寒,_________________________________。” (《论语·子罕》)
(6)______________________________;处江湖之远则忧其君。 (范仲淹《岳阳楼记》)
(7)“时有落花至,远随流水香”这两句诗表现了落花积极进取的精神.但龚自珍《已亥杂诗》中的“__________________________,____________________________________”在境界上更胜一筹。
2.默写。(7分)
(1) ,身世浮沉雨打萍。 (2) ,恨别鸟惊心。
(3)何当共剪西窗烛, 。 (4)但愿人长久, 。
(5)无丝竹之乱耳, 。
(6)请写出古诗文中表现作者雄心壮志的两个名句:
8.默写。(每空1分,共9分)
(1) ,天涯若比邻。 (王勃《送杜少府之任蜀州》)
(2) ,月涌大江流。 (杜甫《旅夜书怀》)
(3)但愿人长久, 。(苏轼《水调歌头》)
(4)山重水复疑无路, 。(陆游《游山西村》)
(5) ,各领风骚数百年。(赵翼《论诗》)
(6)三人行, 。(《论语》)
(7)业精于勤荒于嬉, 。(韩愈《进学解》)
(8)为人处世要洁身自好、不媚世俗,应像“莲”那样“ , ”。(请用《爱莲说》中的名句填写)
1.用课文原句填空。(10分)
(1)采菊东篱下, 。(陶渊明《饮酒》)
(2) ,江人大荒流。(李白《渡荆门送别》)
(3) ,大庇天下寒士俱欢颜!(杜甫《茅屋为秋风所破歌》)
(4)忽如一夜春风来, 。(岑参《白雪歌送武判官归京》)
(5)人生自古谁无死? 。(文天祥《过零丁洋》)
(6)人有悲欢离合, ,此事古难全。(苏轼《水调歌头》)
(7)夕阳西下, 。(马致远《天净沙·秋思》)
(8)苔痕上阶绿, 。(刘禹锡《陋室铭》)
(9)《岳阳楼记》中的“ ; ”表现了“古仁人”在不同处境中都忧 国忧民的思想境界。
3.默写古诗文名句,并写出相应的作家、篇名。(10分)
①学而时习之,不亦说乎? ,不亦乐乎?(《<论语>八则》)
② ,长河落日圆。( 《使至塞上》)
③感时花溅泪, 。(杜甫《春望》)
④ ,却话巴山夜雨时。(李商隐《 》)
⑤ ,月如钩。寂寞梧桐深院锁清秋。(李煜《相见欢》)
⑥落红不是无情物, 。(龚自珍《己亥杂诗》)
⑦予独爱莲之 ,濯清涟而不妖……(周敦颐《爱莲说》)
⑧而或长烟一空,皓月千里, , ……(范仲淹《岳阳楼记》)
10.某单位一辆交通车载有8个职工从单位出发送他们下班回家,途中共有甲、乙、丙3个停车点,如果某停车点无人下车,那么该车在这个点就不停车.假设每个职工在每个停车点下车的可能性都是相等的,求下列事件的概率:
(1)该车在某停车点停车;
(2)停车的次数不少于2次;
(3)恰好停车2次.
解:将8个职工每一种下车的情况作为1个基本事件,那么共有38=6561(个)基本事件.
(1)记“该车在某停车点停车”为事件A,事件A发生说明在这个停车点有人下车,即至少有一人下车,这个事件包含的基本事件较复杂,于是我们考虑它的对立事件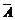 ,即“8个人都不在这个停车点下车,而在另外2个点中的任一个下车”.
,即“8个人都不在这个停车点下车,而在另外2个点中的任一个下车”.
∵P(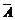 )=
)=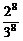 =
=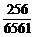 ,
,
∴P(A)=1-P(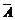 )=1-
)=1-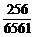 =
= .
.
(2)记“停车的次数不少于2次”为事件B,则“停车次数恰好1次”为事件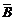 ,则P(B)=1-P(
,则P(B)=1-P(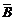 )=1-
)=1-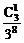 =1-
=1-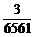 =
=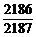 .
.
(3)记“恰好停车2次”为事件C,事件C发生就是8名职工在其中2个停车点下车,每个停车点至少有1人下车,所以该事件包含的基本事件数为C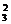 (C
(C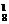 +C
+C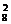 +C
+C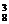 +…+C
+…+C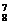 )=3×(28-2)=3×254,于是P(C)=
)=3×(28-2)=3×254,于是P(C)=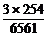 =
=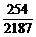 .
.
[探索题]袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为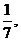 现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用
现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用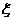 表示取球终止所需要的取球次数.
表示取球终止所需要的取球次数.
(I)求袋中原有的白球的个数;(II)求取球两次终止的概率;(III)求甲取到白球的概率.
解:(I)设袋中原有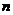 个白球,由题意知
个白球,由题意知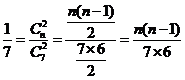
可得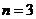 或
或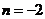 (舍去),即袋中原有3个白球。
(舍去),即袋中原有3个白球。
(II)记“取球两次终止” 的事件为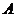 ,则
,则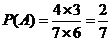 。
。
(III) 记“甲取到白球”的事件为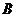 ,“第
,“第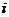 次取出的球是白球”的事件为
次取出的球是白球”的事件为 。
。
因为甲先取,所以甲只有可能在第1次,第3次取球和第5次取球,
∴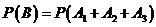 。因为事件
。因为事件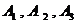 两两互斥,
两两互斥,
∴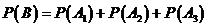
=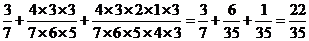
9.袋中有红、黄、白色球各一个,每次任取一个,有放回抽三次,计算下列事件的概率:
(1)三次颜色各不同;(2)三种颜色不全相同;(3)三次取出的球无红色或无黄色;
解:基本事件有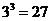 个,是等可能的,
个,是等可能的,
(1)记“三次颜色各不相同”为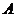 ,
,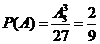 ;
;
(2)记“三种颜色不全相同”为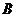 ,
, ;
;
(3)记“三次取出的球无红色或无黄色”为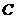 ,
,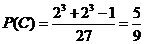 ;
;
8.某单位36人的血型类型是:A型12人,B型10人,AB型8人,O型6人.现从这36人中任选2人.
求:(1)两人同为A型血的概率;
(2)两人具有不相同血型的概率.
解:(1)P=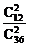 =
=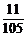 .
.
(2)考虑对立事件:两人同血型为事件A,
那么P(A)=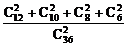 =
=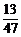 .
.
所以不同血型的概率为P=1-P(A)=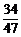 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com