2009直线运动

选择题

1(2009届山东实验中学高三模拟) 在2008北京奥运会中，牙买加选手博尔特是一公认的世界飞人，在男子100m决赛和男子200m决赛中分别以9.69s和19.30s的成绩破两项世界纪录，获得两枚金牌。关于他在这两次决赛中的运动情况，下列说法正确的是　　 (.C )

A．200m决赛中的位移是100m决赛的两倍

B．200m决赛中的平均速度约为10.36m/s

C．100m决赛中的平均速度约为10.32m/s

D．100m决赛中的最大速度约为20.64m/s

2.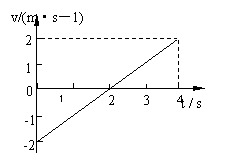(2009广东肇庆市一模)下列运动情况可能出现的是(ABD )

A.物体的加速度增大时，速度反而减小

B. 物体的速度为零时，加速度反而不为零

C.物理的加速度不为零且始终不变，速度也始终不变

D.物体的加速度逐渐减小，速度逐渐增大

17.(05全国卷Ⅰ23)原地起跳时,先屈腿下蹲,然后突然蹬地.从开始蹬地到离地是加速过程(视为匀加速),加速过程中重心上升的距离称为“加速距离”.离地后重心继续上升,在此过程中重心上升的最大距离称为“竖直高度”.现有下列数据：人原地上跳的“加速距离”d1=0.50 m,“竖直高度”h1=1.0 m;跳蚤原地上跳的“加速距离”d2=0.000 80 m,“竖直高度”h2=0.10 m.假想人具有与跳蚤相等的起跳加速度,而“加速距离”仍为0.50 m,则人跳的“竖直高度”是多少？　

答案　 62.5 m

解析　 用a表示跳蚤起跳的加速度,v表示离地时的速度,则对加速过程和离地后上升过程分别有　

v2=2ad2 　　　　　　　　　　　　　　　　　　　　　 　　　　　 ①

v2=2gh2 　　　　　　　　　　　　　　　　　　　　　　　　 　　②

若假想人具有和跳蚤相同的加速度a,令v1表示在这种假想下人离地时的速度,H表示与此相应的竖直高度,则对加速过程和离地后上升过程分别有　

v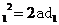　　　　　　　　　　　　　 　　　　　　　 　　 ③　

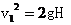　　　　　　　　　　　　　　　　　　　 　　 ④　

由以上各式可得

代入数值,得H=62.5 m

16．(07全国卷Ⅰ23)甲乙两运动员在训练交接棒的过程中发现：甲经短距离加速后能保持9 m/s 的速度跑完全

程;乙从起跑后到接棒前的运动是匀加速的.为了确定乙起跑的时机,需在接力区前适当的位置设置标记.在某

次练习中,甲在接力区前s0=13.5 m 处作了标记,并以v=9 m/s 的速度跑到此标记时向乙发出起跑口令.乙在

接力区的前端听到口令时起跑,并恰好在速度达到与甲相同时被甲追上,完成交接棒.已知接力区的长度为

L=20 m.求：

(1)此次练习中乙在接棒前的加速度a.　

(2)在完成交接棒时乙离接力区末端的距离.　

答案　 (1)3 m/s2　　 (2)6.5 m?　

解析　 (1)在甲发出口令后,甲、乙达到共同速度所用时间为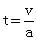　　　　 ①

设在这段时间内甲、乙的位移分别为s1和s2,则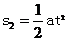　　　　　　　 ②

s1=vt　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ③

s1=s2+s0　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　④

联立①、②、③、④式解得: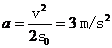

(2)在这段时间内,乙在接力区的位移为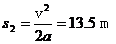

完成交接棒时,乙与接力区末端的距离为L-s2=20 m-13.5 m=6.5 m

15.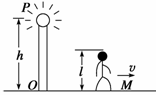(04广西14)一路灯距地面的高度为h,身高为l的人以速度v匀速行走,

如图所示.

(1)试证明人的头顶的影子做匀速运动.

(2)求人影的长度随时间的变化率.

答案　 (1)见解析　 (2)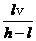

解析　 (1)设t=0时刻,人位于路灯的正下方O处,在时刻t,人走到S处,根据题意有OS=vt　　　 ①

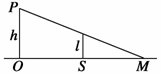过路灯P和人头顶的直线与地面的交点M为t时刻人头顶影子的位置,如图所示,OM为人头顶影子到O点的距离,由几何关系,有　

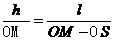　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　②

联立①②得OM=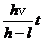　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ③

因OM与时间t成正比,故人头顶的影子做匀速运动.

(2)由图可知,在时刻t,人影的长度为SM,由几何关系,有SM=OM-OS　　　　　　　　　　　　 ④

由①③④式得SM=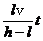

可见影长SM与时间t成正比,所以影长随时间的变化率为k=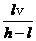

14.(06上海20)要求摩托车由静止开始在尽量短的时间内走完一段直道,然后驶入一段半圆形的弯道,但在弯道上行驶时车速不能太快,以免因离心作用而偏出车道.求摩托车在直道上行驶所用的最短时间.有关数据见表格.

某同学是这样解的:要使摩托车所用时间最短,应先由静止加速到最大速度v1=40 m/s,然后再减速到

v2=20 m/s,t1=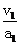=…;t2=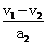=…;t=t1+t2　

你认为这位同学的解法是否合理?若合理,请完成计算;若不合理,请说明理由,并用你自己的方法算出正确结果.

答案　　 不合理　 11 s

解析　 上述解法不合理,因为加速时间t1=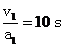,减速时间t2=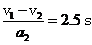,所以加速距离s1=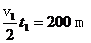,减速距离s2=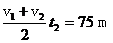,又因s1+s2>s,故解法不合理.　

摩托车先以a1=4 m/s2加速到最大速度vm,又以加速度a2=8 m/s2减速到v 2=20 m/s,恰完成直道s=218 m的距离,这样用时最短.则:加速距离s1=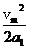,减速距离s2=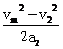

所以: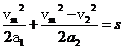

代入数据得:vm =36 m/s

加速时间t1=

减速时间t2=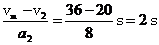

故最短时间t=t1+t2=9　s+2 s=11 s

13.(06全国卷Ⅰ23)天空有近似等高的浓云层.为了测量云层的高度,在水平地面上与观测者的距离 d =3.0 km处进行一次爆炸,观测者听到由空气直接传来的爆炸声和由云层反射来的爆炸声时间上相差Δt =6.0 s.试估算云层下表面的高度.已知空气中的声速v　=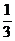 km/s.

答案　 2.0×103 m

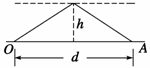解析　 如右图所示, A表示爆炸处,O表示观测者所在处,h表示地面与云层下表

面的高度.用t1表示爆炸声直接传到O处所经时间,则有　

d=vt1　　　　　　　　　　　　　　　　　　　　　　　　　　 ①　

用t2表示爆炸声经云层反射到达O处所经时间,因为入射角等于反射角,故有　

　　　　　　　　　　　　　　　　　　　 ②　

已知 t2-t1=Δt　　　　　　　　　　　　　　　　　　　　　　 ③　

联立①、②、③式,可得

h=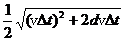

代入数据得h=2.0×103 m

12.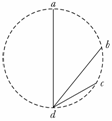(04全国卷Ⅰ15)如图所示, ad、bd、cd是竖直面内三根固定的光滑细杆,a、b、c、d

位于同一圆周上,a点为圆周的最高点,d点为最低点.每根杆上都套着一个小滑环(圆

中未画出),三个滑环分别从a、b、c处释放(初速为0),用t1、t2、t3依次表示各滑

环到达d所用的时间,则　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )　

? A.t1＜t2＜t3　　　　　　　　 B. t1＞t2＞t3?　　　 C.t3＞t1＞t2　　　　　　　 ? D.t1=t2=t3

答案?D

解析　 设圆环直径为d,杆与水平面的夹角为α,则杆长可表示为d sin α,下滑加速度a=g sin α.据

s=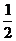at2知d sin α=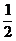gsinα·t2　

由于t与α无关,故下滑时间相同.

11.(04广东9)一杂技演员,用一只手抛球、接球.他每隔0.40 s抛出一个球,接到球便立即把球抛出.已知除抛、接球的时刻外,空中总有4个球,将球的运动近似看作是竖直方向的运动,球到达的最大高度是(高度从抛球点算起,取g=10 m/s2)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ( 　　)

A.1.6 m　　　　 B.2.4 m　　　　 C.3.2 m　　　　 D.4.0 m

答案?C

解析　 假设某时刻刚好有一球A抛出手,由题意知空中有4个球,过0.4 s就有一个球落在手中,那么A球过1.6 s落入手中,A球上升到最高点只需0.8 s,.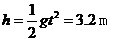

10.(06上海13)如图所示,一足够长的固定斜面与水平面的夹角为37°,物体A

以初速度v1从斜面顶端水平抛出,物体B在斜面上距顶端L=15 m处同时以

速度v2沿斜面向下匀速运动,经历时间t物体A和B在斜面上相遇,则下列

各组速度和时间中满足条件的是(sin 37°=0.6,cos 37°=0.8,g=10 m/s2)(　　 )　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　

A.v1=16 m/s,v2=15 m/s,t=3 s?　　　　　 B.v1=16 m/s,v2=16 m/s,t=2 s

C.v1=20 m/s,v2=20 m/s,t=3 s?　　　　　 D.v1=20 m/s,v2=16 m/s,t=2 s

答案?C

解析　 设平抛物体落到斜面上的时间为t,则tan37°=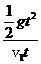,t=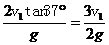,时间t内平抛物体的水平

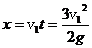位移:,竖直位移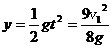.时间t内B物体的位移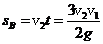

A、B两物体相碰时,满足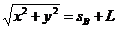

整理得: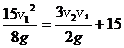.把各选项值代入得:v1=20 m/s,v2=20 m/s,t=3 s符合上式,故C选项正确.

0.34 km/s

∴s=vt=0.34t≈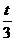km,显然声速加倍后不再成立.