
12.已知点G为△ABC的重心,过G作直线与AB、AC两边分别交于M、N两点,且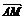 =x
=x ,
,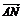 =y
=y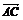 ,
,
求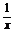 +
+ 的值.
的值.
解 根据题意G为三角形的重心,
故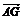 =
=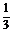 (
( +
+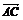 ),
),
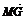 =
=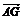 -
-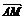 =
=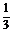 (
( +
+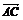 )-x
)-x
=(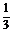 -x)
-x) +
+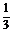
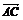 ,
,
 =
=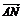 -
-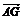 =y
=y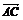 -
-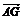
=y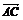 -
-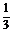 (
( +
+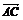 )
)
=(y-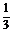 )
)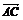 -
-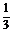
 ,
,
由于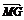 与
与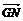 共线,根据共线向量基本定理知
共线,根据共线向量基本定理知
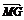 =
=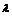
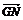
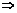 (
(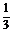 -x)
-x) +
+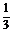
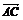
=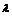
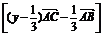 ,
,
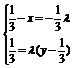
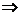
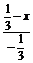 =
=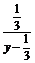
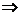 x+y-3xy=0两边同除以xy得
x+y-3xy=0两边同除以xy得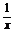 +
+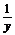 =3.
=3.
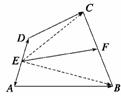
11.已知:任意四边形ABCD中,E、F分别是AD、BC的中点,求证: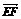 =
=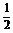 (
( +
+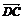 ).
).
证明 方法一 如图,
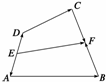 ∵E、F分别是AD、BC的中点,
∵E、F分别是AD、BC的中点,
∴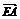 +
+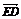 =0,
=0,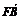 +
+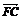 =0,
=0,
又∵ +
+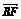 +
+ +
+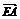 =0,
=0,
∴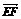 =
= +
+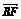 +
+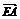 ①
①
同理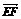 =
=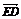 +
+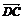 +
+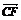 ②
②
由①+②得,
2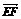 =
= +
+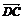 +(
+(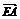 +
+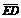 )+(
)+(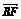 +
+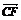 )=
)= +
+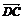 .
.
∴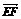 =
=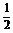 (
( +
+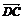 ).
).
 方法二 连结
方法二 连结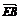 ,
, ,
,
则 =
=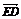 +
+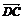 ,
,
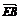 =
=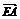 +
+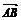 ,
,
∴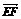 =
=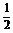 (
( +
+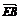 )
)
=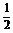 (
(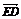 +
+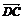 +
+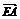 +
+ )
)
=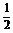 (
( +
+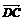 ).
).
10.如图所示,在△ABC中,D、F分别是BC、AC的中点, =
=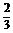
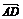 ,
, =a,
=a,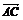 =b.
=b.
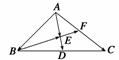 (1)用a、b表示向量
(1)用a、b表示向量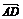 、
、 、
、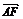 、
、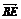 、
、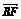 ;
;
(2)求证:B、E、F三点共线.
(1)解 延长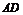 到G,使
到G,使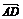 =
=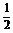
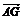 ,
,
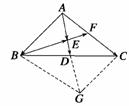
 连接BG、CG,得到 ABGC,
连接BG、CG,得到 ABGC,
所以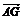 =a+b,
=a+b,
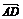 =
=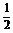
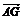 =
=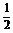 (a+b),
(a+b),
 =
=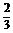
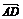 =
=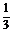 (a+b).
(a+b).
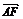 =
=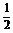
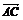 =
=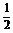 b,
b,
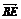 =
= -
- =
=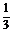 (a+b)-a=
(a+b)-a=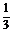 (b-2a).
(b-2a).
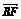 =
=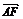 -
- =
=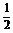 b-a=
b-a=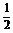 (b-2a).
(b-2a).
(2)证明 由(1)可知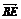 =
=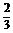
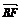 ,所以B、E、F三点共线.
,所以B、E、F三点共线.
9.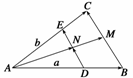 如图所示,△ABC中,
如图所示,△ABC中,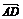 =
=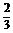
 ,DE∥BC交AC于E,AM是BC边上中线,交DE于N.设
,DE∥BC交AC于E,AM是BC边上中线,交DE于N.设 =a,
=a,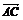 =b,用a,b分别表示向量
=b,用a,b分别表示向量 ,
,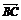 ,
,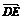 ,
,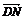 ,
,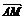 ,
,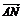 .
.
解 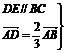
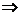
 =
=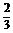
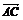 =
=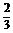 b.
b.
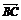 =
=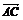 -
- =b-a.
=b-a.
由△ADE∽△ABC,得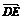 =
=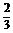
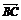 =
=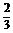 (b-a).
(b-a).
由AM是△ABC的中线,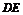 ∥BC,得
∥BC,得
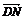 =
=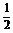
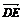 =
=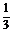 (b-a).
(b-a).
而且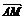 =
= +
+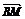 =a+
=a+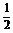
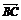 =a+
=a+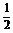 (b-a)
(b-a)
=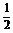 (a+b).
(a+b).
|


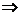
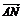 =
=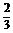
 =
=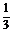 (a+b).
(a+b).8.在△ABC中,已知D是AB边上一点,若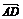 =2
=2 ,
,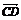 =
=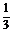
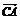 +
+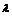
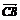 ,则
,则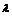 =
.
=
.
答案 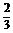
7.在△ABC中,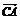 =a,
=a,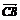 =b,M是CB的中点,N是AB的中点,且CN、AM交于点P,则
=b,M是CB的中点,N是AB的中点,且CN、AM交于点P,则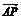 可用a、b表示为
.
可用a、b表示为
.
答案 -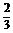 a+
a+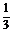 b
b
6.已知平面内有一点P及一个△ABC,若 +
+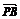 +
+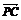 =
= ,则点P在线段
上.
,则点P在线段
上.
答案 AC
5.设 =x
=x +y
+y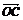 ,且A、B、C三点共线(该直线不过端点O),则x+y=
.
,且A、B、C三点共线(该直线不过端点O),则x+y=
.
答案 1
4.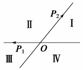 如图所示,平面内的两条相交直线OP1和OP2将该平面
如图所示,平面内的两条相交直线OP1和OP2将该平面
分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ(不包括边界).若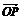
=a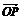 1+b
1+b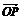 2,且点P落在第Ⅲ部分,则实数a,b满足
2,且点P落在第Ⅲ部分,则实数a,b满足
a 0,b 0.(用“>”,“<”或“=”填空)
答案 > <
3.若 =3e1,
=3e1,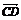 =-5e1,且|
=-5e1,且|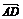 |=|
|=|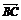 |,则四边形ABCD是
.
|,则四边形ABCD是
.
答案 等腰梯形
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com